向量

基本概念

数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。其主要特性有

1. 元素类型相同
   • 元素顺序的存储在连续的存储空间中，每个元素有唯一的索引值
   • 使用常数作为向量长度
2. 读写元素很方便，通过下标即可指定位置
   • 只要确定了首地址，线性表中任意数据元素都可以随机访问

数组元素地址计算公式为：

顺序表类定义

class Array:public List<T>{
	private:
		T* list;
		int maxSize; //向量实际的内存空间
		int curLen; //向量当前长度，这个值小于maxSize，要预留一部分存储空间，放置频繁的内存开销
		int position;
	public:
		Array(const int size){
			maxSize = size;
			list = new T[maxSize];
			curLen = position = 0;
		}
		~MyList(){
			delete []list;
			list = nullptr;
		}
		void clear(){
			delete []list;
			list = nullptr;
			position = 0;
			list = new T[maxSize];
		}
		int length();
		bool append(const T value);
		bool insert(const int p, const T value);
		bool remove(const int p);
		bool setValue(const int p, const T value);
		bool getValue(const int p, T& value);
		bool getPos(int &p, const T value);
}

顺序表上的运算

• 插入运算

template<class T>
bool Array<T>::insert(const int p, const T value){
	if(curLen >= maxSize){
		//重新申请空间
		//或者报错
		return false;
	}
	if(p<0 || p>=curLen){
		return false;
	}
	for(int i=curLen;i>p;i--){
		list[i] = list[i-1];
	}
	list[p] = value;
	curLen ++;

	return true;
}

上面代码可以看出，数组的插入运算效率很低。其原因是由于数据是连续存储的，每进行一次插入，需要移动n-i个元素。我们可以来分析一下其时间复杂度。如果在末尾查入，则效率很高，时间复杂度为O(1)；如果是在数组头部插入，则是最差情况，时间复杂度是O(n)。我们假设在数组中每个位置插入数据的概率相同，那么平均的时间复杂度为(1+2+3+...+n)/n = O(n)。

对于插入操作，有一个巧妙的算法，如果我们不关心数组中元素的位置关系，只把它当做集合使用，则插入操作可以做到O(1)的时间复杂，其思路如下：

	x
	|
a b c d e
a b x d e c

上面例子中，假设数组a[10] 中存储了如下 5 个元素：a，b，c，d，e。我们现在需要将元素x插入到第3个位置。我们只需要将c放入到a[5，将 a[2] 赋值为x即可。最后，数组中的元素如下:a，b，x，d，e，c。

• 删除运算

template<class T>
bool Array<T>::delete(const int p){
	if(curLen == 0){
		return false;
	}
	if(p == 0 || p>=curLen){
		return false;
	}
	for(int i=p; i<curLen-1; i++){
		list[i] = list[i+1];
	}
	curLen--;

	return true;
}

删除操作和插入类似，也需要搬移数据，每删除一个数据，需要移动n-i-1个元素，平均时间复杂度也为O(n)。如果可以对删除操作进行批处理，效率则会提高很多，例如有些场景，我们不需要对每次删除操作都进行数据搬移，可以累积多次后进行一次批量删除。

我们看一个例子，数组a[10]中存储了8个元素a，b，c，d，e，f，g，h。现在，我们要依次删除a，b，c 三个元素。

a b c | d e f g h

为了避免d，e，f，g，h这几个数据会被搬移三次，我们可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，我们再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。

数组的应用

数组问题是面试中经常出现的问题，本节会分析一些LeetCode中常见的数组高频题，并总结使用数组解题的一般技巧。

去重问题

去重问题顾名思义，是指一个数组中去掉重复的元素。这个问题看似简单，但实际上需要考虑很多种情况，比如

1. 数组是否有序
2. 是否可以使用额外的辅助空间
3. 是否要求操作是inplace的，即去重操作需要在原数组内完成
4. 如果数组中有重复的元素有多个，是保留1个还是n个

针对不同的场景，其解法也不尽相同，有的解法效率高，占用空间也少，有的效率低并且也浪费空间。

首先，我们来看第一个问题，如何对一个有序数组去重，详细的问题描述可以参考LeetCode26。

如果数组有序，我们可以使用读写双指针进行遍历，读指针移动，写指针待命，当读指针和写指针内容不同时，写指针+1，修改内容为读指针指向的数据，代码如下:

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if(nums.size() <= 1 ){
            return nums.size();
        }
		//two pointers
    	int write = 1;
        int read = 1;
        while(read < nums.size()){
            if(nums[read] != nums[write-1]){    
                nums[write++] = nums[read];
            }
            read++;
        } 
		return write;
    }
};

这个题目有一个follow up，是说有序数组中，每个重复元素最多只保留2个，求去重后的数组。变种后的题目实际上思路和上面代码是一致的，判断重复的条件有所变化

int write = 2;
int read = 2;
while(read < nums.size()){
	if(nums[read] != nums[write-2]){    
		nums[write++] = nums[read];
	}
	read++;
} 

上述算法的时间复杂度均为O(n)。对于无序数组的去重则需要在双指针的基础上，增加一个辅助集合（通常是set）保存非重复元素，将判重条件修改为查看set是否存在即可，这种方式的时间复杂度同样为O(n)，但是引入了空间复杂度O(n)。如果不允许使用额外空间，则只能先排序后再排重，时间复杂度为O(log(n))。

• 26. Remove Duplicates from Sorted Array
• 80. Remove Duplicates from Sorted Array II

子数组最优解问题

最优化问题通常是寻找数组中的一个连续子数组或者一个不连续的子序列，使其满足某种条件（注意，不能排序，需要保持原序列顺序）。解这类问题通常有三种办法：

1. 如果求连续子数组考虑使用滑动窗口
2. Kadane算法
3. 动态规划

我们先看一个使用Kadane算法的例子，原题是LeetCode中53. Maximum Subarray。题意是说找到数组中的一个subarray，使和最大，其中subarray的长度可以为1。

这个题是求解一个subarray，因此是求一个连续的区间，按照上面给出的思路，我们可以首先考虑使用滑动窗口，针对这道题，使用滑动窗口就相当于使用暴力求解，思路为枚举出所有的subarray然后求和，这种方式需要两层循环，时间复杂度为O(n^2)。

kadane算法的思路是遍历数组中的每个元素，以该元素结尾的最优subarray的和的计算公式为dp[i] = max(nums[i],dp[i-1]+nums[i])，意思是这个subarray要么是自己(例如前面都是负数，自己是正数)，要么是i-1位置的最大和subarray加上自己（比如前面都是正数，自己也是正数）。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size(),0);
        dp[0] = nums[0];
        int maxsum = dp[0];
        for(int i=1;i<nums.size();i++){
            dp[i] = max(nums[i],dp[i-1]+nums[i]);
            maxsum = max(maxsum,dp[i]);
        }
        return maxsum;
    }
};

使用Kadane算法，时间复杂度降低到O(n)。这个问题通常有一个follow up的问题，即如果将问题变为Maximum Subsequence，该怎么解

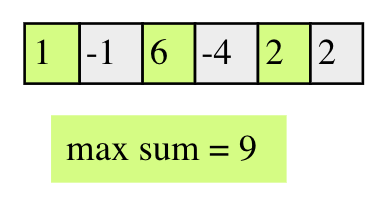
如上图中的解是一组不连续的序列，例如右图中的解我们不能选10和14，因为它们是连续的。虽然是求子序列，我们仍然可以使用kadane的思路，但是判断和最大的条件需要修改。对于数组中的每个元素，该元素位置的最优子序列的条件是：max(dp[i-2]+nums[i], dp[i-1])。即如果包含自己，那么它一定是和i-2位置的最优子序列和最大，如果不包含自己，则返回前i-1位置的最优子序列。

注意，上述算法是从i=2开始，因此我们的dp数组需要有两个初始值dp[0],dp[1]

dp[0] = arr[0];
dp[1] = max(dp[0],arr[1]);

以上面左图为例，遍历完成后dp序列的状态如下，由于dp序列的递增性，我们只要返回数组末尾即可。

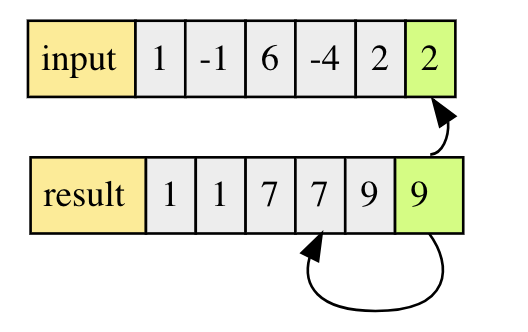
int find_max_sum_nonadjacent(vector<int>& a) {
 if(a.size() == 0){
	 reutrn 0;
 }
 if(a.size() == 1){
	 return a[0];
 }
 //维护一个dp序列
  vector<int> dp(a.size(),0);
  dp[0] = a[0];
  dp[1] = std::max(dp[0],a[1]);
  for(int i=2;i<a.size();i++){
    dp[i] = max(dp[i-1],a[i]+dp[i-2]);
  }
  return dp.back();
}

• 53. Maximum Subarray

K-Sum问题

K Sum问题是数组中的经典问题了，其核心的问题为如何在一个数组中找到若干个数，使它们的和为k。根据这几个数之间的位置关系，又可以衍生出两个变种，一个是求连续的子数组和为k，另一个是求不连续的序列，使其和为k。

解这类问题的方法有很多种，可以归为下面几种：

1. 对于非连续的元素可以考虑使用
   • 先排序后双指针碰撞
   • 使用hashmap做索引
   • 将问题转化为k-1 sum， 比如3sum可转化为for循环+two sum
2. 如果要求数据是连续的，则可以考虑使用
   • 双指针滑动窗口 + hashmap
   • 暴利枚举

关于Two Sum， Three Sum的问题解法都很经典，不做过多介绍。这里介绍一道LeetCode中第560题Subarray Sum Equals K的解法，这种解法相对巧妙，不太容易想到，具有一定的启发意义。该问题的描述为：

给定一个数组，求解所有数组中和为k的subarray的数量。

我们先来分析一下问题，题目是找出所有满足条件的subarray的数量，由于是subarray，因此数据是连续的，考虑使用滑动窗口或者暴利枚举。先看比较直观的枚举法，枚举法就是令i从0到size()-1，依次遍历所有的subarray，并找出符合条件的解

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for(int i=0;i<nums.size();i++){
            int sum = 0;
            for(int j=i;j<nums.size();j++){
                sum += nums[j];
                if(sum==k){
                    count += 1;
                }
            }
        }
        return count;
    }
};

上述枚举方法时间复杂度为O(n^2)，其问题在于第二层循环中存在大量的重复计算，比如i=0时，我们计算过一遍j=0到n-1的sum0，当i=1时，我们又计算了一遍j=1到n-1的sum1，而sum0和sum1之间有这样的关系：sum1 = sum0 - a[0]。因此我们的优化方向是尽量避免重复计算，我们可以先将数组中每个元素位置的sum值先提前计算好，保存在数组里，比如有数组：

vector<int> arr = [1,-1,0,2];

可以先计算出每个位置的prefixSum：

vector<int> prefixSum = [1,0,0,2];

现在假设k=2，显然从prefixSum数组中可以看到最后一个值为2，因此[1,-1,0,2]是一组解，subarray的范围是从[0,3]。除了这个解之外，还能看到有两组解，分别为[2]本身，[0,2]，如何找到这些解呢？也可以通过prefixSum数组：

prefixSum[i] - prefixSum[x] = k; // x>=0 && x<i

接下来我们只要找到一个小于i的x位置，并且满足prefixSum[x] = prefixSum[i] - k即可，由于可能有0的存在，这样的x可能有多个，如上面例子中，当i=3时，prefixSum[3]=2，此时我们需要找到x使prefixSum[x] = 2-k = 0，显然x=1和x=2均是满足条件的解，这也恰好对应于prefixSum中的index值。给出实现代码如下：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        vector<int> prefix;
        int sum = 0;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
            prefix.push_back(sum);
        }
        int ans = 0;
        unordered_map<int,int> um;
        for(int i=0; i<nums.size();i++){
            int prefixSum = prefix[i];
            if(prefixSum == k){
                ans+=1;
            }
            int target = prefixSum-k;
            if(um.count(target)){
                ans+=um[target];
            }
            um[prefixSum]++;
        }
        return ans;
    }
};

使用prefixSum的方法，复杂度从O(n^2)降到了O(n)。其它关于KSum的问题：

• 1. Two Sum
• 15. 3Sum
• 16. 3Sum Closest
• 18. 4Sum
• 560. Subarray Sum Equals K
• 209. Minimum Size Subarray Sum
• 325. Maximum Size Subarray Sum Equals k

滑动窗口问题

滑动窗口问题也是数组相关的经典问题，并且经常和字符串问题一起出现。根据窗口类型的不同可分为固定窗口和非固定窗口，根据求解条件不同，又可分为substring和subsequence等，对于固定窗口的非字符串问题，可以使用Balanced BST，我们稍后会看一道例题。对于字符串的滑动窗口问题，将会在后面介绍字符串时再做介绍。

• 239. Sliding Window Maximum
• 480. Sliding Window Median
• 727. Minimum Window Subsequence

Resources

• CS106B-Stanford-YouTube
• Algorithms-Stanford-Cousera
• 算法与数据结构-1-北大-Cousera
• 算法与数据结构-2-北大-Cousera
• 算法与数据结构-1-清华-EDX
• 算法与数据结构-2-清华-EDX
• 算法设计与分析-1-北大-Cousera
• 算法设计与分析-2-北大-EDX