首页 | Home
博客 | Blog
关于 | About

栈与队列

Posted on | In DataStructure

栈

栈的实现方式

  • 顺序栈（Array-based Stack）
    • 使用向量实现，本质上是顺序表的简化版
    • 向量尾部可作为栈顶
  • 链式栈（Linked Stack）
    • 使用单链表方式存储
    • 其中指针的方向是从栈顶向下链接
      // 入栈操作的链式实现
  bool lnksStack<T>:: push(const T item) {
      Link<T>* tmp = new Link<T>(item, top);
      top = tmp;
      size++;
      return true;
  } 
  Link(const T info, Link* nextValue) {// 具有两个参数的Link构造函数
      data = info;
      next = nextValue;
  }
  • 顺序栈和链式栈的比较
    • 时间效率
      • 所有操作都只需要常数时间
      • 顺序栈和链式栈在时间效率上难分伯仲
    • 空间效率
      • 顺序栈需要一个固定长度
      • 链式栈长度可变，但增加结构开销
    • 实际应用中，顺序栈比链式栈用的更广泛
      • 顺序栈容易根据栈顶位置，进行相对位移，快速定位并读取栈内部的元素
      • 顺序栈读取内部元素时间为O(1),链式栈需要沿着栈顶指针游走，显然慢些，读取第k个元素需要的时间为O(k)。
      • 一般来说，栈不允许“读取内部元素”，只能在栈顶操作

计算表达式的值

  • 表达式的递归定义
    • 基本符号集合：{0，1，2，3，... ，9，+，-，*，/,(,)}
    • 语法成分集合: {<表达式>,<项>,<因子>,<常数>,<数字>}
  • 中缀表达式 23+(34*45)/(5+6+7)
    • 运算符在中间，需要括号改变优先级
    • 中缀表达式求值： 二叉树的中序遍历
    • 语法公式（巴克斯范式）：
  • 后缀表达式 23 34 45 * 56 + 7 + / +
    • 又称逆波兰表达式
    • 运算符在后面，不需要括号
    • 后缀表达式求值
      • 二叉树的后序遍历
      • 使用栈
        • 当遇到一个操作数，入栈
        • 当遇到一个运算符，从栈中两次取出栈顶，按照运算符对这两个操作数进行计算，然后将结果入栈

队列

  • 先进先出
    • 限制访问点的线性表
      • 按照到达的顺序来释放元素
      • 所有的插入在表的一端进行，所有的删除在表的另一端进行
  • 主要元素
    • 队头-front
    • 队尾-rear
  • 抽象数据类型
template <class T> 
class Queue {
public: // 队列的运算集
 	void clear(); // 变为空队列
 	bool enQueue(const T item);// 将item插入队尾，成功则返回真，否则返回假
 	bool deQueue(T & item) ;// 返回队头元素并将其从队列中删除，成功则返回真
 	bool getFront(T & item); // 返回队头元素，但不删除，成功则返回真
 	bool isEmpty(); // 返回真，若队列已空
 	bool isFull(); // 返回真，若队列已满
};

实现方式

  • 顺序队列
    • 使用线性表做环形表示，空间提前分配好
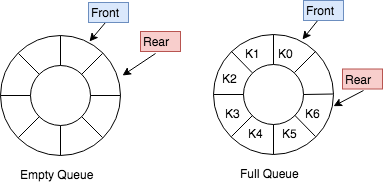
    • 维护front和rear做队头，队尾的游标
      • 空队列rear在front前面
      • 插入删除时间复杂度为O(1)

template <class Elem> 
class Aqueue : public Queue<Elem> {
	private:
 		int size; // 队列的最大容量
 		int front; // 队首元素指针
 		int rear; // 队尾元素指针
 		Elem *listArray; // 存储元素的数组
	public:
 		AQueue(int sz=DefaultListSize) {// 让存储元素的数组多预留一个空位
 			size = sz+1; // size数组长，sz队列最大长度
 			rear = 0; front = 1; // 也可以rear=-1; front=0
 			listArray = new Elem[size];
 		}
 		~AQueue() { delete [] listArray; }
 		void clear() { front = rear+1; } 
		int length() { reutrn (rear + 1 -front)%size; }
  • 入队
    • 在队尾插入，移动rear指针
      bool enqueue(const Elem& it){
      if(((rear+2)%size) == front){
          return false;
      }else{
          rear = (rear+1)%size;
          listArray[rear] = it;
          return true;
      }
  }
  • 出队
    • 依靠移动front指针，不进行delete元素的操作
      bool dequeue(Elem& it){
      if(length() == 0 ){
          return false;
      }
      it = listArray[front];
      front = (front+1)%size;
      return true;
  }
  • 链式队列
    • 用单链表方式存储，队列每个元素对于链表中的一个节点
    • 插入时间复杂度为O(1)

顺序队列和链式队列比较

  • 顺序队列
    • 固定存储空间
  • 链式队列
    • 可以满足大小无法估计的情况

  • 都不允许访问队列内部元素

  • 环形队列
    • 线性表在部分元素出队后会造成空间的浪费，解决这个问题，引入环形队列，它是一个首尾相连的FIFO的数据结构，采用数组的线性空间,数据组织简单。能很快知道队列是否满为空。
    • 插入时间复杂度为O(1)

队列与栈的经典问题

表达式求值

如前文所述，栈的一个应用是计算表达式的值，这里说的表达式是简单的加减乘除四则运算，其求值过程可分为两步，第一步为将中缀表达式转为后缀表达式，第二步是对后缀表达式进行求值。中缀转后缀的规则如下：

  1. 如果当前是数字，向后遍历直到遇到符号，输出数字
  2. 如果当前是(，直接入栈
  3. 如果当前是)，弹出栈中所有符号并输出，直到遇到(，弹出(
  4. 如果当前是+,-,*,/，根据优先级入栈
    • 如果当前符号优先级>栈顶元素，直接入栈
    • 如果当前符号优先级<=栈顶个元素，弹出栈顶元素，直到遇到(或者优先级更高的元素
vector<string> infix2postfix(string& postfix){
	vector<string> postfix;
	stack<char> stk;
	int i = 0;
	string num = "";
	while(i<postfix.size()){
		char c = postfix[i];
		if( isspace(c) ){
			i++;
			continue;
		}else if( isdigit(c) ){
			do{
				num+=c;
				i++;
				c = char[i];
			}while(isdigit(c));
			postfix.push_back(num);
			num = "";
			continue;
		}else if( c == '('){
			stk.push_back(c);
		}else if( c== ')' ){
			while(!stk.empty() && stk.top()!='('){
				postfix.push_back(string(1,stk.top()));
				stk.pop();
			}
			//pop ')'
			stk.pop();
		}else if( isoperator(c) ){
			while(!stk.empty() && level(c) <= level(stk.top())){
				postfix.push_back(string(1,stk.top()));
				stk.pop();
			}
			stk.push(c);
		}
		i++
	}
	//输出栈中符号
	while(!stk.emtpy()){
		postfix.push_back(string(1,stk.top()));
		stk.pop();
	}
	return postfix;
}

第二步是对后缀表达式进行求值，求值的算法前文已提到，这里不再赘述，代码如下

int calculate(string& infix){
	vector<string> postfix = infix2postfix(infix);
	stack<long> stk;
	int sum=0;
	for(auto &s : postfix){
		if(isoperator(s)){
			long x = stk.top();
			stk.pop();
			long y = stk.top();
			stk.pop();
			if(s == "+"){
				stk.push(x+y);
			}else if(s =="-"){
				stk.push(y-x);
			}else if(s =="*"){
				stk.push(x*y);
			}else if(s == "/"){
				stk.push(y/x);
			}
		}else{
			stk.push(stol(s));
		}
	}
	int sum = 0;
	while(!stk.empty()){
		sum += stk.top();
		stk.pop();
	}
	return sum;
}

Resources