字符串

字符串

• 字符串，特殊的线性表，即元素为字符的线性表
• n(≥0) 个字符的有限序列n≥1时，一般记作S: "c0c1c2...cn-1"
  • S 是串名字
  • "c0c1c2...cn-1"是串值
  • ci是串中的字符
    • N 是串长（串的长度）：一个字符串所包含的字符个数
    • 空串：长度为零的串，它不包含任何字符内容
• 子串
  • 假设s1,s2 是两个串：s1 = a0a1a2…an-1,s2 = b0b1b2…bm-1,其中 0 ≤ m ≤ n, 若存整数i (0 ≤ i ≤n-m)，使得 b(j) = a(i+j), j =0,1,…,m-1同时成立，则称串s2是串s1的子串,s1为串s2的主串，或称s1包含串s2
  • 特殊子串 – 空串是任意串的子串 – 任意串S都是S本身的子串 – 真子串：非空且不为自身的子串
• String 类
  • 内部封装了 C 字符串 API

字符串的特征向量

设模式p由m个字符组成，记为 p=p(0)p(1)...p(m-1)，令特征向量N用来表示模式P的字符分布特征，简称N向量由m个特征数n(0)...n(m-1)整数组成，记为 N=n(0)n(1)...n(m-1),N也称为 next 数组，每个n(j)对应 next 数组中的元素next[j]

• 字符串的特征向量的构造方法

设P第j个位置的特征数n(j)，首尾串最长的k。 则首串为： p(0)p(1)...p(k-2)p(k-1)；尾串为： p(j-k)p(j-k+1)...p(j-2)p(j-1)。特征向量next[j]为

即next[j]为长度为j的子串的前(j-1)个字符中最长的首尾真子串长度k。假设模式串P为aaaabaaaac，则特征向量N(next[j])的值为：

P = a  a  a  a  b  a  a  a  a  c
N = -1 0  1  2  x  0  1  2  3  4
              (x=3)

模式匹配

• 模式匹配（pattern matching）

  • 目标对象 T（字符串）
  • 模式 P（字符串）

• 给定模式 P，在目标字符串 T 中搜索与 P 模式匹配的子串，并返回第一个匹配串首字符的位置

T t(0) t(1) ... t(i) t(i+1)... t(i+m-2) t(i+m-1) ... t(n-1)
                 ||  ||            ||     ||
P               p(0) p(1) ...... p(m-2)  p(m-1)

为使模式P与目标T匹配，必须满足: p(0)p(1)p(2)...p(m-1) = t(i)t(i+1)t(i+2)...t(i+m-1)

朴素算法

• 以T的每个字符为起点，向后遍历，看是否与P匹配

int FintPat(string S, string P, int startIndex){
    int lastIndex = S.length() - P.length();
    if(startIndex < lastIndex){
        return (-1);
    }
    for(int g = startIndex; g<=LastIndex; g++){
        if(P == S.substr(g,P.length())){
            return g;
        }
    }
    return -1;
}

• 假定目标T的长度为n，模式P，长度为m(m<=n)
• 最坏的情况
  • 每一次循环都不成功，则一共要进行比较(n-m+1)次 – 每一次“相同匹配”比较所耗费的时间，是P和T逐个字符比较的时间，最坏情况下共m次 – 整个算法的最坏时间开销估计为O(m*n)
• 最好情况
  • 在目标的前m个位置上找到模式
    • 总比较次数：m
    • 时间复杂度：O(m)

在实际的软件开发中，大部分情况下模式串和主串都不会太长，而且匹配的时候当遇到不相等的字符时，比较就停止了，并不需要把m个字符全都看一遍。所以尽管理论意义上时间复杂度为O(n*m)，但实际上大部分情况下算法效率要比这个好的多。

KMP 算法

所谓 KMP 算法，是指在不回溯的前提下，通过某种算法来减少不必要的比较，从而最大限度的减少比较次数。在上面朴素法匹配的过程中，不难发现有很多的重复比对，比如下图所示，有目标T和模式P两个串，他们在某j个长度上匹配成功，即t(i)t(i+1)...t(i+j-1) = p(0)p(1)...p(j-1)，

T t(0) t(1) ... t(i) t(i+1) ... t(i+j-2) t(i+j-1) t(i+j)... t(n-1)
                 |   |          |        |        X
P               p(0) p(1)   ... p(j-2)   p(j-1)   p(j)

但是第j+1个位置出现了不匹配，即p(j) != t(i+j)，如果按照上面朴素算法，下一步比较应该是将p(0)向右移动一位，使其指向t(i+1)，即：

T t(0) t(1) ... t(i) t(i+1) ... t(i+j-2) t(i+j-1) t(i+j)... t(n-1)
                |    |          |        |        X
P               p(0) p(1)   ... p(j-2)   p(j-1)   p(j)
朴素匹配下一步          p(0) p(1) ... p(j-3)  p(j-2) p(j-1) p(j)

这是我们可以分析一下这一步是否有必要，假如：

1. p(0)和p(1)不相等，由于p(1)=t(i+1)，则有p(0) != t(i+1)，显然这一步匹配的结果是可以预先知道的。
2. p(0)和p(1)相等，由于p(1)=t(i+1)，则有p(0) = t(i+1)，同样，这一步匹配的结果也是可以预先知道的。

因此，无论p(0)和p(1)的关系如何，这步比较都是多余的，我们只需要通过某种方式就可以提前确定结果，因此朴素的匹配算法有是存在一定冗余的，这个冗余可以理解为，每次目标串T都需要进行回溯（已经比较到t(i+j)了，发现不等，需要回到t(i+1)的位置），因此我们该怎么移动模式串P来减少冗余的比较呢？仔细思考不难发现，这部分冗余产生的原因是因为朴素的匹配算法没有把模式串中已经比配成功的部分记录下来，这部分信息浪费掉了，导致每次都需要重新来过，我们如果可以把这部分信息以某种方式加以利用，当出现p(0) != t(i+1)时，根据这部分信息来做出移动位置的计算，使模式串P大幅度的向后滑动，则可以大大提高匹配效率。

接下来我们就研究一下，这些没有被利用的信息到底是什么。我们还是以上面这种情况作为一般情况进行分析，假设我们有下面两个串：

T |.... R   E   G   R   E   T....
        |   |   |   |   X
P |     R   E   G   R   O
                    |
P |                 R   E   G   R   O

当T和P串在E和O位置出现了不等，此时我们可以将P串直接向后移动到R的位置，为什么是R的位置，这个规律是什么呢？ 仔细观察可发现，对模式串`P`来说，如果在出现不等位置有尾串和首串相等，则可以直接将`P`向后移动到尾串的起始位置。接下来的问题就是，我们怎么知道在出现不匹配字符时，它前面的子串是否存在首尾相同的子串，以及这个子串的长度是多少呢？

这就要用到前面一节提到的字符串的next[]数组，当模式串P(j)出现失配后，检查next[j]的值，若next[j]的值不为-1或0，说明则前面子串存在相同的首尾字符串，可以将新的对其位置更新为P(j)。而 KMP 算法的核心就在于得到next[]数组，到这里我们可以大致写出 KMP 算法的雏形：

int kmp(String T, string P, int start){
    vector<int> next = buildNext(P);
    int tLen = T.length();
    int pLen = P.length();
    if(tLen - start < pLen){
        return -1;
    }
    int i=start;
    int j=0;
    while(i<tLen && j<pLen){
        if(T[i] == P[j] || j == -1){
            i++, j++;
        }else{
            j = N[j]; //注意，i不增加
        }
        if(j >= pLen){
            return i-pLen;
        }else{
            return -1;
        }
    }
}

接下来我们看一个具体例子，假设有串P和目标串T如下，其中N为模式串P的特征向量，如下：

P =  a b a b a b b
N = -1 0 0 1 2 3 4

T = a b a b a b a b a b a b a b b
    | | | | | | x
P = a b a b a b b (i=6,j=6,N[j]=4)

可以看到当比较到i=6, j=6时，T和P不相等，此时P[6]的特征向量，N[6]=4，因此下一轮需要用P[4]继续和T[6]比较，说明首串最大长度为4，相当于将P右移j-k位,即6-4=2位，得到：

T = a b a b a b a b a b a b a b b
        | | | | | | x
P =     a b a b a b b (i=8,j=6,N[j]=4)

重复上面步骤，发现在第i=8,j=6时，出现了失配，继续查表得到next[6]=4，令P[4]继续和T[8]进行比较，因此需要将P移动j-k位，即6-4=2`位

T = a b a b a b a b a b a b a b b
            | | | | | | x
P =         a b a b a b b (i=10,j=6,N[j]=4)

不断重复上述步骤，直到:

T = a b a b a b a b a b a b a b b
                    | | | | | | |
P =                 a b a b a b b

上述代码并没有特征向量next[]是怎么来的，因此接下来的问题是如何得到next[]数组，假设有子串P如下，我们先观察一下next[k]数组的一般规律。

A B Y ... A B X P(j)
    |         |

假设现在要求j位置的next[j]的值，那么，如果X和Y相同，那么next[j] = next[j-1] + 1，如果不相同则考虑X是否和P[0]相同，即X是否等于A，如果相同，则P[j]=1，不相同则P[j]=0。

接下来的问题，便是怎么用下标找出X和Y。不难看出X=P(j-1)，由于X前面的尾串AB和首串AB相同，因此可以得到next[j-1] = 2，那么可以推理得到Y=P(next[j-1])。完整算法可以实现如下：

vector<int> buildNext(string P){
    int m = P.length();
    vector<int> next(m);
    next[0] = -1;
    next[1] = 0;
    int j = 2;
    while(j < m ){
        int index = next[j-1];
        if(index != 0 && P[index] == P[j-1]){
            next[j] = next[j-1] +1;
        }else{
            if(P[j-1] == P[0] ){
                next[j] = 1;
            }else{
                next[j]=0;
            }
        }
        j++;
    }
    return next;
}

KMP 算法复杂度分析：

1. 循环体中j = N[j]; 语句的执行次数不能超过n次。否则
   • 由于j = N[]; 每一行必然使得j减少
   • 而使得j增加的操作只有j++
   • 那么，如果j = N[j];的执行次数超过n次，最终的结果必然使得j为比-1小很多的负数。这是不可能的(j有时为-1,但是很快+1回到0)。
2. 同理可以分析出求 N 数组的时间为O(m)，KMP 算法的时间为Ｏ(n+m)

LeetCode Problems

去重问题

字符串去重问题是一个很常见的问题，解法也有很多种，有些语言的库函数可以直接提供 high-level 的 API 进行去重。这里提供一个非常巧妙的解法，利用双指针+set进行一遍扫描即可。题目如下:

Given a string that contains duplicate occurrences of characters, remove these duplicate occurrences. For example, if the input string is “abbabcddbabcdeedebc”, after removing duplicates it should become “abcde”.

算法思路如下：

1. 用一个 set 保存所有不重复的字母
2. 定义两个游标，一个 read 负责读字符，一个 write 负责写字符
3. 从字符串头部开始移动 read
   • 如果 read 到集合里已经有的字符，则 read++，继续向后搜索
   • 如果 read 到 set 里没有的字符，则向 set 中添加字符，同时 write 在当前位置写入该字符, write++, read++

4. 算法伪码如下：

   read_pos = 0
   write_post = 0;
   while(read_pos < str.len){
       c = str[read_pos]
       if(c not in set){
           set.add(c)
           str[write_pos] = str[read_pos]
           write_pos += 1;
       }
       read_pos += 1
   }
   

5. 该算法的时间复杂度为O(n)，空间复杂度也为O(n)

如果我们要求不使用额外的空间，这道题该怎么解呢？显然我们需要找到另一种方式可以代替set对字符进行判重，思考前面的算法可以发现，write游标左边的字符肯定是没有重复的，因此每当read读取一个新字符时，我们都需要在[0,write)这个范围内查找一下，看看是否存在，如果存在，说明是重复字符，read继续向后搜索，write不动。如果不存在，则按照原来的逻辑write进行写入，同时更新write和read的位置。此时算法的时间复杂度变为了O(n^2)，空间复杂度为O(1)。

read_pos = 0
write_post = 0;
while(read_pos < str.len){
    c = str[read_pos]
    //修改判重方法
    if(c not in substr(0,write)){
        str[write_pos] = str[read_pos]
        write_pos += 1;
    }
    read_pos += 1
}

分割 word 问题

另一个字符串常见的问题是给定一个字符串和一个词典，判断是否可以将该字符串切割成一个或多个字典中的单词。 如下图所示

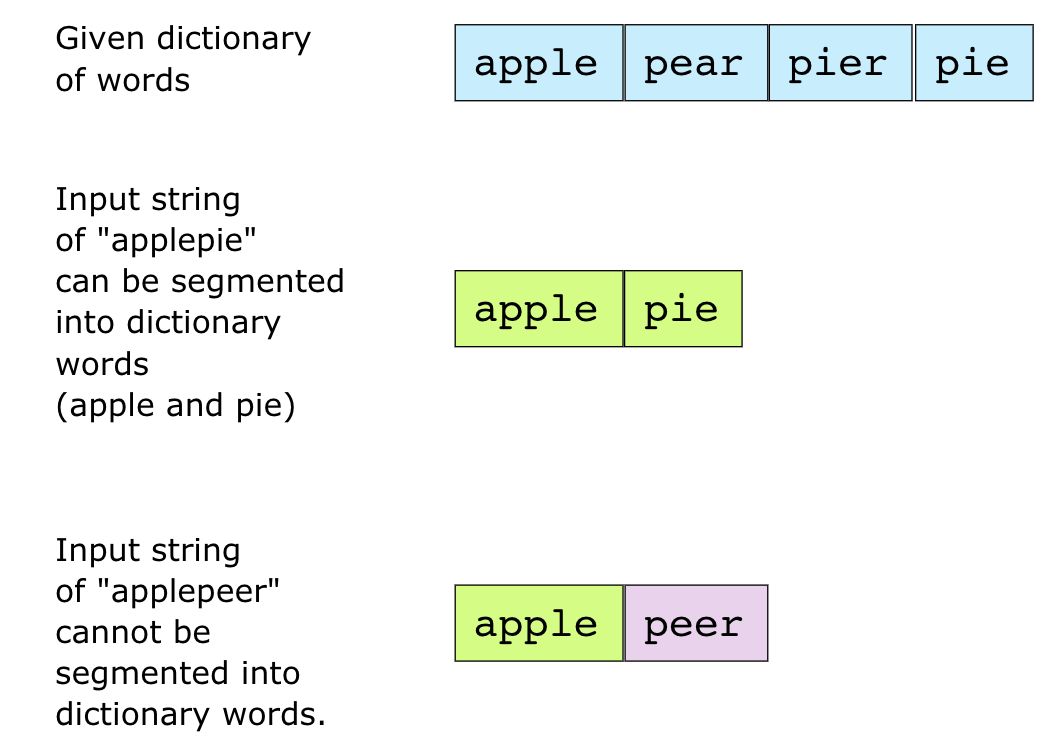
这个题的解法很多，这里使用一种记忆化递归的方式，算法思路如下：

1. 从左向右扫描字符，通过 index 分割字符为左右两部分：str1= substr(0,i),str2=substr(i+1,n-1);
2. 判断str1是否在字典中，如果不在，继续另i++向右扫描，如果在字典中，这时看str2:
   • 如果str2也在字典中，或者str2的长度为 0，则返回 true
   • 如果str2不在字典中，则对str2进行递归，重复第一步

3. 算法伪码如下

   ```
   n = length of input string
   for i = 0 to n-1
       firstword = substring (input string from index [0 , i] )
       secondword = substring (input string from index [i+1 , n-1] )
       if dictionary has firstword
           if secondword is in dictionary OR second word is of zero length, then return true
           recursively call this method with secondword as input and return true if it can be segmented
   ```
   

   我们可以模拟一个具体例子，假如输入字符串为hellonow，字典为[hello, hell, on, now]，按照上面逻辑，当 i 走到第 2 个l时，hell被分割出来如下：

hell
    onow
        on
            ow
            ow
        ono
            w
            w
        ono
hello
      now

我们可以来分析一下上述代码的时间复杂度和空间复杂度，上述过程是一个递归深搜的过程，因此时间复杂度为O(2^n)，由于每次搜索需要创建str1,str2，因此空间复杂度为O(n^2)。

上面这个例子比较简单，待分割的字符也比较短，但是极端情况我们可能会遇到分割字符非常长，且字典中的单词非常短的情况，此时会产生大量的重复计算，进而产生大量的不必要的递归导致的栈开销过高。举一个简单的例子，假如待分割的字符为aaab，字典为[a,aa]。显然，该字符是不能被正确切割的，但是计算机并不知道，我们可以分析一下可能产生的重复计算。从上面的伪码可知，递归产生于当str1满足条件后对str2的判断，因此我们只需要分析str2是否会有重复的情况即可，针对这个例子，当str1=a时，产生的str2有[aab,ab,b]会有 3 次递归，当str1=aa时，产生的str2有[ab,b]产生 2 次递归，此时我们可以看到，ab和b被重复计算了。

解决这个问题，我们需要记录曾经被计算过的，不满足条件的str2，然后在递归前先对str2进行判断，可以修改上述伪码为:

n = length of input string
for i = 0 to n-1
    firstword = substring (input string from index [0 , i] )
    secondword = substring (input string from index [i+1 , n-1] )
    if dictionary has firstword
        if secondword is in dictionary OR second word is of zero length, then return true

        if secondword in solved_set
            continue

        add secondword to solved_set
        recursively call this method with secondword as input and return true if it can be segmented

• word break
• word break II

回文串问题

检查一个字符串中是否有回文字串也是字符串常见的问题，匹配回文串的方法不难，难的是如何在字符串中找到所有的回文字串，解决这个问题有多种方法，这里介绍一种比较直观的“中心扩散法”，思路如下：

1. 从左边开始遍历字符串
2. 每访问一个字符，要考虑两种情况：
   • 中心为奇数字符情况，则以该字符为中心，向两边扩散，进行回文判定
   • 中心为偶数字符情况，则以该字符+下一个字符为中心，向两边扩散
3. 算法的时间复杂度为O(n)，空间复杂度为O(1)

我们看一个具体例子，题目要求：

Given a string, your task is to count how many palindromic substrings in this string.The substrings with different start indexes or end indexes are counted as different substrings even they consist of same characters.

Input: "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".

使用中心扩散法的代码如下

/*
 中心扩散 O(n^2)
 */
class Solution {
    int countPalindrome(int l, int r, string& s, int count){
        while(l>=0 && r < s.size()){
            if(s[l--] == s[r++]){
                count ++;
            }
        }
        return count;
    }
public:
    int countSubstrings(string s) {
        int count = 0;
        for(int i =0; i<s.length();++i){
            //中心为奇数
            count += countPalindrome(i-1,i+1,s,1);
            //中心为偶数
            count += countPalindrome(i,i+1,s,0);
        }
        return count;
    }
};

基于回文字串的问题还有很多变种，更多回文问题参考：

• 5. Longest Palindromic Substring
• 9. Palindrome Number
• 516. Longest Palindromic Subsequence

正则表达式匹配

此类问题的一般描述为，给你一个字符串，一个模式串，问该模式串是否可以匹配给定的字符串。通常在模式串中，存在某些通配符，例如.和*。假设给定字符串s="fabbbc"，给定的模式串p=".ab*c"。我们从第一个字符开始匹配，由于.可以匹配任何字符，因此第一个字符 match，接下来我们需要继续比较s=abbbc和p=ab*c，显然s[0]和p[0]匹配，接下来我们继续匹配s=bbbc和p=b*c。可以看出上述匹配过程是一个递归的过程，每当我们完成一次匹配后，用剩余的字符继续匹配。

接下来我们可以总结一下匹配规则：

1. 当s和p的长度都为 0 时，说明匹配完成，此时返回 true
2. 当s和p的长度都为 1 时，判断p[0] = '.' || p[0] == s[0]

3. 当p的长度大于 1 时，check p[1]=='*'

   • 如果p[1] != '*'，判断p[0] = '.' || p[0] == s[0]，如果 match，则递归比较p.substr(1)和s.substr(1)。如果不 match 则返回 false
   • 如果p[1] == '*'，此时情况比较复杂，我们可以枚举一些情况
     1. s="", p="b*"
     2. s="a", p="b*"
     3. s="a", p="b*a"
     4. s="bb", p="b*"
     5. s="bba", p="b*a"
     6. s="a", p="a*a"

   上面的前三种情况可以归结为一种情况，即比较p.substr(2)和s，由于*代表 0 个或者多个，如果将b*从p中去掉仍然可以匹配，那么s和p就是匹配的。而对于后面两种情况，我们则不能简单的将b*去掉，比如在第 4 个例子中，如果去掉b*，则s="bb"和p=""，显然是不匹配的，而实际上s="bb"是满足p="b*"的。因此这种情况下，我们需要不断的改变 s，以第 5 个例子为例，当发现s[0] == p[0] || p[0]=='.'后，令s=s.substr(1)继续比较，直到s="a",p="b*a"，此时再进行一次递归即可回到上面前三条的逻辑。但是这里我们又遗漏了一个场景，即上面第 6 条，按照之前的逻辑，我们最终会走到s="",p="a"的判断，显然结果是不正确的。出现这个问题的原因在于，我们不知道b*后面是否还有其它字符，因此正确的做法是，没当更新一次 s 时，都需要先进行一次递归比较。

4. 综上，上述三条规则可以涵盖所有的场景

bool isMatch(string s, string p){
    if(s.empty() &&  p.empty()){
        return true;
    }
    if( p.size() ==1){
        return s.size()==1 && s[0]==p[0] || p[0]=='.';
    }
    if ( p[1] != '*' ){
        if(s.empty()){
            return false;
        }
        if (s[0]==p[0] || p[0]=='.'){
            return isMatch(s.substr(1),p.substr(1));
        }else{
            return false;
        }
    }

    //p[1] == '*'
    //s="bba", p="b*a"
    while(!s.empty() && (s[0] == p[0] || p[0]=='.'){
        if(isMatch(s,p.substr(2)){
            return true;
        }
        //update s
        s = s.substr(1);
    }
    /*
        s="a", p="b*a"
        s="x", p="b*"
    */
    return isMatch(s,p.substr(2));
}

• 10. Regular Expression Matching
• 44. Wildcard Matching

滑动窗口问题

滑动窗口是用来寻找符合某种条件子串的一种线性扫描方法，它通过记录滑动窗中字符个数的变化来判断当前状态是否满足条件。其模板如下

//str is input
//p is pattern
T slidingWindow(string str, string p){
    //1. create a hashmap, key is char, value is count
    unordered_map<char, int> um;
    for(auto &c : p){
        um[c]++;
    }
    int counter = um.size();

    //2. create a sliding window
    int left =0; int right = 0;
    int len = INT_MAX;

    //3. expand right boundary
    while(right < str.length()){
        char c = str[right];
        //check if c is in the um
        if(um.count(c) > 0){
            um[c]--;
            //todo: check point #1
            if(um[c]==0){
                counter -=1;
            }
        }

        //todo: check point #2
        //check if counter is zero
        while(counter == 0){
            //todo: check point #3
            //calculate len,
            int length = right -left +1;

            //move left boundary
            char c = str[left];
            if(um.count(c) > 0){
                um[c]++;
                if(um[c] > 0){
                    counter++;
                }
            }
            //expand the left boundary
            left ++;
        }
        //expand the right boundary
        right ++;
    }
    //todo:
    return some_thing;
}

• 3. Longest Substring Without Repeating Characters
• 76. Minimum Window Substring
• 438. Find All Anagrams In a String

Resources

• Pattern Matching Pointer
• 字符串匹配算法的描述、复杂度分析和 C 源代码
• CS106B-Stanford-YouTube
• Algorithms-Stanford-Cousera
• 算法与数据结构-1-北大-Cousera
• 算法与数据结构-2-北大-Cousera
• 算法与数据结构-1-清华-EDX
• 算法与数据结构-2-清华-EDX
• 算法设计与分析-1-北大-Cousera
• 算法设计与分析-2-北大-EDX