二叉树

Posted on 2008-07-20 | In DataStructure

基本概念

二叉树 (binary tree)由节点的有限集合构成
- 这个有限集合或者为空集 (empty)
- 或者为由一个根节点 (root) 及两棵互不相交、分别称作这个根的左子树(left subtree)和右子树 (right subtree) 的二叉树组成的集合

节点
- 子节点、父节点、最左子节点
- 兄弟节点、左兄弟、右兄弟
- 分支节点、叶节点
  - 没有子树的节点称作叶节点（或树叶、终端节点）
  - 非终端节点称为分支节点
边
- 两个节点的有序对，称作边
- 路径，路径长度
- 祖先，后代
  - 若有一条由k到达k(s)的路径，则称k是k(s)的祖先，k(s)是k的子孙
层数
- 根为第 0 层,其他节点的层数等于其父节点的层数加 1
- 深度：层数最大的叶节点的层数
- 高度：层数最大的叶节点的层数加 1
满二叉树和完全二叉树
- 满二叉树
  - 所有非叶子节点的节点度为2
- 完全二叉树
  - 若设二叉树的深度为h，除第h层外，其它各层是满的
  - 第h层如果不是满的，则子节点都在最左边
扩充二叉树
- 所有叶子节点变成内部节点，增加树叶，变成满二叉树
- 所有扩充出来的节点都是叶子节点
- 外部路径长度E和内部路径长度I满足：E=I+2n(n是内部节点个数)

二叉树性质

在二叉树中，第i层上最多有 $2i (i≥0)$ 个节点
深度为 k 的二叉树至多有 $2^{(k+1)}-1 (k≥0)$ 个节点
- 其中深度(depth)定义为二叉树中层数最大的叶节点的层数
一棵二叉树，若其终端节点数为$n_0$，度为$2$的节点数为$n_2$，则 $n_0=n_2+1$
满二叉树定理：非空满二叉树树叶数目等于其分支节点数加1
满二叉树定理推论：一个非空二叉树的空子树数目等于其节点数加1
有$n$个节点$(n>0)$的完全二叉树的高度为$⌈\log_2(n+1)⌉$，深度为$⌈\log_2(n+1)- 1⌉$

二叉树的存储结构

二叉树的各节点随机地存储在内存空间中，节点之间的逻辑关系用指针来链接。我们可以使用二叉链表的方式来表示一个节点，其中left,right两个指针指向左右两个子树，info表示该节点的值，如下：

template<class T>
class BinaryTreeNode{
    BinaryTreeNode<T> *left; // 指向左子树的指针
    BinaryTreeNode<T> *right; // 指向右子树的指针
    T info;
};

对于某些场景，我们也可以在上述结构中再增加一个指向父节点的parent指针，使其变为三叉链表：

template<class T>
class BinaryTreeNode{
    BinaryTreeNode<T> *left; // 指向左子树的指针
    BinaryTreeNode<T> *right; // 指向右子树的指针
    BinaryTreeNode<T> *parent; // 指向父节点的指针
    T info;
};

接下来我们来分析一下使用二叉链表的空间开销，我们令存储密度$\alpha$表示数据结构存储的效率，结构性开销 $\gamma=1-\alpha$，则有

$\alpha=\frac{数据本身存储量}{整个结构占用的存储总量}$

满二叉树为例，满二叉树的一半指针域为空，每个节点存在两个指针，一个数据域，则需要的总空间为(2p+d)*n，如果p=d，那么结构性开销为2p/(sp+d)=2/3，可见满二叉树存储效率并不高，有三分之二的结构性开销。

完全二叉树的顺序存储

由于完全二叉树的结构，可以将二叉树节点按一定的顺序存储到一片连续的存储单元，使节点在序列中的位置反映出相应的结构信息
- 存储结构实现性的
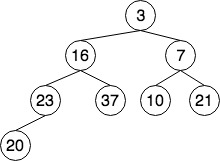
  - 如下图的完全二叉树，其存储结构为|3|16|7|23|37|10|21|20|
  - 我们可以根据一维数组的下标来定位节点的位置
- 逻辑结构上仍然是二叉树结构

下标公式
- 当2i+1<n时，节点i的左孩子是节点2i+1，否则节点i没有左孩子
- 当2i+2<n 时，节点i的右孩子是节点2i+2，否则节点i没有右孩子
- 当0<i<n 时，节点i的父亲是节点⌊(i-1)/2⌋
- 当i为偶数且0<i<n时，节点i的左兄弟是节点i-1，否则节点i没有左兄弟
- 当i为奇数且i+1<n时，节点i的右兄弟是节点i+1，否则节点i没有右兄弟

二叉树的遍历

遍历是一种将树形结构专户为线性结构的方法，对二叉树来说，有4种遍历的次序，分别是

前序法 (tLR次序，preorder traversal)。
- 根节点->左子树->右子树。
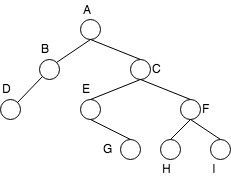
- 上图：ABDCEGFHI
中序法 (LtR次序，inorder traversal)。
- 左子数->根节点->右子树。
- 上图：DBAEGCHFI
后序法 (LRt次序，postorder traversal)。
- 左子树->右子树->根节点
- 上图：DBGEHIFCA
层次遍历
- 按节点所在层，从上到下依次遍历
- 上图：ABCDEFGHI

从图论的角度讲，前三种遍历方式也叫做深度优先遍历，最后一种叫做广度优先遍历。

深度优先遍历

由于二叉树的前中后遍历次序具有自相似性，因此可以很方便的使用递归的方式实现

//递归，前序遍历
template<class T>
void traverse (BinaryTreeNode<T>* root){
    if(!root){
        return ;
    }
    //Visit(root); //前序遍历
    traverse(root->left); // 递归访问左子树
    //Visit(root); // 中序
    traverse(root->right); // 递归访问右子树
    //Visit(root); // 后序
｝

递归遍历的时间复杂度为 $T(n)=O(1) + T(a) + T(n-a-1) = O(n)$ 这是一个不能再好的时间复杂度了。

迭代实现

上面介绍的递归遍历是一种简洁并很好理解的算法，而且编译器也会在递归过程中做一些优化，因此效率并不会太差，但是对树层次很深的情况下，可能会有栈溢出的隐患，此时可以将递归解法转为非递归的迭代解法。

前序遍历

template<class T>
void BinaryTree<T>::None_Recursive_1(BinaryTreeNode<T>* root){
    stack<BinaryTreeNode<T>* > ss;
    BinaryTreeNode<T>* pointer = root;
    ss.push(NULL);// 栈底监视哨
    while(pointer){
        Visit(pointer->value()); //遍历节点
        if(pointer->right){
            ss.push(pointer->right); //如果该节点有右子树，入栈
        }
        if(pointer->left){ //循环遍历左子树
            pointer = pointer->left;
        }else{
            pointer = ss.top(); //右子树
            ss.pop();
        }
    }
}

也可以通过判断栈是否为空作为循环条件，思路为：

将根节点放入栈中
判断栈是否为空，如果不空，取出栈顶节点访问
如果该节点有右子树，入栈右子树
如果该节点有左子树，入栈左子树
重复第2步

template<class T>
void BinaryTree<T>::None_Recursive_2(BinaryTreeNode<T>* root){
    stack<BinaryTreeNode<T>* > ss;
    ss.push(node);
    while(!ss.empty()){
        BinaryTreeNode<T>* top = ss.top();
        Visit(top);
        ss.pop();
        if(top->right){
            ss.push(top->right); //先入栈右子树节点
        }
        if(top->left){ 
            ss.push(top->left); //后入栈左子树节点
        }
    }
}

中序遍历

指针指向根节点
遇到一个节点，入栈一个节点，指针指向左子节点，继续下降
左节点为空时，弹出一个节点，指针指向该节点
指针指向右节点
循环第1步

void inOrder_Traverse(TreeNode* root){
    stack<TreeNode* >st;
    TreeNode* pointer = root;
    while(!st.empty() || pointer){
        if(pointer){
            st.push(pointer);
            pointer = pointer->left;
        }else{
            pointer = st.top();
            st.pop();
            Visit(pointer);
            pointer = pointer -> right;
        }
    }
}

后序遍历

后序遍历相对复杂，需要给栈中元素加上一个特征位：

Left 表示已进入该节点的左子树，将从左边回来
Right 表示已进入该节点的右子树，将从右边回来

enum Tag{left, rigt};
class TreeNodeElement{
    TreeNode* node;
    Tag tag;
    TreeNodeElement(TreeNode* n):node(n){
        tag = left;
    }
};

遍历的具体步骤为：

指针指向根节点
如果当前指针不为空，指针沿着左子节点下降，将途径节点标记为left，并入栈
左节点下降到末尾后，将栈顶元素弹出
如果该元素来自left，将其将其标记为right，重新入栈，指针指向右节点，并沿右节点下降
如果该元素来自right，访问该节点，并将指针置为空 6，重复第2步

void postOrder_Traversal(TreeNode* root){
    stack<TreeNodeElement> st;
    TreeNode* pointer =  root;   
    while(pointer || !st.empty()){
        while(pointer){
            TreeNodeElement ele(pointer); // 沿非空指针压栈，并左路下降
            ele.tag = left;
            st.push(ele); // 把标志位为Left的节点压入栈
            pointer = pointer->left;
        }
        //左子节点下降完毕
        TreeNodeElement ele = st.top();
        st.pop();
        pointer = ele.pointer;
        if(ele.tag == left){ //来自左边
            //将其更改为右边，重新入栈
            ele.tag = right;
            st.push(tag);
        }else{
            //visit节点
            visit(pointer);
            pointer = NULL; //置为NULL，继续弹栈
        }
    }
}

实际上对于后序遍历的迭代实现还有更为巧妙的一种方法，这种方法的思路和前序遍历类似，前序遍历的顺序为：根–>左节点–>右结点，我们稍微修改一下这个顺序，将其改为：根–>右结点–>左节点。我们按照这个顺序来遍历二叉树会得到一组结果，接下来我们只需要将该结果reverse一下即可得到后序遍历的结果。我们看一个例子

上面这棵二叉树按照上面提到的遍历次序，得到结果为4 3 2 1，将该序列翻转后得到1 2 3 4，即后序遍历结果。我们可以先用递归形式的代码模拟这个过程：

void traverse (TreeNode* root){
    if(!root){
        return ;
    }
    Visit(root); 
    traverse(root->right); //先访问右结点
    traverse(root->left;
｝

将上述代码转为迭代的形式为：

 vector<int> postOrder_Traversal(TreeNode* root) {
        if(!root){
            return {};
        }
        vector<int> res;
        stack<TreeNode* > stk;
        stk.push(root);
        while(!stk.empty()){
            TreeNode* node = stk.top();
            stk.pop();
            res.push_back(node->val);
            if(node->left){
                stk.push(node->left);
            }
            //先访问右子树，后入栈
            if(node->right){
                stk.push(node->right);
            }
        }
        //结果reverse
        return {res.rbegin(),res.rend()};
    }

这种方式的迭代实现比起第一个版本要容易很多，实际应用中也更容易编写，不易出错。

复杂度分析

时间复杂度
- 在各种遍历中，每个节点都被访问且只被访问一次，时间代价为`O(n)`
- 非递归保存入出栈（或队列）时间
  - 前序、中序，某些节点入/出栈一次，不超过O(n)
  - 后序，每个节点分别从左、右边各入/出一次， O(n)
空间复杂度
- 栈的深度与树的高度有关
  - 最好 O(log n)
  - 最坏 O(n) ，此时树退化为线性链表

广度优先遍历

从二叉树的第0层（根节点）开始，自上至下逐层遍历；在同一层中，按照从左到右的顺序对节点逐一访问。例如上图中，广度优先遍历的顺序为:ABCDEFGHI

template<class T>
void BinaryTree<T>::LevelOrder (BinaryTreeNode<T>* root){
    queue<BinaryTreeNode<T>*> qq; //广搜使用队列
    BinaryTreeNode<T>* pointer = root;
    qq.push(pointer);
    while(!qq.empty()){
        pointer = qq.front();
        qq.pop();
        Visit(pointer->value());
        if(pointer->leftchild()){ //左子树入队
            qq.push(pointer->leftchild());
        }
        if(pointer->rightchild()){
            qq.push(pointer->rightchild()); //右子树入队
        }
    }
}

时间复杂度
- 在各种遍历中，每个节点都被访问且只被访问一次，时间代价为O(n)
- 非递归保存入出栈（或队列）时间
  - 宽搜，正好每个节点入/出队一次，O(n)
空间复杂度
- 与树的最大宽度有关
  - 最好 O(1)
  - 最坏 O(n)

二叉树