堆
堆是完全二叉树的一种表现形式。以最小堆为例,它要求的每个父节点的值大于两个子节点的值,两个兄弟节点之间的值的大小关系没有限制。由于完全二叉树可以用数组表示,上述性质也可以表述为:
- $K_1<=K_{2i+1}$
- $K_1<=K_{2i+2}$
因此使用最小堆可以找出这组节点的最小值。推而广之,对于一组无序的数,可以将他们构建成堆来快速得到最大值或最小值,当有新元素进来时,堆也依然可以保持这种特性
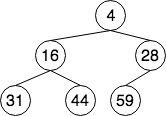
堆的核心操作有如下三种
- 建堆,将一组无序的数组织成堆的形式
- 思路1:将n数组成的无序数组进行原地建堆操作
- 思路2:将n个无序的数一个一个进行插入操作
- 新元素入堆后如何调整堆
- 将其放到数组最右边的位置
- 递归进行
SiftUp调整
- 堆顶元素出堆后如何调整
- 将数组最后一个节点的值付给堆顶元素
- 删除最后一个元素
- 堆顶节点递归进行
SiftDown调整
堆的表示
正如前文所述,由于堆是一种完全二叉树,我们可以用数组表示,如上图中的小顶堆可用数组[4,16,28,31,44,59]表示。对于数组中的任意元素,下标为i的节点的左孩子节点的下标为i*2+1,右孩子节点的下标为2*i+2,父节点的坐标为(i-1)/2。
class Heap{
vector<int> heap;
int n; //堆大小
int count; //堆中元素个数
public:
Heap(int capicity){
heap = vector<int>(capacity, 0);
n = capacity;
count = 0;
}
Heap(vector<int>& arr){
capacity = arr.size();
count = capacity;
heap = arr;
buildHeap(heap);
}
void buildHeap(vector<int>& arr);
void push(int data);
int top(){ return heap[0]; };
void pop();
private:
int left_child_index(int pos){
int index = pos*2+1;
return index >= n?-1:index;
}
int right_child_index(int pos){
int index = pos*2+2;
return index?=n?-1:index;
}
int parent_index(int pos){
return (pos-1)/2;
}
void sift_up(size_t pos);
void sift_down(size_t pos);
};
SiftDown调整
所谓SiftDown调整,即将一个不合适的父节点下降到合适的位置。以小顶堆为例,我们需要考虑四种情况:
//递归调整
void sift_down(vector<int>& heap, size_t position){
//找到左右节点的index
size_t l = left_child_index(position);
size_t r = right_child_index(position);
//待删除节点为叶子节点
if(l == -1 && r == -1){
return;
}
//待删除节点左子节点为空,说明当前已经是叶子节点
else if(l == -1 ){
return;
}
//待删除节点的右子节点为空,比较左节点
else if(r == -1 ){
if(heap[i] > heap[l]){
swap(heap[i], heap[l]);
sift_down(l);
}
}else{
//待删除节点的左右子节点都不空,找到最小的
size_t index = heap[l] < heap[r] ? l:r;
if(heap[i] > heap[index]){
swap(heap[i],heap[index]);
sift_down(index);
}
}
}
SiftUp调整
和SiftDown类似,SiftUp调整是将一个不合适的子节点上升到合适的位置,例如新元素进入堆之后,该元素要进行SiftUp调整
void sift_up(vector<int>& heap, size_t pos){
if(pos == 0){
return;
}
int p = parent_index(pos);
if(heap[pos]<heap[p]){
//交换父子节点
swap(heap[pos], [p]);
//递归调整
sift_up(p);
}
}
建堆
了解了堆调整的两个算法后,我们可以用上面的方法来建堆。如上文所述,建堆有两种思路,其中第二种思路较为简单,可以退化为入堆操作,第一种思路需要按下面步骤操作:
- 将
n个关键码放到一维数组中,整体不是最小堆 - 由完全二叉树的特性,有一半的节点
⌊n/2⌋是叶子节点,它们不参与建堆的过程i≥⌊n/2⌋时,以关键码Ki为根的子树已经是堆
- 从倒数第二层最右边的非叶子节点开始(完全二叉树数组
i=⌊n/2-1⌋的元素),依次向前,进行递归SiftDown调整。
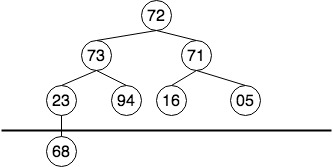
例如上图中,我们有一组8个数的无序序列{72,73,71,23,94,16,05,68},建堆步骤为
- 按照完全二叉树排布,形成树形结构,如上图
- 成树后,可以看到有4个节点(
⌊4/2⌋)已经是叶子节点,它们不需要参与建堆的过程 - 从
23开始(数组第i=⌊4/2-1⌋=3项)依次进行sift_down调整,顺序依次是:23,71,73,72
void buildHeap(vector<int>& heap){
for (int i=count/2-1; i>=0; i--)
sift_down(heap,i);
}
}
分析一下建堆的效率:
- $n$个节点的堆,高度为$d=⌊\log_2^{n}+1⌋$,设根为第$0$层,第$i$层节点数为$2^i$
- 考虑一个元素在队中向下移动的距离
- 大约一半的节点深度为$d-1$,不移动(叶)。
- 四分之一的节点深度为$d-2$,而它们至多能向下移动一层。
- 树中每向上一层,节点的数目为前一层的一半,而子树高度加一。
- 因此元素移动的最大距离的总数为:
插入元素
对于插入操作,我们首先将待插入元素放到数组末尾,然后利用前面提到的sift_up算法,让新插入的节点与父节点对比大小,如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。一直重复这个过程,直到父子节点之间满足刚说的那种大小关系。
void push(vector<>int data){
if(count >= n){
return ; //堆满了
}
++count;
heap[count] = data;
//递归调整
sift_up(heap,count);
}
删除元素
对于堆来说,由于不支持随机访问,删除元素指的就是删除堆顶元素。以小顶堆为例,当我们删除堆顶元素之后,就需要把第二小的元素放到堆顶,而第二小元素肯定会出现在左右子节点中,于是我们可以将堆顶元素和第二小的个元素进行交换,然后我们再递归删除交换后的这个节点,以此类推,直到叶子节点被删除。
而实的删除算法并不会按照上面思路执行,而是会用到一个小技巧,即我们先将数组中最后一个元素的值和堆顶互换,然后删除数组中最后一个元素(即删除了堆顶元素)。接下来,对于新的堆顶元素,进行上面提到的sift_down操作,直到找到合适位置。
void pop(){
if(count == 0){
return ; //堆中没有数据
}
heap[0] = heap[count]; //交换堆顶和末尾元素
heap.pop_back(); //删除末尾元素
--count ;
//堆顶元素sift_down
sift_down(heap,1);
}
堆操作时间复杂度分析
建堆的效率前面已经分析过了为O(n),对于插入和删除操作来说,它们的主要操作是sift_down和sift_up操作,这两种操作每次均是向上或者向下跨越一层,因此时间复杂度和树的高度成正比,也就是O(logn)。
堆的其它实现
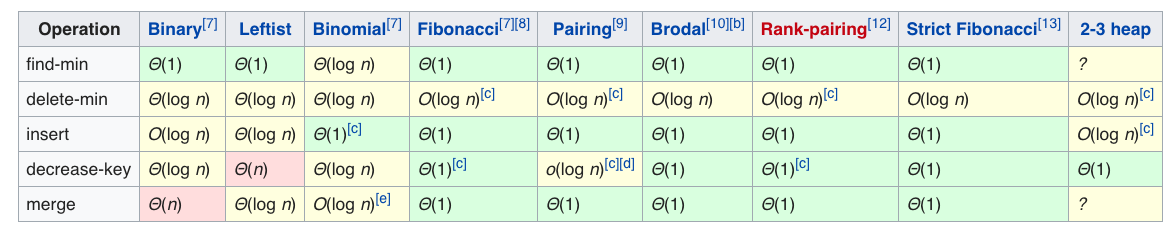
上面介绍的建堆的方式是最基本的二叉堆(Binary Heap),除了这种方式以外还有很多种其它建堆的方式,比如使用BST,红黑树等。不同的建堆方式其性能也不尽相同,这里附上一张对比图
堆排序
我们可以利用堆顶每次返回最优解这个特性来对数组进行原地排序,也就是所谓的堆排序。假设我们要从小到大排序,这时候我们需要建一个大顶堆,按照大顶堆的特性,堆顶元素为数组最大元素,我们把它跟最后一个元素交换,那最大元素就放到了下标为n的位置。接下来为了保持堆的特性,我们需要对新的堆顶进行sift down操作,这样剩下的n-1个元素又构成了新的大顶堆。我们再取堆顶的元素放到n-1的位置,重复这个过程,直到堆中只剩一个元素,排序工作就完成了。
void heap_sort(vector<int>& a){
buildHeap(a);
int k = a.size()-1;
while(k>=0){
swap(a[0],a[k]);
--k;
sift_down(a,0);
}
}
上面的堆排序算法包含两个过程,建堆过程和堆调整过程,总的时间复杂度为O(n) + O(n*log(n)) = O(nlog(n))。由于存在元素交换,因此堆排序不是稳定排序。
堆的相关应用
- 求一个无序数组中第K大的元素
这是一道经典的面试题,如果不熟悉堆这种数据结构,首先想到的应该是排序。将数组排序后,从头开始向后遍历k个元素,得到最终结果。这种方式当数组较大的时候,效率并不高,时间复杂度为O(Nlog(N)) + O(K),不是一种线性解法。
另一种思路是,当K值较小的情况,比如k=3,此时可以采用遍历k次数组的方式,第一次找到最大值,第二次找到次大值,依次类推…,这种方式的时间复杂度为K*O(N)比前面方法要好一些
这道题比较经典的方法是使用堆来解,扫描一遍数组即可。其思路为,建立一个k大小最小堆,如果数组中的元素比堆顶的大,则pop掉堆顶元素,入堆新元素。依次类推,最后堆中存放的是数组中前k个最大值元素,返回推顶元素即可。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int,std::vector<int>,std::greater<int>> pq;
for(auto x:nums){
if(pq.size()<k){
pq.push(x);
}else{
if(x>pq.top()){
pq.pop();
pq.push(x);
}
}
}
return pq.top();
}
};
上述算法,遍历数组需要O(n)时间复杂度,一次push或pop操作需要 O(logK) 的时间复杂度,所以最坏情况下,n个元素都入堆一次,所以时间复杂度就是O(nlogK)。
- 无序数组中位数问题
这也是一道经典的面试题,常规做法还是对数组排序,然后选出中位数。显然这种方式的时间复杂度和上面的例子相同,为O(Nlog(N) + O(N/2))。
如果使用堆,我们则无需排序即可找出中位数,如果做到呢?首先,我们需要维护两个堆,一个堆是小顶堆和一个堆是大顶堆,大顶堆中存储前半部分数据,小顶堆中存储后半部分数据,且小顶堆中的数据都大于大顶堆中的数据。如果数组的大小为偶数,则大小堆的size均为n/2,中位数为大小堆堆元素中的某一个。如果数组的大小为奇数,则可以令大顶堆的size为n/2+1,则中位数为大顶堆的堆顶元素。
int findMedium(vector<int>& arr){
priority_queue<int> maxHeap;
priority_queue<int,std::vector<int>,std::greater<int>> minHeap;
for(auto x : arr){
if(maxHeap.empty() || x < maxHeap.top()){
maxHeap.push(x);
}else{
minHeap.push(x);
}
//adjust size
if(minHeap.size() > maxHeap.size()){
maxHeap.push(minHeap.top());
minHeap.pop();
}
if(maxHeap.size() - minHeap.size() > 1){
minHeap.push(maxHeap.top());
maxHeap.pop();
}
}
return maxHeap.top();
}
