霍夫曼树

Posted on 2008-08-04 | In DataStructure

霍夫曼(Huffman)树

霍夫曼树是一种特殊的二叉树组织形式，用来实现霍夫曼编码，霍夫曼编码是一种不等长编码技术。所谓非等长编码，是根据字符出现的频率高低对字符进行不同位数的编码，一般希望经常出现的字符编码比较短，不经常出现的字符编码较长。

Z  K  F  C  U  D  L  E
2  7  24 32 37 42 42 120

例如上面字符中，每个下面为其对应出现的频率。我们可以对这些字符进行编码，例如Z=111100，K(111101)。每个字符的编码需要满足一个条件，即编码规则为前缀编码。所谓前缀编码要求任何一个字符的编码都不是另外一个字符编码的前缀，这种前缀特性保证了译码的唯一性。

Z(111100),K(111101),
F(11111),C(1110),
U(100),D(101), 
L(110),E(0)

假设我们已经有了上述的编码表，对于000110可以翻译出唯一的字符串EEEL。因此我们需要寻找一种编码方法使得：

频率高的字符占用存储空间少
编码规则符合前缀码要求

将这个问题抽象一下，对于$n$个字符$K_0$，$K_1$，…，$K_{n-1}$，它们的使用频率分别为$w_0$, $w_1$，…，$w_{n-1}$，给出它们的前缀编码，使得总编码效率最高

霍夫曼树

为了实现上述编码规则，我们需要设计这样一棵树：

给出一个具有$n$个外部节点($n$个待编码字符)的扩充二叉树
令该二叉树每个外部节点$K_i$ 有一个权 $w_i$ 外部路径长度为$l_i$
使这个扩充二叉树的叶节点带权外部路径长度总和为$\sum_{i=0}^{n-1}l_i * w_i $ 最小

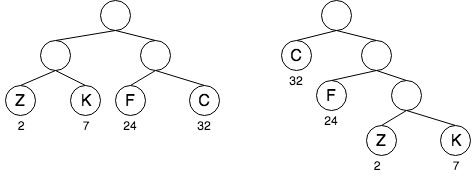
我们把具有这样性质的树叫做Huffman树，它是一种带权路径长度最短的二叉树，也称为最优二叉树。如下图中，左边树构建方式的带权路径和为：(2+7+24+32)x2 = 130, 右边树构建方式的带权路径和为：32x1+24x2 +(2+7)x3 = 107。

构建Huffman树

贪心法

将节点按照权值从小到大排列
拿走前两个权值最小的节点，创建一个节点，权值为两个节点权值之和，将两个节点挂在新节点上
将新节点的权值放回序列，使权值顺序保持
重复上述步骤，直到序列处理完毕 5，所有待编码的节点都处在叶子位置

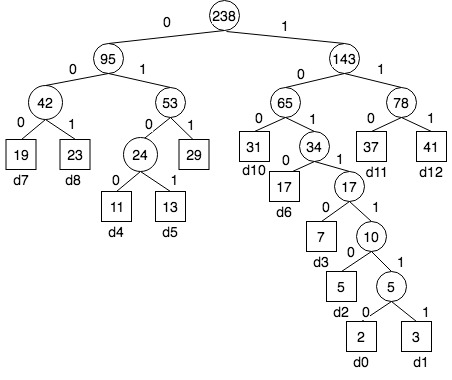
假设有一组节点的优先级序列为: 2 3 5 7 11 13 17 19 23 29 31 37 41，对应的Huffman树为：

编码

有了Huffman树，就可按路径对叶子节点(待编码字符)进行霍夫曼编码，例如上图中的每个叶子节点的编码为：

d0 ： 1011110   d1 ： 1011111
d2 ： 101110    d3 ： 10110
d4 ： 0100      d5 ： 0101
d6 ： 1010      d7 ： 000
d8 ： 001       d9 ： 011
d10： 100       d11 ：110  d12： 111

//前序遍历，得到每个叶子节点的霍夫曼编码
void traverse(HuffmanTreeNode* root, vector<int>& codes){
    
    if(root&&root->left==NULL&&root->right==NULL){
        for(auto num : codes){
            cout<<num<<" ";
        }
        cout<<endl;
    }
    
    if(root->left){
        codes.push_back('0');
        traverse(root->left,codes,dictionary);
        codes.pop_back(); //回溯
    }
    
    if(root->right){
        codes.push_back('1');
        traverse(root->right, codes,dictionary);
        codes.pop_back();//回溯
    }
};

译码

与编码过程相逆，从左至右逐位判别代码串，直至确定一个字符

从树的根节点开始
- 0下降到左分支
- 1下降到右分支
到达一个树叶节点，对应的字符就是文本信息的字符
译出了一个字符，再回到树根，从二进制位串中的下一位开始继续译码

译码: 111101110

111 -> d12
101110 -> d0

111101110 ->d12d0

构建Huffman树

HuffmanTree(vector<int> weight, TreeNode* root;){
    HuffmanTreeNode* root; 
    HuffmanTree(vector<int>& weight){
        priority_queue<HuffmanTreeNode*,std::vector<HuffmanTreeNode* >,comp> heap; //最小堆
        size_t n = weight.size();
        for(int i=0; i<n; ++i){
            HuffmanTreeNode* node = new HuffmanTreeNode();
            node->weight = weight[i];
            node->left = node->right = node->parent = NULL;
            heap.push(node);
        }
        for(int i=0; i<n-1; i++){ //两个节点合成一个，共有n-1次合并建立Huffman树
            HuffmanTreeNode* first = heap.top();
            heap.pop();
            HuffmanTreeNode* second = heap.top();
            heap.pop();
            HuffmanTreeNode* parent = new HuffmanTreeNode();
            first->parent = parent;
            second->parent = parent;
            parent->weight = first->weight + second->weight;
            parent->left  = first;
            parent->right = second;
            heap.push(parent);
            root = parent;
        }
}

编码效率

设平均每个字符的代码长度等于每个代码的长度$c_i$, 乘以其出现的概率$p_i$ ，即:

\[l = c_0p_0 + c_1p_1 + … + c_{n-1}p_{n-1}\]

其中$p_i=f_i / f_T$, $f_i$为第$i$个字符的出现的次数，而$f_T$为所有字符出现的总次数。因此前面式子也可以写为

\[c_0f_0 + c_1f_1 + … + c_{n-1}f_{n-1}) / f_T\]

则上图中的平均码长度为

\[(3*(19+23+24+29+31+34+37+41)+4*(11+13+17)+ 5 * 7+6 * 5+7*(2+3)) / 238 = 804 / 238 ≈ 3.38\]

对于这13个字符，如果采用等长编码每个字符需要$⌈log13⌉=4$位，显然Huffman编码效率更高，只需要等长编码$3.38/4≈ 84\% $ 的空间

应用
- Huffman编码适合于字符频率不等，差别较大的情况
- 数据通信的二进制编码
  - 不同的频率分布，会有不同的压缩比率
  - 大多数的商业压缩程序都是采用几种编码方式以应付各种类型的文件
    - Zip 压缩就是 LZ77 与 Huffman 结合
- 归并法外排序，合并顺串

霍夫曼树

霍夫曼(Huffman)树

Resources