并查集与Trie
并查集
并查集是一种特殊的集合,由一些不相交子集构成。它有两个基本操作是:
- Find(x): 确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集
- Union(x,y): 归并两个集合
并查集是重要的抽象数据类型,用于求解等价类等等问题,所谓等价类是指:相互等价的元素所组成的最大集合。例如,我们有一系列整数对<1,2> <5,1> <1,6> <0,3> <7,4> <6,9> <5,3> <0,8> <4,8>,每个整数对表示一组等价关系(等价对),以第一组<1,2>为例,我们假设等价关系为”元素1和元素2是相互连通的”。那么我们希望能通过某种算法,去掉上面某些无意义的等价对,从而得到若干个集合,集合中的每个元素都是彼此连通的。比如,在处理一个整数对<p,q>时,判断它们是否处于同一个集合,如果是,则忽略它们(无意义的等价对);如果不是,我们需要将$p$所属的集合和$q$所属的集合进行归并(union操作),最终所有整数处于同一个或者若干个大的集合中。
我们可以使用树来表示一个集合(用父节点代替),每个节点的子节点为该集合的子集,如果两个节点处于同一棵树中,那么这两个节点代表的两个子集处于同一个集合。
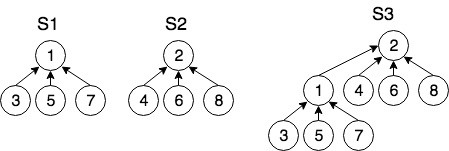
如上图所示,有两个等价类集合$S_1,S_2$。在$S_1$中,有<3,1>,<5,1>,<1,7> 三个等价对,由等价关系可知3,5,7彼此等价,并且它们具有相同的根节点1;$S_2$的情况通力同理,假如现在引入另一个等价对<3,2>,可以发现,3的根节点为2,不等于1,因此如果要建立等价关系,需要将$S_1,S_2$合并,这样两个集合中的元素都将有相同的根节点。
并查集的实现
为了实现上面的并查集,可采用前面一节提到的父节点表示法(数组)作为树的存储结构,数组的索引为每个节点的值,数组的元素为该节点的父节点,这样每个节点可以很快的追溯到其根节点,这个特性对与并查集的find操作很方便,可以很容易判断一个节点是否在某一个集合中。如上图中的并查集,我们可以用下面的整形数组来表示
index : 1 2 3 4 5 6 7 8
data : 1 2 3 4 5 6 7 8
parent: 2 2 1 2 1 2 1 2
接下来我们再看一个例子,假设有10名罪犯,他们两两形成犯罪团伙,形成了5个等价对<A,B>,<C,K>,<J,F>,<H,E>,<D,G>(这里的等价关系可以理解为:A和B都是罪犯,那么认为他们是等价的)。以第一个等价对为例,<A,B>表示罪犯B由罪犯A领导,于是我们可以用树来产生的一个等价类集合,结构如下
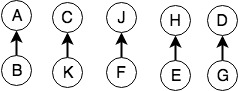
此时节点的值不再是整形,但仍然可以使用char型数组表示(父节点表示法):
index: 0 1 2 3 4 5 6 7 8 9
data: A B C K D E F G H J
parent: -1 0 -1 2 -1 8 9 4 -1 -1
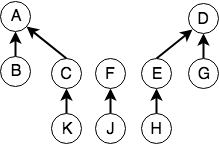
假如现在罪犯K和A相互勾结,E和G相互勾结,形成了两个新的犯罪团伙:(K,A) 和 (E,G)。以(K,A)为例,由于K的大哥是C,于是A提议让C也加入,形成一个更大的犯罪团伙,于是A,B,C,K形成了一个新的犯罪团伙,大哥为A。这个过程就是一个Union操作,我们合并了两个集合,得到了一个更大的集合,这个集合中的元素互为等价,他们拥有一个共同的根节点A,(E,G)类似。合并后的结构如下图
还是上面的例子,假如我们又新增加了一组等价对(H,J),由于J和H的大哥(根节点)不同,因此要将这两棵树做Union操作,根据上面规则,F有两个节点,D有4个节点,因此将F合并到D上(少数服从多数)。合并后的结构如下:
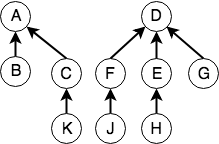
合并完我们发现原来5个小的犯罪团伙现在合并成两个大的了,对于警察来说,只需要找到其中任意一个小弟,即可找到这个犯罪团伙的大哥,例如,我们可以进行find(J)操作,则可根据J一路追溯到D。
总结一下,并查集其实就是为了将一组或几组数据进行归类,从而能够得到:
- 这些数据一共形成了多少个集合
- 对于数据中的每个元素,可以快速判断他们是否从属于同一类集合
上述两点比较抽象,在日常生活中的确有一些应用场景,比如用于判别网络结点间的连通性,给定若干个相连通的节点对,判断是否彼此连通,如果不连通,需要在哪些节点之间架设网络;再比如已知N个人相互之间的血缘关系,然后求有这N个人当中总共来自多少个家族;又或者计算社交网络中用户之间的关注关系等等。
并查集ADT
如果并查集中的节点是正整数,则可以使用一个int型的数组表示,如果节点为其它类型,则需要用一个泛型数组来表示,如下所示,其中ParTreeNode表示并查集中的节点,ParTree表示并查集
//树结点定义
template<class T>
class ParTreeNode {
private:
Tvalue; //结点的值
ParTreeNode<T>* parent; //父结点指针
int nCount; //集合中总结点个数
public:
ParTreeNode<T>* getParent(); //返回父结点指针
void setParent(ParTreeNode<T>* par); //设置父指针
};
// 树定义
template<class T>
class ParTree {
public:
ParTreeNode<T>* array; // 存储节点的数组
int Size; // 数组大小
ParTreeNode<T>* Find(ParTreeNode<T>* node) const; // 查找node结点的根结点
void Union(int i,int j); // 把下标为i,j的结点合并成一棵子树
// 判定下标为i,j是否在一个集合内
bool Connected(int i,int j){
return Find(array[i]) == Find(array[j]);
};
};
Find/Union操作
Find算法比较简单,对任意子节点,向上追溯父节点即可
template <class T>
ParTreeNode<T>* ParTree<T>::Find(ParTreeNode<T>* node) const{
ParTreeNode<T>* pointer=node;
while ( pointer->getParent() != NULL ){
pointer=pointer->getParent();
}
return pointer;
}
Union算法要考虑待合并的两棵树哪个节点多,将节点少的树合并到节点多的树上面
template<class T>
void ParTree<T>::Union(int i,int j) {
ParTreeNode<T>* pointeri = Find(&array[i]); //找到结点i的根
ParTreeNode<T>* pointerj = Find(&array[j]); //找到结点j的根
if (pointeri != pointerj) {
//检查个数
if(pointeri->getCount() >= pointerj->getCount()) {
pointerj->setParent(pointeri);
pointeri->setCount(pointeri->getCount() + pointerj->getCount());
}else{
pointeri->setParent(pointerj);
pointerj->setCount(pointeri->getCount() + pointerj->getCount());
}
}
}
路径压缩
由于find操作需要找到待查节点的根节点,需要遍历该节点的所有的父节点,当树很深时,效率是$O(n)$的,而实际上对该节点来说,它只需要找到它对应的根节点即可,并不关心它有多少个父节点,因此可以将它到根节点的路径缩短,即每个节点可维护一个直接指向其根节点的指针,这样整棵树就变矮了,产生了极浅树。
template <class T>
ParTreeNode<T>* ParTree<T>::FindPC(ParTreeNode<T>* node) const{
if (node->getParent() == NULL)
return node;
//对每个node,将其parent设为根节点
node->setParent(FindPC(node->getParent()));
return node->getParent();
}
使用路径压缩后的find操作时间复杂度可以达到$O(1)$。证明为:
- 对$n$个节点进行$n$次find操作的开销为$O(n\alpha(n))$, 约为$\Theta(n\log^{*}{}n)$
- $\alpha(n)$是单变量Ackermann函数的逆,它是一个增长速度比$\log{}n$慢得多但又不是常数的函数
- $\log^{*}{}n$ 是在 $n = \log{}n ≤ 1$ 之前要进行的对 $n$ 取对数操作的次数
- $\log^{*}65535=4$ (即当$n=65535$时,只需要4次$\log$操作,接近$O(1)$)
- Find至多需要一系列n个Find操作的开销非常接近于$\Theta(n)$,在实际应用中,$\alpha(n)$往往小于$4$
UnionFind的具体实现
为了便于理解,下面以一个整形数组为例,给出一种UnionFind的一种简单的实现方式
class QuickUF{
vector<int> roots;
public:
QuickUF(int N){
roots = vector<int>(N,0);
//创建N个节点个相互独立的节点,初始化父节点为自己
for(int i=0;i<N;i++){
roots[i] = i;
}
}
int findRoot(int i){
//为了路径压缩,暂时保留i
int root = i;
//1, 先找到根节点
while(roots[root] != root){
root = roots[root];
}
//2. 路径压缩,将i到根节点路径中所有节点的父节点更新为根节点
while(i!=root){
int tmp = roots[i];
roots[i] = root;
i = tmp;
}
return root;
}
//检查两个节点是否属于同一集合
bool connected(int p, int q){
return findRoot(p) == findRoot(q);
}
//合并两个集合
void union(int p, int q){
int proot = findRoot(p);
int qroot = findRoot(q);
roots[proot] = qroot;
}
};
字符树 Trie
对于前面提到的BST,当输入是随机的情况下,可能达到理想的查询速度O(log(N)),但是如果输入是有序的,则BST会退化为单链表,查询速度会降为O(N)。因此我们需要思考,对于BST的构建,能否不和数据的输入顺序相关,而和数据的空间分布相关,这样只要数据的空间分布是随机的,那么构建出的BST查询性能就会得到保证。
Trie树又称前缀树或字典树,它最早应用于信息检索领域,所谓”Trie”来自英文单词”Retrieval”的中间的4个字符”trie”。Trie的经典应用场景是搜索提示和分词,比如当我们在搜索栏中输入关键词时,地址栏会自动提示并补全关键字。在这个例子中,与之前BST搜索不同的是Trie中的节点保存的并不是key值,而是单个的英文字符,因此使用Trie检索某个字符串是否位于某个集合中,其过程是逐一检索字符串的每个前缀字符是否在Trie的节点中,而不是像BST一样直接比较字符串内容。如下图所示,我们可以将一组单词通过Trie树的形式进行构建,其中左图为等长字符串,每个字符均不是其它字符的前缀;右边为不等长字符串,每个字符可能是其它字符的前缀,这种情况我们需要在末尾增加一个*表示
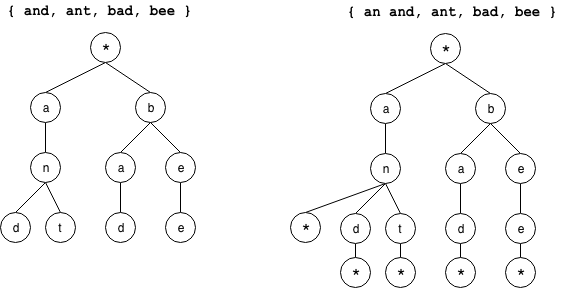
例如当我们想要查找字符串”bad”,我们只需要从Trie树的根节点开始依次匹配bad中的字符,直到遇到*表示匹配成功。
通过字符串查询的例子,我们可以看出,Trie树的特点是可以是对输入对象进行空间分解,一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie的实现
我们以字母树为例,介绍一种简单的Trie的实现方式。首先我们需要先定一个TrieNode的数据结构
struct TrieNode{
bool isEnd = false; //用来标识该节点是叶子节点
array<TrieNode*,26> children = {nullptr};
};
我们使用一个长度为26的静态数组来存储其孩子节点,如果某个位置不为空则说明该位置有一个孩子节点,可参考下图:
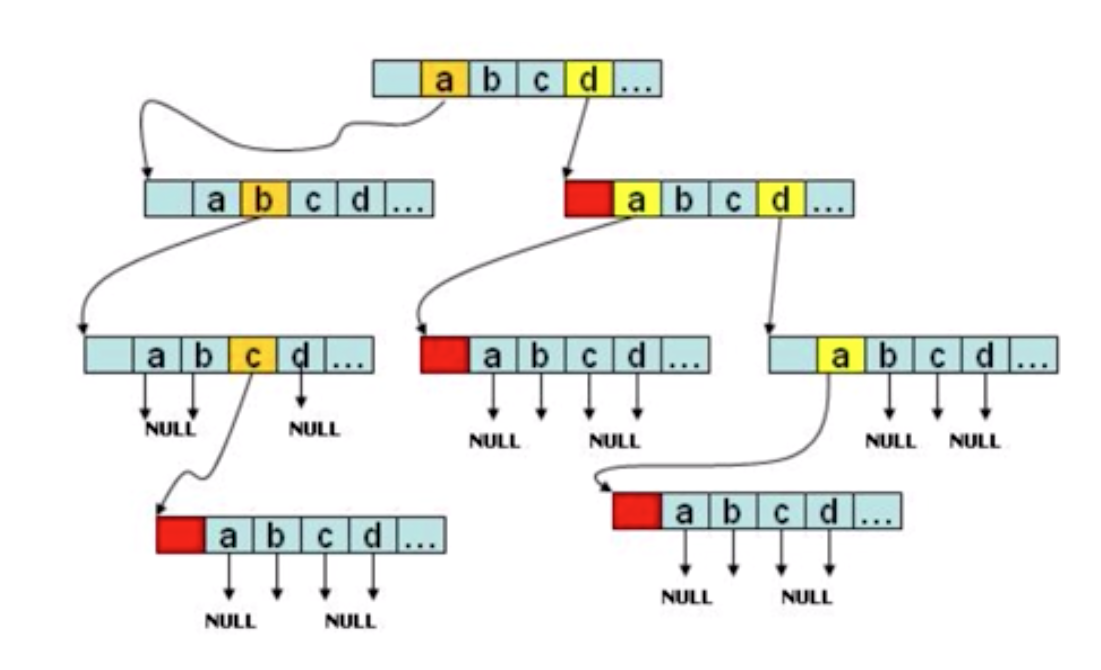
接下来我们可以实现Trie的类
class Trie {
TrieNode* root;
public:
Trie() {
root = new TrieNode();
}
~Trie(){
delete root;
root = nullptr;
}
void insert(string word) {
TrieNode* node = root;
for(int i =0; i<word.size(); i++){
int index = word[i]-'a';
TrieNode* n = node->children[index];
if(!n){
node->children[index] = new TrieNode();
node = node->children[index];
}else{
node = n;
}
}
node->isEnd = true;
}
bool search(string word) {
TrieNode* node = root;
for(int i=0;i<word.size();i++){
int index = word[i]-'a';
TrieNode* n = node->children[index];
if(!n){
return false;
}else{
node = n;
}
}
return node->isEnd;
}
bool startsWith(string prefix) {
TrieNode* node = root;
for(int i=0;i<prefix.size();i++){
int index = prefix[i]-'a';
TrieNode* n = node->children[index];
if(!n){
return false;
}else{
node = n;
}
}
return true;
}
};
Trie的最大优点是最大限度减少无效的字符串比较,其核心思想是利用空间换时间,即利用字符串的公共前缀来降低查询时间的开销,以达到提高效率的目的。那么在Trie树中,检索一个字符串时间复杂度是多少呢?正如前文所述,Trie树集中应用的场景是关键词检索,如果需要在一组字符串中检索某些字符串,使用Trie会非常的高效。构建Trie需要扫描所有字符串,因此时间复杂度为O(n),n为所有字符串长度总和。一旦Trie构建完成,后续的查询某个串的时间复杂度为O(k),k为要查找字符串长度。在实际的应用中,Trie的实现往往不是上面那么简单,我们可以有很多种优化方式来减少Trie的空间占用,比如可以对只有一个孩子的节点进行合并等。
Trie树的缺点是应用场景有限,相比于哈希表,红黑树等高效的动态检索数据结构,Trie对要处理的字符串有着严苛的要求。
- Trie中包含的字符集不能太大,如果字符集太大,存储空间会被浪费很多
- 要求字符串的前缀重合比较多,不空间消耗会变大很多
- 标准库中不提供Trie的实现,实际应用中需手写,成本较高
综合这几点,针对在一组字符串中查找特定字符串的问题,在工程中更倾向于使用散列表或者红黑树,这两类数据结构一般程序语言的标准库均有提供。Trie虽然不适合精确匹配字符串,但对于需要检索前缀的场景却是最适合不过了。
