图（一）

Posted on 2008-09-10 | In DataStructure

术语

图的定义

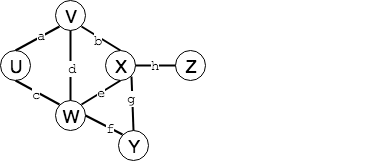
数学意义的图包含两个元素 $G=(V,E)$，顶点集合 $n = | V |$，边集合 $ e= | E | $。假设一个图有三个顶点，彼此连通，则$V=\{v_0,v_1,v_2\}$，$E=\{(v_1,v_2),(v_1,v_3),(v_2,v_3)\}$。

邻接关系/关联关系

可以被边相连的两个点成为邻接关系(adjacency)，邻接关系是顶点与顶点之间的关系，顶点与某条边之间的关系称为关联关系(incidence)

路径

路径为一系列的顶点按照依次邻接的关系组成的序列，*$\pi = <v_0,v_1…,v_k>$，长度$|\pi|=k$。如上图中$V$到$Z$的一条路径为${b,h}$或${V,X,Z}$。路径的长度为顶点的个数或者边的个数。如果再一条通路中不含重复节点，我们称之为 简单路径 ($v_i = v_j$除非$i=j$)。

连通图

若图中任意两点都是连通的，那么该图称为连通图。对于有向图 $G (V,E)$，如果两个顶点 $v_i,v_j$ 间有一条从$v_i$ 到 $v_j$ 的有向路径，责成同时还有一条从 $v_j$ 到 $v_i$ 的有向路径，则称两个顶点强连通,称$G 为强连通图。强连通图只有一个连通分量，即其自身。

环路

当路径的起点和终点重合时，称之为环路($v_0=v_k$)。如果再有向图中不包含任何环路，则称之为有向无环图(DAG,Directed Acyclic Graph)，树和森林是 DAG 图的一种特例。对于只有两个顶点的图，如果是无向图，则不认为是环路；如果是有向图，且两个顶点之间有两条边，则认为是环路，例如$<v_0,v_1>$和$<v_1,v_0>$构成环

无向图/有向图

若邻接顶点$u$和$v$的次序无所谓，则$(u,v)$为无向边(undirected edge)，若图中的所有边均为无向边，则这个图称为无向图。反之，有向图(digraph)中均为有向边(directed edge)，$u,v$分别称作边$(u,v)$的尾，头，表示从$u$出发，到达$v$。

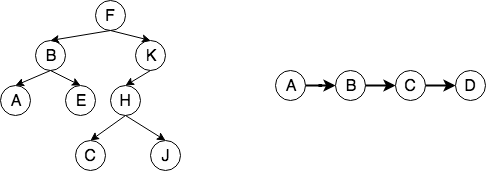
之前介绍的数据结构都可以看成是图的一种表现形式，比如二叉树是一种无权的有向无环图，节点的入度为 1，出度最大为 2，顶点之间只有一条路径。而单项链表也可以看成是一种无权的 DAG，每个节点的入度出度都为 1

图的表示

上面我们已经了解了关于图的逻辑模型和基本接口，但是在计算机中该如何表示这个模型呢？方法有很多种，这里我们主要介绍三种，分别是边表(edge list)，邻接矩阵(adjacency matrix)和邻接表(adjacency list)。

边表

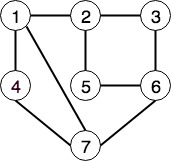
边表，顾名思义是使用一个无序链表来表示图，其中链表中的每个节点为一组边的集合。如上图中，我们可以使用如下链表来表示图:

(1,2)

(1,4)

(1,7)

(2,3)

(2,5)

(3,6)

(4,7)

(5,6)

(5,7)

(6,7)

对于每个节点的有序对，使用起点和终点来表示方向，值为顶点的内容。因此这种表示方法不会显示的存放顶点，所有顶点信息均包含在边表中。

edge_list = [ [1,2],[1,4],[1,7],...,[6,7]]

显然这种方式对顶点操作不是很友好，如果想要找出4的邻居节点，则要遍历每个节点，不是很高效。

邻接矩阵/关联矩阵

所谓邻接矩阵就是描述顶点之间链接关系的矩阵。设$G=<V,E>$是一个有$n$个顶点图，则邻接矩阵是一个$n \times n$的方阵，用二维数组A[n,n]表示，它的定义如下:

\[A[i,j]= \begin{cases}\ 1, \qquad 若(v_i, v_j)∈ E 或<v_i, v_j> ∉ E \\ 0, \qquad 若(v_i, v_j)∈ E 或<v_i, v_j> ∉ E \\ \end{cases}\]

如果顶点$i,j$相连，对于无向图，则$A[i,j]$和$A[j,i]$的值相同；对于有向图，则分别对应各自的$A[i,j]$和$A[j,i]$的值；如果是带权图，则矩阵中元素的值为权值$w$。

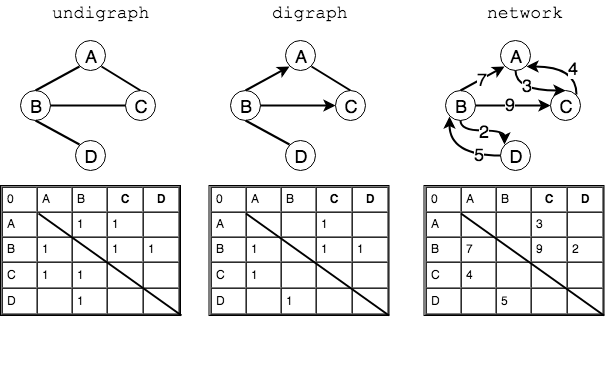
可见，对于一个$n$个顶点的图，邻接矩阵是一个对称阵（默认不考虑自环的情况，因此对角线的元素值为 0)，空间代价为$O(n^2)$。

基于邻接矩阵的图结构，可以用二维数组来表达：

class Graph{
private:
    vector<Vertex* > V; //顶点
    vector<vector<Edge<Te>*>> matrix; //边集合，邻接矩阵
    //map<Vertex* , vector<Edge* >> matrix; //也可以使用map
    //map<Vertex* , set<Edge* >> matrix; //也可以使用map
};

使用邻接矩阵的优点是：

直观，易于理解和实现
适用范围广，包括有向图，无向图，带权图，自环图等等，尤其适用于稠密图
判断两点之间是否存在联边: $O(1)$
获取顶点的出度入度: $O(1)$
- 添加删除边后更新度: $O(1)$
扩展性强

缺点为：

空间复杂度为$\Theta(n^2)$，与边数无关

以左边无向图的邻接矩阵为例，Python 表示如下：

adjacency_matrix = [
    #v0,v1, v2,  v3
    [0, 1,  1,  0], #v0
    [1, 0,  1,  1], #v1
    [1, 1,  0,  0], #v2
    [0, 1,  0,  0]  #v3
]

邻接表

对于任何一个矩阵，我们以定义它的稀疏因子：在$m \times n$的矩阵中，有$t$个非零单元，则稀疏因子$\delta$为

\[\delta = \frac{t}{m \times n}\]

若$\delta < 0.05$，可认为是稀疏矩阵。对于稀疏图，边较少，邻接矩阵会出现大量的零元素，耗费大量的存储空间和时间，因此可以采用邻接表存储法。

邻接表(adjacency list)采用的是链式存储结构，它为顶点和边各自定义了一个结构，对于顶点包含两部分：

存放该节点$v_i$的数据域
指向第一条边对象的指针

对于边结构包含三部分:

与顶点$v_i$临街的另一顶点的序号
顶点$v_i$下一条边的指针
权重值(可选)

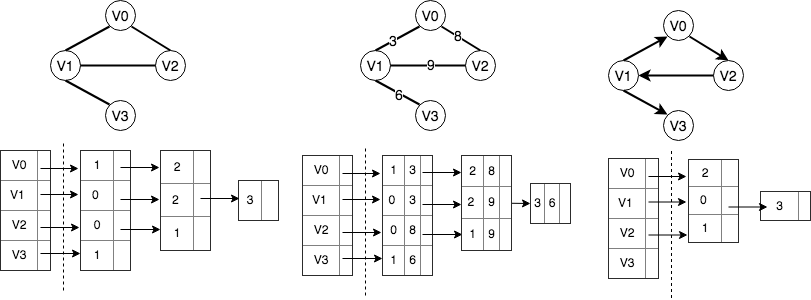
上图分别为无向图，带权图和有向图的邻接表，对于有向图，有出度和入度两种邻接表，这里只给出了出度的邻接表，对于入度的情况类似。由上图的结构可以看出使用邻接表，对每个节点的相邻节点的访问是非常高效的，另外，邻接表的空间利用率也相对较高。以左边无向图的邻接表为例，Python 表示如下：

#使用list
adjacency_list = [
    [1,2], #v0
    [0,2,3], #v1
    [0,1], #v2
    [1,1] #v3
]
#也可以使用kev,value对表示
adjacency_map = {
    0: [1,2],
    1: [0,2,3],
    2: [0,1],
    3: [1,1]
}

基于邻接表的无向图的 C++代码表示如下:

class Graph {
    int n; //顶点个数
    vector<vector<int>> adj; //邻接表
public:
    Graph(int n){
        this.n = n;
        adj = vector<<vector<int>>(n,vector<int>());
    }
    void addEdge(int s, int t){
        //无向图一条边存两次
        adj[s].push_back(t);
        adj[t].push_back(s);
    }
}

几种图的不同实现方式的性能比较

	边表	邻接表	邻接矩阵
内存消耗	$V+E$	$V+E$	$V^2$
判断相邻节点	$E$	$degree(v)$	V
添加顶点	$1$	$1$	$V^2$
删除顶点	$E$	$1$	$V^2$
添加边	$1$	$1$	$1$
删除边	$E$	$degree(v)$	1

图的搜索与遍历

在图中搜索两点间的路径有很多种方式，常用的有 DFS，BFS，Dijkstra，A*等，对于图的遍历，和树类似我们也可以使用 DFS 和 BFS 两种方式，但是图有两个树没有的问题：

连通的问题，从一个点出发不一定能够到达所有点，比如非连通图
可能存在回路，因此遍历可能进入死循环

解决这两个问题，需要给顶点加一个状态位，标识该节点是否已经被访问过。另外，对图的遍历，可将其按照一定规则转化为对树的遍历

void graph_traverse(){
    // 对图所有顶点的标志位进行初始化
    for(int i=0; i<VerticesNum(); i++)
        status(V[i]) = UNVISITED;
        // do_traverse函数用深度优先或者广度优先
        do_traverse(v);
    }
}

DFS

图的 DFS 遍历过程和之前介绍的树的 DFS 遍历过程类似，都是从一个节点开始，不断的递归+回溯，最终走完全部路径。其基本步骤为

选取一个未访问的点$v_0$作为源点,访问顶点$v_0$
若$v_0$有未被访问的邻居，任选其中一个顶点$u_0$，进行递归地深搜遍历；否则，返回
顶点$u_0$，重复上述过程
不断递归+回溯，直至所有节点都被访问

//dfs遍历伪码
void dfs(Vertex v) { // 深度优先搜索的递归实现
    status(v) = VISITED;  // 把标记位设置为 VISITED
    Visit(v); // 访问顶点v
    //访问所有UNVISITED状态的节点
    for(auto u : getNbrs(v))
        if (status(u) == UNVISITED){
            dfs(u);
        }
    }
}

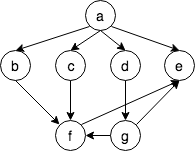
例如上图 DFS 的遍历次序为：a b c f d e g。这里有一点要注意，由于第二步对相邻节的未访问的节点选取规则不唯一（下图例子使用的是字母顺序），因此对全图进行遍历得到结果序列是不唯一的。类似的，如果使用 DFS 进行搜索，寻找两点间路径，得到的结果不一定是最短路径。dfs 的搜索代码如下

void dfs(int s, int t){
    bool found = false;
    //记录访问过的顶点
    vector<bool> visited(n,false);
    //记录前驱节点，创建n个桶
    vector<int> prev(n,-1);
    //调用一个辅助函数
    helper(s,t,visited,prev,found);
    if(found){
        print_path(prev,st,);
    }
}
void helper(int s, int t, vector<bool>& visisted, vector<int>& prev, bool& found){
    if(found == true){
        return ;
    }
    visited[s] = true;
    if(s == t){
        found = true;
        return;
    }
    for(int i=0;i<adj[s].size();i++){
        int x = adj[s][i];
        if(!visited[x]){
            //记录前驱节点
            prev[x] = s;
            helper(x,t,visited,prev,found);
        }
    }
}
//打印路径
void print_path(vector<int>& prev, int s, int t){
    if(!prev[t] != -1 && t != s){
        print_path(prev,s,prev[t]);
    }
    cout<<t<<" ";
}

BFS

图的广度优先遍历过程类似从某个点出发，一圈一圈的向外层顶点扩散的过程

从图中的某个顶点$v_0$出发，访问并标记该节点
依次访问$v_0$所有尚未访问的邻接顶点
依次访问这些邻接顶点的邻接顶点，如此反复
直到所有点都被访问过

//bfs遍历伪码
void BFS(Vertex v) {
    status(v) = VISITED;
    queue<Vertex> Q; // 使用STL中的队列
    Q.push(v); // 标记,并入队列
    while (!Q.empty()) { // 如果队列非空
        Vertex v = Q.front (); // 获得队列顶部元素
        Q.pop(); // 队列顶部元素出队
        Visit(u);//访问节点
        //遍历v的每一个未被访问的相邻节点
        for(auto u : getNbrs(v)){
            if (status(u) == UNVISITED){
                status(u) = VISITED;
                u.previous = v;//设置前驱节点
                Q.push(u);
            }
        }
    }
}

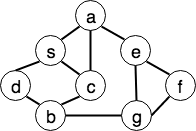
以上图为例，假设我们从s开始遍历：

随机选取一个s节点，入队
s出队并做标记,将s的相邻节点a,c,d，入队
a出队并做标记,将a相邻节点入队，由于s,c已经是被标记，于是只有e入队
同理，c出队，b入队，以此类推
直至节点全部被访问

对于无权图来说，BFS 相比 DFS 可以用来寻找两点间（例如上图中的 a 和 b）的最短路径（最少边），但却不容易保存到达 b 点的路径，解决这个问题，可以给每个节点加一个指向前驱节点的指针，或者使用一个数组存储中间节点，代码如下：

//起点s，终点t，顶点个数n
void bfs_search(int s, int t){
    if(s == t){
        return;
    }
    //记录访问过的顶点
    array<bool,n> visited = {false};
    visited[s] = true;
    queue<int> q;
    q.push(s);
    //记录前驱节点，创建n个桶
    vector<int> prev(n,-1);
    while(!q.empty()){
        int x = q.front();
        q.pop();
        visited[x] = true;
        //访问x的邻接顶点
        for(int i=0;i<adj[x].size();i++){
            int y = adj[w][i];
            if(!visited[y]){
                //记录y的前驱为x
                prev[y] = x;
                //找到目标节点
                if(t == y){
                    print_path(prev,s,t);
                    return;
                }
                q.push(y);
            }
        }
    }
}

下面我们来分析一下时间复杂度，DFS 和 BFS 每个顶点访问一次，对每一条边处理一次 (无向图的每条边从两个方向处理)

采用邻接表表示时，有向图总代价为 $\Theta(n + e)$，无向图为 $\Theta(n + 2e)$
采用相邻矩阵表示时，理论上，处理所有的边需要 $\Theta(n^2)$的时间，所以总代价为$\Theta(n + n^2) = \Theta(n^2)$。但实际上，在执行nextNbr(v,u)时，可认为是常数时间，因此它的时间复杂度也可以近似为$\Theta(n + e)$

广度优先搜索和深度优先搜索是图上的两种最常用、最基本的搜索算法，比起其他高级的搜索算法，比如 A、IDA 等，要简单粗暴，没有什么优化，所以，也被叫作暴力搜索算法。所以，这两种搜索算法仅适用于状态空间不大，也就是说图不大的搜索。在下一篇文章中，我们会继续介绍几种带权图的搜索方法以及图相关的其它内容

LeetCode Problems

接下来我们来看下 Leetcode 中的一些经典 Graph 的问题

Clone Graph

这个题目的意思是给一个 Graph Node，让我们完成对这个 Graph 的 deep copy。这里 Graph 是一个有无环图，因此我们需要递归的拷贝每个 neighbor 节点，由于每个节点可能被访问多次，因此，为了避免重复拷贝，我们需要用一个 hashmap 记录已经拷贝的节点: map<oldNode: newNode>

"""
# Definition for a Node.
class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []
"""

from typing import Optional

# the trick is to use a hashmap to store the nodes that have already been cloned
# key: old node, value: new node
class Solution:
    def recursiveColone(self, node: Optional['Node'], cache) -> Optional['Node']:
        if node is None:
            return None
        # if node is in the cache
        if node in cache:
            return cache[node]

        newNode = Node(node.val, [])
        cache[node] = newNode
        for node in node.neighbors:
            newNode.neighbors.append(self.recursiveColone(node, cache))
        return newNode

    def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
        cache = {}
        return self.recursiveColone(node, cache)