图（二）

Dijkstra算法

路径的权值在某些场合下是非常重要的，比如两地间飞机的票价，两个网络节点间数据传输的延迟等等。DFS和BFS在搜索两个节点路径时不会考虑边的权值问题，如果加入权值，那么两点间权值最小的路径不一定是BFS得到的最短路径，如下图中求$\{a,f\}$两点间的BFS的结果为$\{a,e,f\}$，cost为9，而cost最少的路径为$\{a,d,g,h,f\}$，其值为6

Dijkstra算法研究的是单源最短路径(single-source shortest paths)问题，即给定带权图 G = <V,E>，其中每条边 $(v_i，v_j)$ 上的权 $W[v_i，v_j]$ 是一个非负实数。计算从任给的一个源点s到所有其他各结点的最短路径。

Dijkstra算法的基本思想是使用贪心法维护一个数据结构，记录当前两点间的最短路径，然后不断更新路径值，直到找到最终解。

function dijkstra(v1,v2):
    //初始化所有节点的cost值
    for v in all vertexes{
        v.cost = maximum
    }
    v1.cost = 0
    //创建一个最小堆保存顶点，优先级最低的顶点在堆顶部
    priority_queue pq(v1.cost);

    while !(pq.empty()){
        v = pq.front(); //弹出优先级最低的vertex
        v.status = visited
        if v == v2:
            //找到v2
            break;
        //遍历v的每一个未被访问的相邻节点
         for n : v.unvisited_neighbors:
            //计算到达n的cost
            cost := v.cost + weight of edge(v,n)
            if cost < n.cost:
                n.cost = cost
                //记录前驱节点
                n.prev = v
                pq.push( n.cost )
    }
    //使用v2的前驱节点，重建到v1的路径

上述是Dijkstra算法的伪码，我们通过下面一个例子看看它是如何工作的。如下图所示，假设我们要求从$\{a,f\}$的权值最短路径。

1. 初始化各节点的cost为无穷大，令a的cost为0，放入优先级队列pq

2. 从pq中取出顶部节点，访问它的相邻节点b,d，计算到达b,d的cost，分别为2,1，由于2,1均小于b,d原来的cost(无穷大)，因此将b,d的cost更新，放入到优先队列，第一次选择（循环）结束，此时队列中的顶点为pqueue = {d:1,b:2}

3. 重复步骤2，pq顶部的节点为d,找到d相邻的节点c,f,g,e分别计算各自的权重为3,9,5,3，均小于各自cost值（无穷大），因此c,f,g,e入队，第二次循环结束，此时队列中的顶点为pqueue = {b:2,c:3,e:3,g:5,f:9}

4. 重复步骤2，pq顶部的节点为b，找到b相邻的节点d,e，由于d在上一步中已经被访问了，于是略过d，计算b到e的cost为2+10=12，大于e在上一步得到的cost3，因此直接返回。第三次循环结束，此时队列中的顶点为pqueue = {c:3,e:3,g:5,f:9}

5. 重复步骤2，pq顶部的节点为c,找到d相邻的节点f，计算到达f的权重为8，小于队列中的9，说明该条路径优于第三步产生的路径，于是更新f的cost为8，更新f的前驱节点为c。第四次循环结束，此时队列中的顶点为pqueue = {e:3,g:5,f:8}

6. 重复步骤2，pq顶部的节点为e，找到e相邻的节点g，计算e到g的cost为3+6=9，大于g在之前得到的cost5，因此直接返回。第五次循环结束，此时队列中的顶点为pqueue = {g:5,f:8}

7. 重复步骤2，pq顶部的节点为g，找到g相邻的节点f，计算g到f的cost为5+1=6，小于f在之前得到的cost8，说明从g到达f这条路径更优，于是更新f的cost为6，更新f的前驱节点为g，此次循环结束，此时队列中的顶点为pqueue = {f:8}

8. 重复步骤2，发现已经到达节点f因此整个循环结束。然后从f开始根据前驱节点依次回溯，得到路径f<-g<-d<-a，为权值最优路径。

从上面的求解过程可以发现Dijkstra算法实际上是一种贪心算法，即每一步都找当前最优解（最小堆堆顶元素)。对于贪心法，它实际上是动态规划算法的特例，因此要求每一步的重复子结构解具有无后效性。对应到Dijkstra算法，要求路径的权值不能为负数。因为如果出现负数，当前的最优选择在后面不一定是最优。

• Dijkstra算法时间复杂度

对于稀疏图，Dijkstra算法使用最小堆实现效率较高：

1. 初始化: $O(v)$
2. While循环： $O(v)$
   • remove vertex from pq: $O(\log{V})$
   • potentially perform E updates on cost/previous
   • update costs in pq: $O(\log{V})$
3. 路径重建： $O(E)$
4. 总的时间复杂度为: $O(V\log{V}+E\log{V}) = O(E\log{V})$ (如果图是连通的，有$V=O(E)$)

A* 算法

A*是另一种寻找权值最优路径的方法，它是对Dijkstra算法的一种改进。Dijkstra虽然可以找到最短路径，但是BFS的寻找过程却不是最高效的，如下图所示

假设我们要从中心点走到最右边的点，由于从中心扩散出去的每个点权值都相同，Dijkstra算法会在四个方向上不断尝试每个扩散出去的点，显然，这种搜法包含大量的无效搜索。仔细思考不难发现，其原因在于Dijkstra算法基于贪心策略每次只能确定当前最短距离，而不知道哪个方向才能逼近终点，如下图中，Dijkstra每次只能确定由a节点确定b节点，而对于终点c在哪则毫无所知，没有任何信息：

针对这个问题，A*算法改进了Dijkstra，引入了一个Heuristic的估计函数来来确定节点的扩散方向，使其可以沿着终点方向逼近，如下图所示

在引入了一个Heuristic函数后，我们相当于知道了一些额外的信息，这些信息可以帮助我们减少不必要的搜索。假设我们想要找从a到c的权值最小路径，对于任何中间节点b，我们要计算两个值

1. 从a到b确定的权值(同Dijkstra)
2. 从b到c的估计值（estimated cost）

A*的整体算法框架同Dijkstra相同，只需要将最小堆中存放的cost改为cost(n) + H(n,target)即可

v1.cost = H(v1,v2)
priority_queue pq(v1);
//...
pq.push( n.cost + H(n,v2) )

A* 算法的难点在于如何找到合适的Heuristic函数，不同的搜索场景，使用的Heuristic也不相同，例如下面场景，我们希望从a走到c:

此时可以将Heuristic函数定义为:H(p1,p2) = abs(p1.x-p2.x) + abs(p1.-p2.y)，则根据这个公式计算出的cost值如上图中每个格子所示，可以看到，从a点扩散出去的节点不再是等cost的，而是越偏向c点，cost的值越低。

关于Heuristic函数有一点需要特别注意的是，对终点cost的估计不能over estimate，也就是估计出来的值比实际值要大很多，这样会导致真实的最短路径一直被压在最小堆中，产生不必要的冗余计算。虽然Heuristic函数不可以over estimate，但是却可以under estimate。

最后我们以一个迷宫的例子来直观的比较一下Dijkstra和A*算法的效率，如下图所示，左边为Dijkstra算法结果，需要走103步，右边是A*算法，只需要25步（图中格子之间路径的cost均为1）

最小生成树

所谓生成树(Spanning Tree)是连接无环图中所有顶点的边的集合。如下图所示，我们将左边的图去环后得到了右边的无环图，该图即是一棵生成树

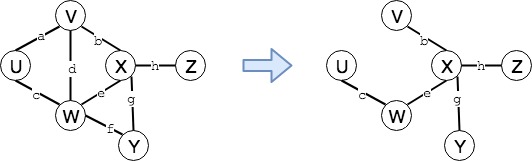
所谓最小生成树，是图中所有生成树中权值之和最小的一棵,简称 MST(minimum-cost spanning tree)。

• Kruskal’s algorithm

Kruskal算法是一种贪心算法，主要步骤如下：

1. 将图$G$中所有边放入最小堆$E$
2. 删除图$G$中的所有边，剩下$n$个顶点，此时图的状态为无边的森林$T=<V,{}>$
3. 在$E$中弹出权值最小边，如果该边的两个顶点在$T$中不连通，则将其加入到$E$中，否则忽略这条边
4. 依次类推，直到$E$为空，此时就得到图$G$的一颗最小生成树

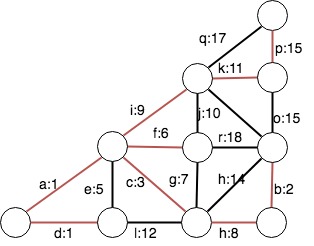
如上图所示，首先将所有边放入优先队列，则权值最小的a在堆顶，然后a出队，其两个顶点不连通，因此将该边放入图中（标红），当e出队的时候，我们发现e的两个顶点可以已通过a,d连通，因此e被忽略。按照此规则，以此类推，最终得到最小生成树（图中红色边）为:a,b,c,d,f,h,i,k,p总权值为1+2+3+4+6+8+9+11+16 = 60。不难看出，上述规则依旧是贪心法，每次选择权值最小的路径，其伪码如下：

function kruskal(graph):
    //创建一个最小堆
    priority_queue pq
    //将图中所有边放最小堆中，则权值cost最小的边在堆顶
    for edge : graph.all_edges:
        pq.push(edge) 
    //此时产生n个顶点，对应n个等价类
    while equal_num > 1: //等价类个数>1,说明还没有形成树
        //循环
        while not pq.empty():
            e = pq.front()
            pq.pop()
            v1 = e.from()
            v2 = e.to()
            //如果v1，v2两点不连通，则把该边放入图中，否则忽略这条边
            if graph.different(v1, v2): //判断v1,v2是否不连通
                graph.union(v1,f2); //合并两个顶点所在的等价类
                //将该条边放入图中
                graph.addEdge(v1,v2)
                //等价类个数-1
                equal_num -= 1

Kruskal算法使用了路径压缩（并查集）来合并等价类，different() 和 Union() 函数几乎是常数。假设可能对几乎所有边都判断过了，则最坏情况下算法时间代价为$\Theta(e\log{e})$，即堆排序的时间,通常情况下只找了略多于 n 次，MST 就已经生成，因此，时间代价接近于$\Theta(e\log{e})$

• Prim’s algorithm

Prim算法和上面算法类似，也是采用贪心的策略，不同的是Prim算法每次取权值最小边对应的顶点，具体如下（代码见附录）：

1. 从图中任意一个顶点开始 (例如A)，首先把这个顶点包括在MST中
2. 然后从图中选一个与A点连通，但不再MST中的顶点B，并且A到B的权值最小的一条边连同B一起加入到MST中
3. 如此进行下去，每次往 MST 里加一个顶点和一条权最小的边，直到把所有的顶点都包括进 MST 里
4. 算法结束时, MST中包含了原图中的n-1条边

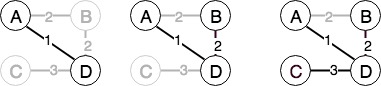
Prim 算法非常类似于 Dijkstra 算法，算法中的距离值不需要累积，直接用最小边，而确定代价最小的边就需要总时间$O(n^2)$；取出权最小的顶点后，修改 D 数组共需要时间$O(e)$，因此共需要花费$O(n^2)$的时间。Prim算法适合于稠密图，对于稀疏图，可以像 Dijkstra 算法那样用堆来保存距离值。

拓扑排序

所谓拓扑排序，是一种对有向无环图顶点排序的方式，排序的规则为两个顶点之间的前后位置，比如从顶点$v_i$到顶点$v_j$有一条有向边$(v_i, v_j)$，那么我们认为$v_i$在$v_j$的前面。

生活中有很多拓扑排序的场景，比如任务之间的依赖关系，学生的选课等，以选课为例，假如我们有如下课程，它们之间的依赖关系为：

如下图所示，如果我们要修完图表中的课程，我们该按照怎样的顺序选课，才能保证课程能够正常修完呢(在修某一门课程前，要先修完它的先序课程)？我们可以首先按照节点间的先决条件（课程之间的关联关系）来构建一个有向无环图图，如图(a)所示，然后将图(a)等价的转化为图(b)，显然，图(b)就是一份可行的选课顺序。

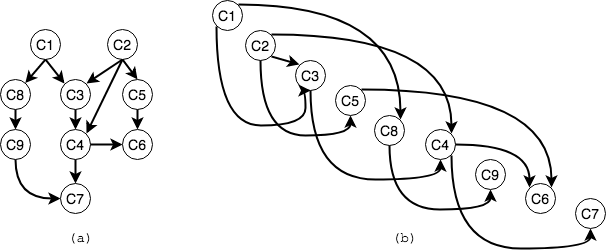
实际上，许多应用问题，都可转化和描述为这一标准形式：给定描述某一实际应用的有向图（图(b)），如何在与该图“相容”的前提下，将所有顶点排成一个线性序列（图(c)）。此处的“相容”，准确的含义是：每一顶点都不会通过边，指向其在此序列中的前驱顶点。这样的一个线性序列，称作原有向图的一个拓扑排序（topological sorting）。

对于有向无环图，它的拓扑序列必然存在，但是却不一定唯一，如上面的例子，$C_1$,$C_2$互换后，仍然是一个拓扑排序。我们可以一种BFS遍历的方式来得到这样一组拓扑序列，方法如下

1. 从图中选择任意一个入度为0的顶点且输出
2. 从图中删掉此顶点及其所有的出边，则其所有相邻节点入度减少1
3. 回到第 1 步继续执行

void TopsortbyQueue(Graph& G) {
    for (int i = 0; i < G.VerticesNum(); i++)
        G.status(G.V[i]) = UNVISITED; // 初始化
    }
    queue<Vertex<int>> Q; // 使用STL中的队列
    for (i = 0; i < G.VerticesNum(); i++){ // 入度为0的顶点入队
        if (G.V[i].indegree == 0) {
            Q.push(i);
        }
    }
    while (!Q.empty()) { // 如果队列非空
        Vertex<int> v = Q.front(); 
        Q.pop(); // 获得队列顶部元素， 出队
        Visit(G,v); 
        G.status(v) = VISITED; // 将标记位设置为VISITED
        for (Edge e = G.FirstEdge(v); G.IsEdge(e); e = G.NextEdge(e)) {
            Vertex<int> v = G.toVertex(e);
            v.indegree--; // 相邻的顶点入度减1    
        if (v.indegree == 0){ // 顶点入度减为0则入队
            Q.push(v);
        } 
    }
    for (i = 0; i < G.VerticesNum(); i++){ // 判断图中是否有环
        if (G.status(V[i]) == UNVISITED) {
            cout<<“ 此图有环！”; break;
        }
    }
}

Resources

• A* Algorithm For Beginners
• Introduction to A*
• CS106B-Stanford-YouTube
• Algorithms-Stanford-Cousera
• 算法与数据结构-1-北大-Cousera
• 算法与数据结构-2-北大-Cousera
• 算法与数据结构-1-清华-EDX
• 算法与数据结构-2-清华-EDX
• 算法设计与分析-1-北大-Cousera
• 算法设计与分析-2-北大-EDX

附录1

• Kruskal’s algorithm

void Kruskal(Graph& G, Edge* &MST) { // MST存最小生成树的边
    ParTree<int> A(G.VerticesNum()); // 等价类
    MinHeap<Edge> H(G.EdgesNum()); // 最小堆
    MST = new Edge[G.VerticesNum()-1]; // 为数组MST申请空间
    int MSTtag = 0; // 最小生成树的边计数
    for (int i = 0; i < G.VerticesNum(); i++) // 将所有边插入最小堆H中
        for (Edge e = G. FirstEdge(i); G.IsEdge(e); e = G. NextEdge(e))
            if (G.FromVertex(e) < G.ToVertex(e))// 防重复边
                H.Insert(e);
    int EquNum = G.VerticesNum(); // 开始有n个独立顶点等价类
    while (EquNum > 1) { // 当等价类的个数大于1时合并等价类
        if (H.isEmpty()) {
            cout << "不存在最小生成树." <<endl;
            delete [] MST;
            MST = NULL; // 释放空间
            return;
        }
        Edge e = H.RemoveMin(); // 取权最小的边
        int from = G.FromVertex(e); // 记录该条边的信息
        int to = G.ToVertex(e);
        if (A.Different(from,to)) { // 边e的两个顶点不在一个等价类
            A.Union(from,to); // 合并边的两个顶点所在的等价类
            AddEdgetoMST(e,MST,MSTtag++); // 将边e加到MST
            EquNum--; // 等价类的个数减1
        }
    }
}

• Prim’s algorithm

void Prim(Graph& G, int s, Edge* &MST) { // s是始点，MST存边
    int MSTtag = 0; // 最小生成树的边计数
    MST = new Edge[G.VerticesNum()-1]; // 为数组MST申请空间
    Dist *D;
    D = new Dist[G. VerticesNum()]; // 为数组D申请空间
    for (int i = 0; i < G.VerticesNum(); i++) { // 初始化Mark和D数组
        G.Mark[i] = UNVISITED;
        D[i].index = i;
        D[i].length = INFINITE;
        D[i].pre = s; // D[i].pre = -1 呢？
    }
    D[s].length = 0;
    G.Mark[s]= VISITED; // 开始顶点标记为VISITED
    int v = s;
    for (i = 0; i < G.VerticesNum()-1; i++) {// 因为v的加入，需要刷新与v相邻接的顶点的D值
        for (Edge e = G.FirstEdge(v); G.IsEdge(e); e = G.NextEdge(e))
            if (G.Mark[G.ToVertex(e)] != VISITED &&(D[G.ToVertex(e)].length > e.weight)) {
                D[G.ToVertex(e)].length = e.weight;
                D[G.ToVertex(e)].pre = v;
            }
            v = minVertex(G, D); // 在D数组中找最小值记为v
            if (v == -1) return; // 非连通，有不可达顶点
            G.Mark[v] = VISITED; // 标记访问过
            Edge edge(D[v].pre, D[v].index, D[v].length); // 保存边
            AddEdgetoMST(edge, MST, MSTtag++); // 将边加入MST
    }
}
int minVertex(Graph& G, Dist* & D) {
    int i, v = -1;
    int MinDist = INFINITY;
    for (i = 0; i < G.VerticesNum(); i++){
        if ((G.Mark[i] == UNVISITED) && (D[i] < MinDist)){
            v = i; // 保存当前发现的最小距离顶点
            MinDist = D[i];
        }
    }
    return v;
}