B/B+树 和 红黑树
动态索引
动态索引主要用于处理索引结构本身可能发生变化的场景,比如数据库中的primary key可能会频繁插入,删除,造成索引结构的频繁更新。建立动态索引的目的视为了保持较好的查询性能,提高检索效率。常用的动态索引结构有B/B+树,红黑树等。
B树
B树是R.Bayer和E.MacCreight在1970年提出的一种平衡的多路查找树。所谓的多路搜索树和前面提到的二路搜索树实际上是等价的,只需要将BST的父节点和子节点进行合并即可得到B树的节点。例如下图中,将BST的根节点和两个子节点进行“两代”合并:
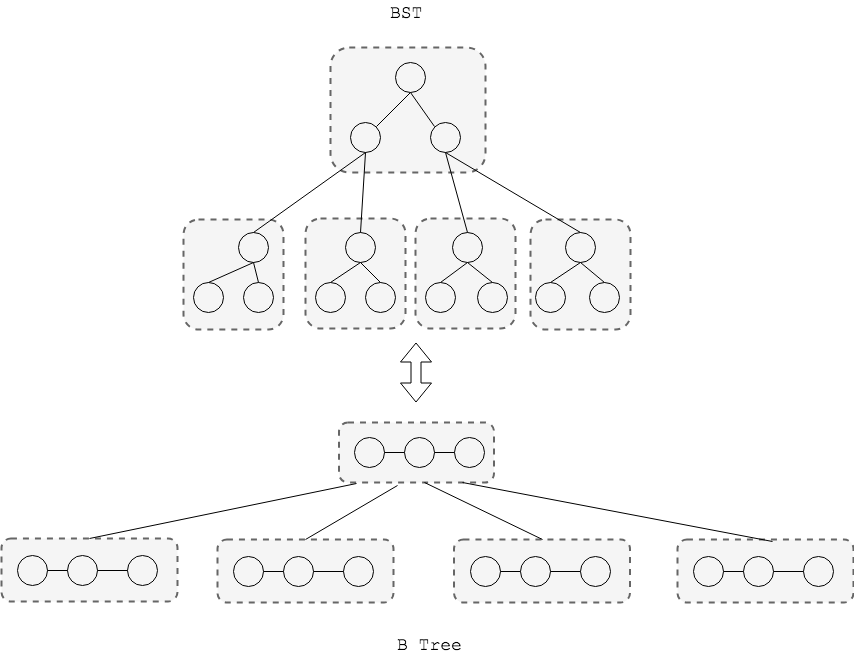
可见经过“父子”2代的合并,可以得到4路B树,其中每个节点有3个Key值,类似的:
- 每
3代合并,可得8路B树,每个节点有7个关键码 - 每
d代合并,可得到m=2^d路,每个节点有m-1个关键码
正如开篇提到的,B树适合对频繁操作的数据进行动态索引,其原因是什么呢? 如果使用前面介绍的AVL树查询,由于其具有自平衡性,其性能也应该不会太差,那为什么不用AVL树做动态索引呢?我们可以看一个具体例子:
假如我们有个1G的文件记录,我们需要查找其中的某一个,如果不允许将文件读入内存,则使用AVL树需要log(2,2^30) = 30次I/O查询操作。如果使用B树,则一次I/O可读取一组关键码,对于多数的数据库系统,通常可以支持m=256,那么回到上面问题中,使用B树一次I/O可以读入256个关键码,因此只需要查询log(256,2^30) <= 4次I/O即可。
B树的定义
任何B树都有一个固定的指标,就是它的阶次,用m表示。所谓m阶B树,即m路平衡搜索树(m>=2),它有如下性质
- 所有叶节点的深度是一致的,是一种理想平衡的搜索树
- 如果每个节点有
n个关键码(n<=m-1),则每个节点最多有n+1个分支 - 每个节点对应的分支数都不能超过
m个,所含关键码的个数不能超过m-1个(上限) - 每个节点对应的分支数不能少于 $\lceil {m/2} \rceil$ 个,其中根节点可以例外(下限)
- B树的命名规则为 $ (\lceil {m/2} \rceil, m)$树
例如下图中的B树也叫做2-3树,其m=3,也叫3阶B树,根据上面的规则,每个节点的关键码最多为m-1=2个,每个节点的分支数上限为m=3,下限为m/2=2(上取整)个
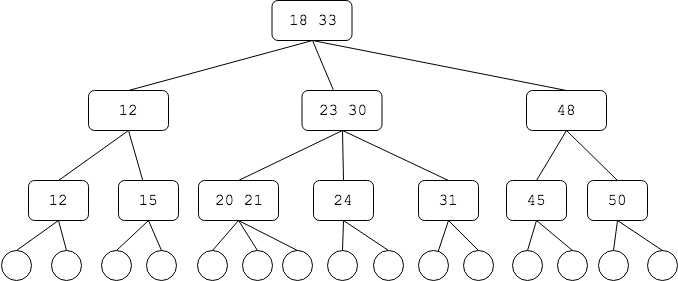
B树的表示
BTNode{
BTNode* parent;
vector<int> key; //存放key
vector<BTNode* >children; //存放子节点
}
