算法分析基础 | Algorithm Analysis Basics

Posted on 2010-01-28 | In Algorithms

递推方程

递推思想是人们常用的一种思维方式，它是一种正向的思考的过程，目的是为了找寻到某种规律，从而进行归纳和演绎，有点类似我们学过的数学归纳法。

递推最重要的是建立递推方程，所谓递推方程，指的是对于序列$a_0,a_1,…,a_n,…$简记为$\{a_n \}$，存在一个把$a_n$与某些个$a_i$联系起来的等式，叫做关于$\{a_n \}$的递推方程。举一个Fibonacci数列的例子，这个数列在算法问题中非常出名，后面会经常用到，它是一个很好的具有递推关系例子，其递推方程为：$f_n = f_{n-1} + f_{n-2}$，其中$f_0=1, f_1 = 1$。如果对该递推式进行序列求和，可以得到一个指数函数

$f_n=\frac{1}{\sqrt 5}(\frac{1+\sqrt 5}{2})^{n+1} - \frac{1}{\sqrt 5}(\frac{1- \sqrt 5}{2})^{n+1}$

这个指数函数就是$f(n)$的递推方程式，当然求解这个方程并不容易，我们下面会提到计算递推方程的几种方法。但实际上并不关心这个方程具体的解，我们只需要从渐进时间复杂度的角度分析即可。因此，我们可以认为$f(n)$的时间复杂度为$O(2^n)$。

序列求和

上面的关于Fibonacci数列的递推方程是怎么求出来的呢？它实际上是一个序列求和的结果。序列求和，是用来计算迭代问题复杂度的有效工具，由于迭代问题的不同，它们可产生的数列类型也不同，总的来说有下面几种：

算术级数，等差数列求和
- $T(n) = 1+2+…+n = \frac{n(n+1)}{2} = O(n^2)$
- $\sum_{k=1}^n a_k=\frac{n(a_1+a_n)}{2} = O(n^2)$
几何级数，等比数列求和
- $T(n) = 1+2+4+…+2^n = 2^{n+1}-1 = O(2^{n+1}) = O(2^n)$
- $\sum_{k=0}^n aq^k = \frac{a(1-q^{n+1})}{1-q}$
- $\sum_{k=0}^n aq^k = \frac{a}{1-q}(q<1) = O(a^n)$
调和级数
- $h(n) = 1+1/2+1/3 +…+ 1/n = \Theta(\log{n})$
- $\sum_{k=1}^n\frac{1}{k} ={\ln n}+{O(1)} $
对数级数
- $\log1 + \log2 + … + \log{n} = \log(n!) = \Theta(nlogn)$

递归算法的时间复杂度

递归算法的复杂度分析往往没有那么直观，常用的方法有使用递归树和主定理，我们先介绍基于递归树的分析方法。

递归树

所谓递归树就是将递归的过程用树的方式呈现出来，以归并排序为例，递归树如下图示：

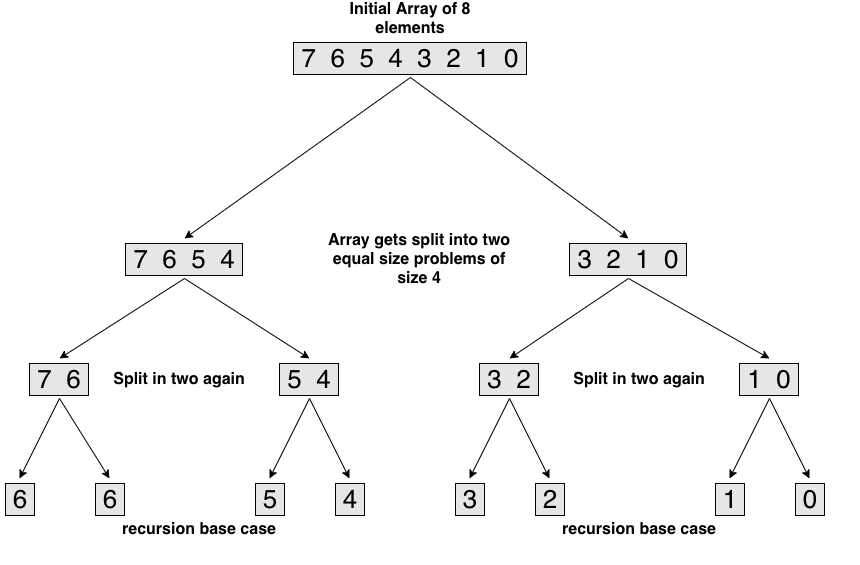
归并排序的时间复杂度公式为:

$T(n) = 2T(n/2) + n$

这个式子的递归树表示如下：

递归树是迭代计算的模型
递归树的生成过程与迭代过程一致
递归树上所有项恰好是迭代之后产生和式中的项
对递归树上的项求和就是迭代后方程的解

如果递归树上某些节点的标记为$W(m)$，则$W(m)$表示为

$W(m) = W(m_1)+...+W(m_t) + f(m) + ... + g(m)$

其中$W(m_1),…,W(m_t)$称为函数项，在递归树中为叶节点，$f(m) + … + g(m)$为根节点

主定理的证明和使用

形如下面的递推方程

$T(n) = a T(n/b) + f(n)$

其中$a$为归约后的子问题个数，$n/b$为归约后子问题规模，$f(n)$为归约过程及组合子问题的解的工作量。该类递推方程在实际引用中非常广泛，比如二分检索:$T(n) = T(n/2)+1$，二分归并排序$T(n) = 2T(n/2)n-1$，大部分算法形式包含递归。

求解上述递推方程，可分如下几种类型

若$f(n) = O(n^{\log_b{a-\epsilon}}),\epsilon > 0, \thinspace 那么 \thinspace T(n) = \Theta(n^{\log_b{a}})$
若$f(n) = \Theta(n^{\log_b{a}})，那么 \thinspace T(n) = \Theta(n^{\log_b{a}}\log{n})$
若$f(n) = \Omega(n^{\log_b{a+\epsilon}}),\epsilon > 0, \thinspace$，且对于某个常数

几种常用的递归算法时间复杂度

递推公式	时间	空间	算法
`T(n) = 2*T(n/2)+O(n)`	`O(nlogn)`	`O(logn)`	quick_sort
`T(n) = 2*T(n/2)+O(n)`	`O(nlogn)`	`O(n+logn)`	merge sort
`T(n) = T(n/2)+O(1)`	`O(logn)`	`O(logn)`	binary search
`T(n) = 2*T(n/2)+O(1)`	`O(n)`	`O(logn) ~ O(n)`	binary tree traversal
`T(n) = T(n-1) + O(1)`	`O(n^2)`	`O(n)`	quick_sort (worst case)
`T(n) = n*T(n-1)`	`O(n!)`	`O(n)`	permutation
`T(n) = T(n-1) + T(n-2) + ... + T(1)`	`O(2^n)`	`O(n)`	combination