Big O

Posted on 2010-02-03 | In Algorithms

概述

算法时间复杂度
- 针对基本运算，计算算法所运算的次数
定义基本运算
- 排序：元素之间的比较
- 检索：被检索元素x与数组元素的比较
- 整数乘法：每位数字相乘1次，m位和n位整数相乘要做mxn次位乘

代码的执行次数会因为编程语言的实现方式不同而有所差异，因此严格定义次数基本做不到

两种时间复杂度
- 最坏情况下的时间复杂度 $W(n) $
  - 输入规模为 $n $的实例所需要的最长时间
- 平均情况下的时间复杂度 $A(n) $
  - 输入规模为 $n $的实例需要时间的概率分布
$A(n) $的计算公式

设 $S $是规模为 $n $的实例集，每个实例 $I $的概率是 $PI $，算法对实例 $I $执行的基本运算次数是 $t^{I} $，则平均情况下的时间复杂度为

$A(n) = \sum_{I∈S}{P^{I}}{t^{I}}$

算法渐进分析

如果一个段程序分为几个步骤，时间复杂度分别为: $n^2 $, $100n $, $\log^{(n)}和 $1000 $，那么该程序总的时间复杂度为：

$f(n) = n^2 + 100n + \log^{(n)} + 1000$

当数据规模$n$逐步增大时，观察$f(n)$的增长趋势
当$n$增大到一定值后，计算公式中影响最大的就是$n$的幂次最高的项
常量系数（constant factor）和低幂次项（low-order term）都可以忽略

在算法复杂性分析中，$\log{n}$是以2为底的对数，以其他数值为底，算法量级不变

大O分析法

大O表示法

大O表示法：表达函数增长率的上限。令函数 $f $， $g $定义域为自然数，值域为非负实数集，如果存在正数 $c $和 $n_0 $，使得任意 $n>=n_0 $，都有 $0<=f(n)<=c*g(n) $，称 $f(n) $的渐进上界是 $g(n) $，记作 $f(n) = O(g(n)) $。表示 $f(n) $在 $O(g(n)) $的集合中，简称 $f(n) $是 $O(g(n)) $的。

看一个具体例子：假设 $f(n) = n^2 + n $, 则：

$f(n) = O(n^2) $, 取 $c=2, n_0=1 $即可;
$f(n) = O(n^3) $, 取 $c=1 $, $n_0=2 $即可

对于大O表示法有：

$f(n) $的阶小于等于 $g(n) $的阶
$c $的存在有多个，只要指出一个即可
对前面有限个 $n $值可以不满足不等式

小O表示法

函数 $f $， $g $定义域为自然数，值域为非负实数集，如果对任意正数 $c $和 $n0 $，使得任意 $n>=n0 $，都有 $0<=f(n)<c*g(n) $，记作 $f(n) = o(g(n)) $。

看一个具体例子，假设 $f(n) = n^2 + n$, 则 $f(n) = O(n^3)$。这个例子中：

$c>=1$ 显然成立, 因为$n^2+n < cn^3 (n_0=2)$
任意给定 $1>c>0$, 取 $n_0>⌈2/c⌉$ 即可,因为 $c_n>=c_0>2$ (当n>=n0),有$n^2+n < 2n^2 < cn^3$

对小O表示法，有

$f(n) $的阶小于 $g(n) $的阶
对不同的正数 $c $, $n0 $不一样， $c $越小， $n0 $越大
对前面有限个 $n $值可以不满足不等式

大Ω表示法

大Ω表示法：主要用于确认算法时间复杂度的下界。如果存在正数 $c $和 $n0 $，使得对所有 $n>=n0 $，都有 $0<= cg(n)<=f(n) $，则称 $f(n) $的渐进下界是 $g(n) $，记作 $f(n) = Ω(g(n)) $

看一具体例子，设$f(n) = n^2 + n$, 则

$f(n) = Ω(n^2)$, 取$c=1, n_0=1$ 即可
$f(n) = Ω(100n)$, 取$c=1/100$, $n_0=1$即可

对于大Ω表示法有：

$f(n) $的阶大于等于 $g(n) $的阶
$c $的存在有多个，只要指出一个即可
对前面有限个 $n $值可以不满足不等式

大Θ表示法

大θ表示法：当上，下限相同时则可以用Θ表示法。如果存在常数 $c1 $, $c2 $，以及整数 $n0 $，使得对任意的正整数 $n>=n0 $，都有： $c1g(n)<= f(n) <= c2g(n) $，或者 $f(n) = O(g(n)) $且 $f(n)=Ω(g(n)) $，则称 $f(n) = Θ(g(n)) $。

看一个具体例子，假设 $f(n) = n^2 + n$, $g(n) = 100n^2$，那么有$f(n) = Θ(g(n))$

对大Θ表示法有:

$f(n) $的大于等于 $g(n) $的阶
对前面有限个 $n $值可以满足不等式

函数渐进界定理

定理1：设 $f $和 $g $是定义域为自然数集合的函数
1. 如果 $limit n\to\infty f(n) / g(n)$ 存在，并且等于某个常数 $c>0 $，那么 $f(n) = Θ (g(n))$
2. 如果 $limit n\to\infty f(n) / g(n) = 0$ 存在，那么 $f(n) = o (g(n))$
3. 如果 $limit n\to\infty f(n) / g(n) = +\infty$ 存在，那么 $f(n) = ω (g(n))$
定理2：
定理3：设 $f $和 $g $是定义域为自然数集合的函数，若对某个其它函数 $h $，有 $f = O(h)$ 和 $g = O(h)$ ，那么 $f + g = O(h)$
函数增长率的界限通常不止一个，尽量找到最紧的
大O表示法的运算法则
- 加法规则: $f1(n) + f2(n) = O(max(f1(n),f2(n))) $
  - 顺序结构， $if $结构， $switch $结构
- 乘法规则: $f1(n) * f2(n) = O(f1(n) * f2(n)) $
  - $for，while，do-while结构 $

几类重要的渐进函数

至少指数级： $2^{n}$ , $3^{n}$ , $n!$ …
多项式级： $n$ , $n^{2}$ , $n^{1/2}$ , …
对数多项式级别： $nlogn$ , $\log^{2} n$ , $nloglogn$ , …
指数与阶乘
- $n! = o (n^{n})$
- $n! = ω (n^{n})$
- $log(n!) = Θ (nlogn)$

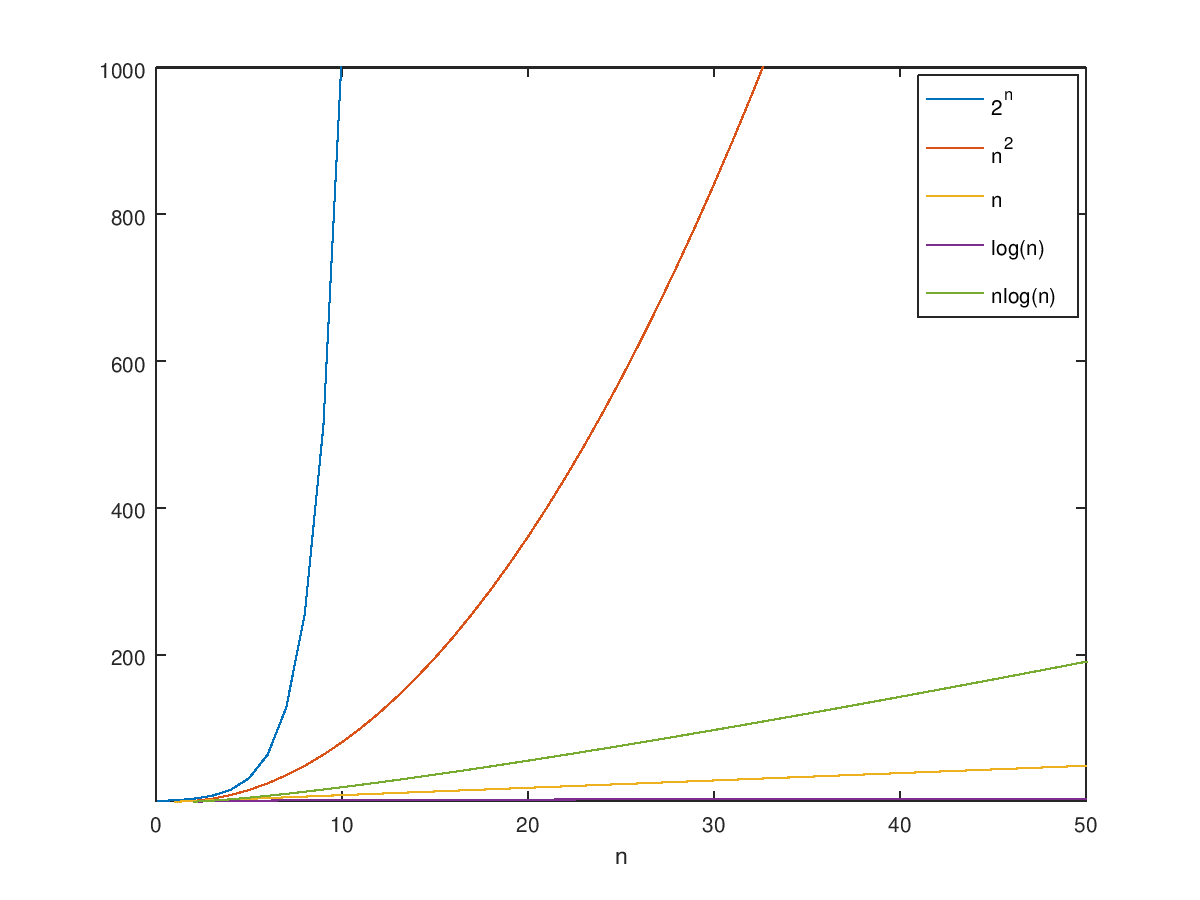
上图是上述几种函数的增长率曲线，由此不难看出： $2^{n} > n^{2} > {nlog}_{2}^{n} > n_{}^{} > \log_{2}^{n}$

为了直观的了解$O(1)$和$O(n^2)$的差别，假设数据样本的规模为2000

$O(1)$ 的算法需要$1$次运算
$O(\log{n})$ 的算法需要$7$次运算
$O(n)$ 的算法需要$2000$次运算
$O(n\log{n})$ 的算法需要$14000$次运算
$O(n2)$ 的算法需要$4000000$次运算

常用操作算法复杂度

时间复杂度	算法	最坏情况	平均情况
$O(1)$	元素之间的基本运算	$O(1)$	$O(1)$
$log(n) $	二分查找	$log(n) $	$log(n) $
$O(n) $	集合遍历，顺序查找	$O(m+n+…)$	$O(n)$
$O(nlogn) $	堆排序	$O(nlogn) $	$O(nlog(n)) $
	二分归并排序	$O(nlog(n)) $	$O(nlog(n)) $
	快速排序	$O(n^2) $	$O(nlog(n)) $
$O(n^2) $	插入排序	$O(n^2) $	$O(n^2) $
	冒泡排序	$O(n^2) $	$O(n^2) $
$O(2^n) $	斐波那契数列	$O(2^n)$	$O(2^n)$