枚举法与贪心法

Posted on 2010-02-09 | In Algorithms

枚举

枚举算法可能是日常最经常使用，也是最符合人类思考习惯的一种算法。它是基于已有知识进行答案猜测的一种问题求解策略。如求解小于N的最大素数。求解策略为

2是素数, 记为PRIM0
根据PRIM0，PRIM1, …, PRIMk, 寻找比PRIMk大的最小素数PRIMk+1
如果PRIMk+1大于N, 则PRIMk是我们需要找的素数,否则继续寻找

枚举的核心思想是猜和测，从可能的集合中一一列举各元素。这种算法要解决三个关键问题

给出解空间，建立简洁的数学模型
- 可能情况是什么
- 模型中变量数尽可能少，他们之间相互独立
减少搜索的空间
- 利用知识缩小模型中各变量的取值范围, 避免不必要的计算
- 减少代码中循环体执行次数。例如，上面例子中除2之外, 只有奇数才可能是素数, $\{ 2,2*{i+1} when {i>1} and {2 \times{i+1}}<n \}$
采用合适的搜索顺序
- 搜索空间的遍历顺序要与模型中条件表达式一致
  - 对{2,2*i+1|1<=i, 2*i+1<n}按照从小到大的顺序

百鸡百钱

鸡翁一值钱五, 鸡母一值钱三, 鸡雏三值钱一.百钱买百鸡, 问鸡翁, 鸡母, 鸡雏各几何 —— 张丘建《算经》

先分析条件：

X, Y, Z分别代表买公鸡, 母鸡和小鸡的只数
5X+3Y+Z/3=100
Z%3==0

for(int x=0; x<=100; x++){
    for(int y=0; y<=100-x; y++){
        z = 100-x-y;
        if(z%3 == 0){
            if(5*x+3*y+z/3==100){
                //x,y,z is the solution
            }
        }
    }
}

贪心法

问题求解时, 总是做出在当前看来是最好的选择，不保证全局最优，常见的贪心问题有
- 旅行推销员问题，每次选择最近城市
- 换零钱问题，每次拿面值最大的
- 图的最小生成树
- 霍夫曼编码
自顶向下计算
- 通过贪心选择, 将原问题规约为子问题
- 子问题的最优解递推到最终问题的最优解

贪心法的基本思想

基本思想
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每一子问题求解, 得到子问题的局部最优解
- 把子问题的局部最优解合并，可得到原问题的最优解，这是贪心算法的关键
  - Note:对所采用的贪心策略一定要仔细分析其是否满足 “无后效性”
算法过程
- 从问题的某一初始解出发；
- while 能朝给定总目标前进一步 do ,求出可行解的一个解元素；
- 最后，由所有解元素组合成问题的一个可行解。

局部最优与全局最优

贪心只能保证当前的选择最优，却不一定能保证最后的解是全局最优的。以换钱问题为例，假如我们有面值为20，10，5，1的4种纸币，现在想要凑36块钱，问如何选取纸币面值，使纸币数量最少？

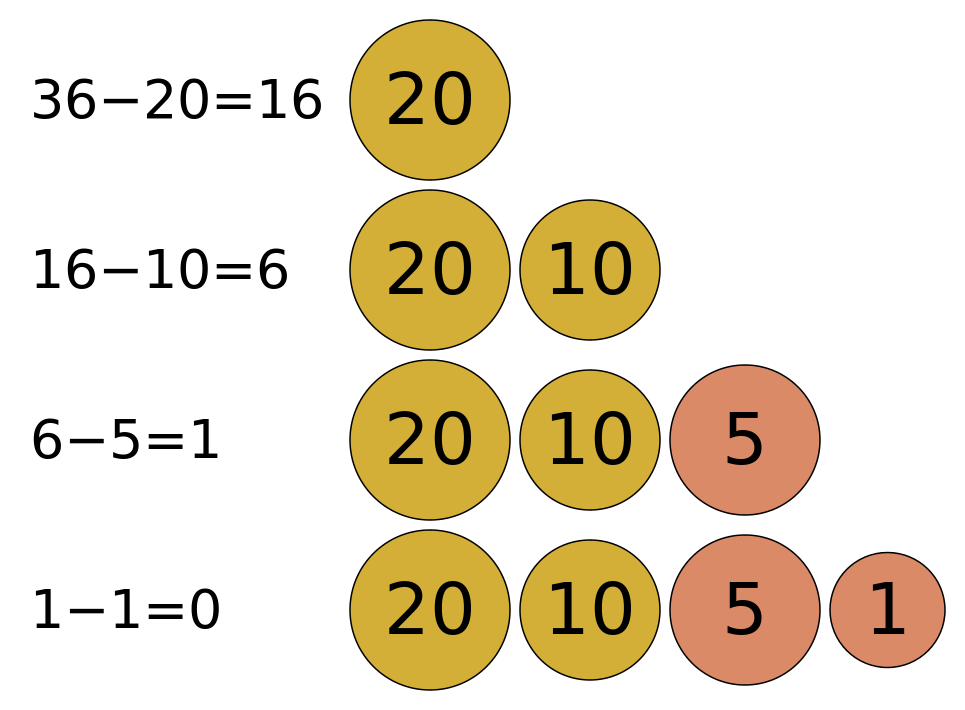
如果使用贪心法，会从面值最大的开始，向后依次选取。则结果为20，10，5，1，一共为4张。就这个问题而言，贪心法总能得到最优解。但是如果我们修改上面纸币面额为10, 9，5，1，现在要凑18，则按照贪心的思路为：18=10+5+1+1+1,需要4张纸币，而实际上我们只需要使用使用2张9块即可18=9+9。因此在这个问题上，局部最优解并不能构成全局最优解。我们再来看一个例子，下图是一课N-ary Tree，现在我们从根节点出发，想找到一条到叶子节点路径，使权值（节点的累加和）最小，该如何选择呢？

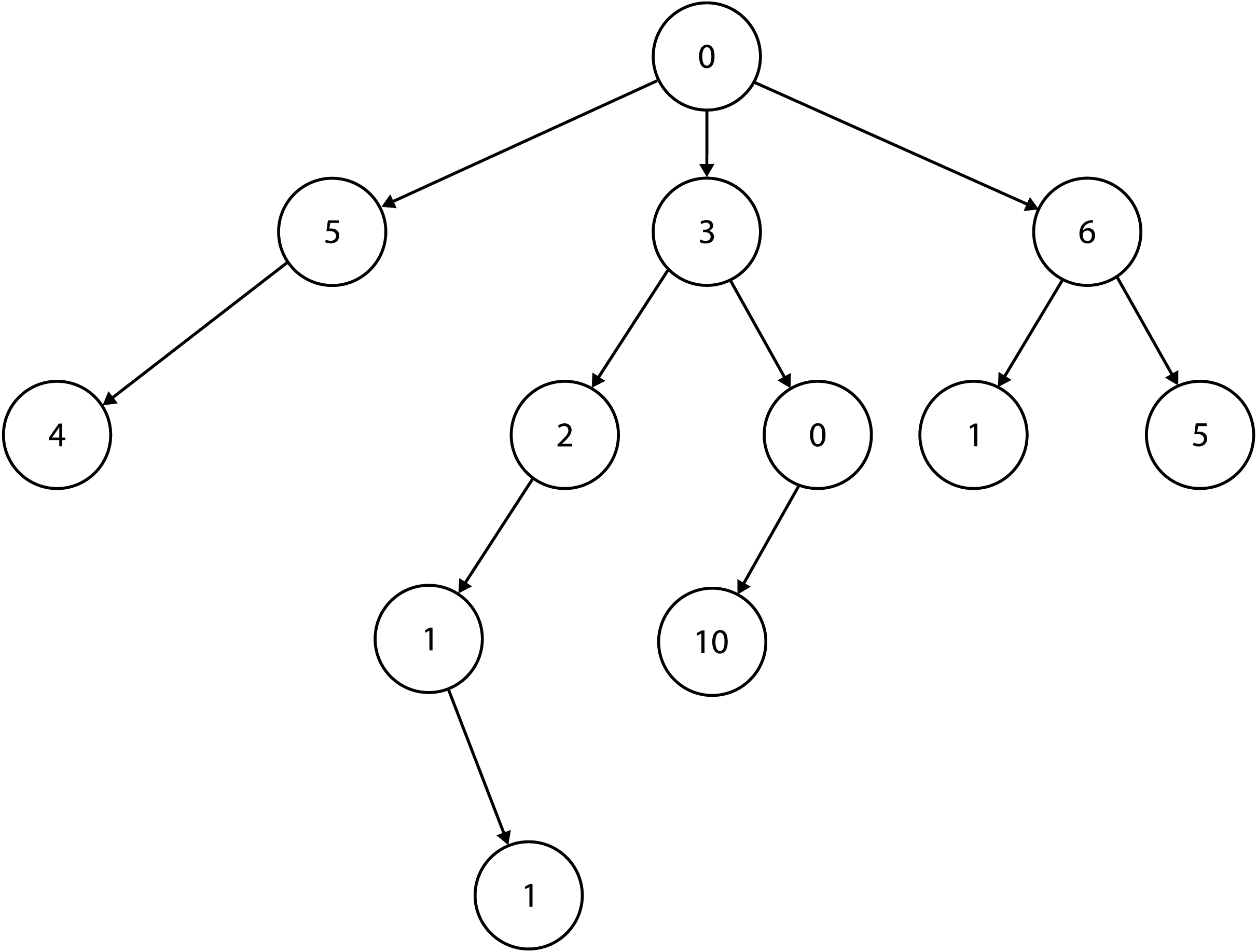
如果按照贪心的策略，那么从根节点开始每次应该选值最小的节点，结果为0 + 3 + 0 + 10 = 13，而实际上权值最短的路径为0 + 6 + 1 = 7或者0 + 3 + 2 + 1 + 1 = 7。其原因在于针对这个问题，其子问题不具备“无后效性”。即下一步的选择会影响前一步的选择，如果我们可以提前知道叶子节点是10，我们将不会选择第一条路径，也就是说10影响了我们之前的选择。那么我们该如何判断子问题是否具有“无后效性”呢？这是个非常复杂的问题，涉及很复杂的数学推导。

贪心法的应用

贪心的具体应用场景有很多，有些用到贪心的算法非常出名也非常重要，比如霍夫曼编码（Huffman Coding），最小生成树算法(Prim 和 Kruskal)，还有 Dijkstra 单源加权最短路径算法。

贪心法与动态规划

贪心法和动态规划的不同在于它对每个子问题的解决方案只做出一种当前最优的选择，不能回退。而动态规划在每一步会列出所有解的可能，并保存着些结果，然后根据这些结果做出下一步最优的选择，且具有回退功能（当某一个步结果不是最优时，回退到前一步，选择另一个解继续尝试）。

誊抄书籍

问题描述：
- 有m本书需要誊抄, 每本书的页数分别是 (p1, p2, …, pm)
- 有 k (k <= m) 个抄写员负责誊抄这些书籍
- 任务
  - 将这些书分成 k 份, 每本书必须只分给一个抄写员
  - 每个抄写员至少分到一本
  - 要求每个抄写员分到的书的编号是连续的
  - 即存在一个连续升序数列 0=b0＜b1＜b2＜…＜bk-1＜bk=m
    - 第i号抄写员得到的书稿是从bi-1+1 到第bi本书
- 问题
  - 抄写工作同时开始，抄写员抄写速度一样，先抄写完的等待，抄写完所有书籍的时间取决于被分配页数最大的抄写员完成的时间
  - 求最优的分配方式使抄书时间最少
问题的输入输出

样例输入:
2 // 2个case
9 3 //case1: 9本书，3个抄写员
100 200 300 400 500 600 700 800 900  //case1: 每本书的页数
5 4 //case2: 5 4
100 100 100 100 100 //case2: 每本书的页数
样例输出:
100 200 300 400 500/600 700/800 900 case1: 每位抄写员抄写数量通过/分割
100/100/100/100 100 case2: 每位抄写员抄写数量通过/分割

解题思路凭经验思考下，能得到两个思路：

尽量让每个人抄写的书的页数平均，这样减少等待时间
尽量减少页数最多那个抄书员所抄写的页数，平均到其它人身上

按照这两个思路继续思考，可以先求出书的总页数S = 4500, 平均到每个人身上有S/3 = 1500页，这个值可以作为阈值x，接下来可以将书按照序号累加，如果超过x就舍掉这一本，将前面的书分给一个人，后面的书分给下一个人，重新累加。依次递推可以的得到：

+ 200 + 300 + 400 + 500 = 1500; //第一个人
+ 700 = 1300; //第二个人
+ 900 = 1700; //第三个人

则最长路径为1500，可以作为抄书的最短时间。上面的思路是一种“贪心”思路，即每一步都满足一个条件，不去考虑后面的步骤，显然这种方式未必能得到最优解。同样，上面使用平均值作为阈值的思路也没有严格的数学证明，所以不一定是准确的（生活中有些凭经验去得到的结论也未必正确）。严格的做法是通过枚举来找到确定这个阈值，而从0开始枚举带来的时间消耗又太大，因此可以使用二分法来缩小搜索范围:

#下界：最多的一本书的页数（因为没人至少分配一本书）
#上界：总页数
#x = （ 上界 + 下界 ）/ 2

books = [100, 200, 300, 400, 500, 600, 700, 800, 900]  #每本书页数
k = 3  # 抄写员人数

def check(x):
    cur_pages = 0 #当前堆的总页数
    piles = 0 #总堆数
    for i in reversed(books): #反向遍历book数组
        if (cur_pages + i > x): #如果超过了x
            piles += 1 #则堆数+1
            cur_pages = i #下一堆的起始页数
        else:
            cur_pages += i #当前堆页数继续累加
    if cur_pages > 0: 
        piles += 1 #循环完，如果cur_pages > 0 ，总数+1

    return  piles<=k  #如果总堆数 > 总人数，说明x值太小了，需要增大。反之需要减少

#二分查找
l = max(books)
r = sum(books)
while(l <= r):
    mid = math.ceil((l+r)/2)
    result = check(mid)
    if(result):
        r = mid-1
    else:
        l = mid + 1

print(l, r)

经过上面计算，得到的x取值为1700。离经验值1500有些差距。上面的思路是一种“二分+判定”的贪心策略，使用二分法查找阈值x，使用堆数必须小于k个抄书员作为判定条件。这种思路是一种通用的解题策略