首页 | Home
博客 | Blog
关于 | About

二分法

Posted on | In Algorithms

二分法是实际生活中用到的最多的一种非常高效的算法，使用二分法的前提是待查找的数组是有序，其代码模板为

int bsearch(vector<int>& a, int target){
	int lo = 0;
	int hi = a.size()-1;
	while(l<=r){
		int mid = lo + (hi-lo)/2;
		if(a[mid] == target){
			return mid;
		}else if(a[mid] < target){
			lo = mid+1;
		}else{
			hi = mid-1;
		}
	}
	return -1;
}

上面实现的二分法适用于有序数组中没有重复元素的情况，但实际应用中情况往往比较复杂，数组中可能会存在大片的重复元素或者只有局部有序的情况，因此想写对二分法实际上并不容易。比如下面几种场景：

  1. 查找第一个值等于给定值的元素
  2. 查找最后一个值等于给定值的元素
  3. 查找第一个大于等于给定值的元素
  4. 查找最后一个小于等于给定值的元素

二分法的变种

对于第一个问题，如果数组中存在重复元素，则检索target到的第一个位置可能不是唯一的一个，例如下面数组：

int a[10] = { 1,3,4,5,6,8,8,8,11,18};

index:		  0 1 2 3 4 5 6 7  8  9

我们希望查找到第一个值的等于8的数据，也就是下标为5的元素。如果按照上面标准的二分法查找，则找到的8的位置位于a[7]，显然不符合我们的要求，因此，针对这种情况我们需要对上面的二分查找做一下修改。显然，一种最直观的解法是当找到8后，一路向左遍历，直到找到第一个不是8的元素，代码如下：

int a[10] = { 1,3,4,5,6,8,8,8,11,18};
int index = bsearch(a,8);
while(index>=0 && a[index] == 8){
	index--;
}

这种方式在有很多重复元素的情况下，效率并不高，比如数据为{1,8,8,8,8,8,8,8,8,9}。另一种方式是对mid-1的部分继续进行二分查找，直到找到边界点：

int bsearch(vector<int>& a, int target){
	int lo = 0;
	int hi = a.size()-1;
	while(l<=r){
		int mid = lo + (hi-lo)/2;
		if(a[mid] == target){
			//增加判断条件
			if(mid==0 || a[mid-1] != value){
				return mid;
			}else{
				hi = mid-1;
			}
		}else if(a[mid] < target){
			lo = mid+1;
		}else{
			hi = mid-1;
		}
	}
	return -1;
}

这种方式的执行效率显然高于逐个元素遍历的方式，类似的，如果想要找最后一个值等于8的元素，也只需要修改当a[mid]==target时的判断逻辑

if(a[mid] == target){
	if( mid == a.size()-1 || a[mid+1] != target){
		return mid;
	}else{
		lo = mid+1;
	}
}

接下来我们再看剩下两个问题，第三个问题是查找第一个大于等于给定值的元素，注意这里的给定值可以不在序列中，比如，数组中存储的这样一个序列：3，4，6，7，10。如果查找第一个大于等于5的元素，那就是6。这时候由于5不一定在序列中，因此不能使用a[mid]==5的条件，而需要将a[mid]==5和a[mid]>5结合起来

if(a[mid] >= target){
	if(mid==0 || a[mid-1]<target){
		return mid;
	}else{
		hi = mid-1;
	}
}else{
	lo = mid+1;
}

现在我们来看最后一个问题，查找最后一个小于等于给定值的元素。比如，数组中存储了这样一组数据：3，5，6，8，9，10。最后一个小于等于7的元素就是6。其思路和上面是一样的，这里就不展开论述了

if(a[mid] <= target){
	if(mid==a.size()-1 || a[mid]+1 > target){
		return mid;
	}else{
		lo = mid+1;
	}
}else{
	hi = mid-1;
}

这几个例子说明，在实际应用中，二分查找更适合用在“近似”查找上，在这类问题上使用二分法相比使用散列表，二叉树等效果更好。

求解一个正数的平方根

接下来我们看一个二分法的实际应用问题，该问题为求解一个正数的平方根，即实现函数sqrt(x)。这个题目有两个要求，一是我们不能使用已有的库函数，二是输入的正数包含小数。下面我们来分析下这个问题。

  1. 对于任何一个正数，如果它大于1，其平方根的取值范围为 1< s < n/2 (n>=1)。其中s表示平方根，n表示输入的正数。
  2. 如果它小于或者等于1，其平方根的取值范围为 0 < n < s <=1

综合上面两点，我们可以得出，对于任何大于0的正数n，其平方根的取值范围为0<s<1+n/2 (n>0)。 接下来我们便可以使用二分法寻找平方根，其思路为

low = 0, high = 1 + n/2
mid = low + (high-low)/2
while(true){
	s = mid*mid;
	if(s==n){
		return mid;
	}else if(s > n){
		high = mid;
	}else {
		low = mid;
	}
}

上述算法有一个问题，由于low和high的类型均为double，即s==n的情况几乎不会成立，因此我们需要对上面的二分法的判断条件做一些修改，修改方法是引入一个阈值EPSILON，这个阈值的作用是用来检查s和n的差值，如果差值小于阈值，则找到了解，否则将继续二分

const double EPSILON = 0.00001;
double sqrt(double num) {
  double l = 0;
  double r = num/2+1;
  while( l< r){
    double mid = l + (r-l)/2;
    double s = mid*mid;
    double diff = abs(s-num);
	//二分终止条件
    if(diff < EPSILON){
      return mid;
    }
    if(s < num){
      l = mid;
    }else{
      r = mid;  
    }
  }
  return -1;
}

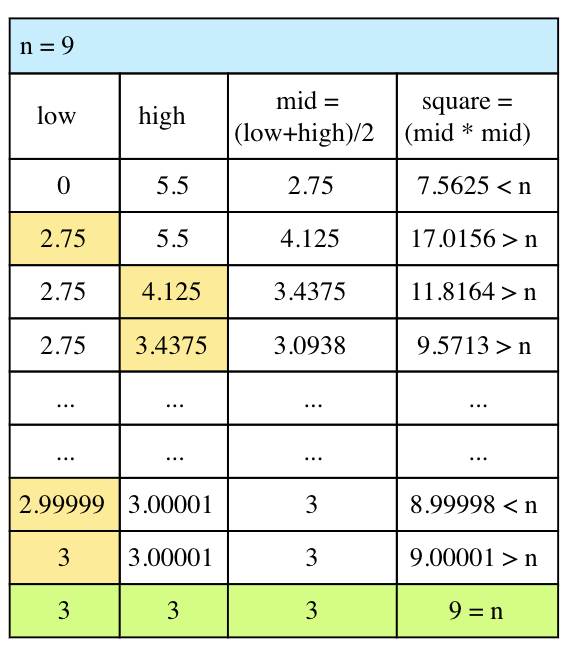
以num = 9为例，上述代码执行的过程为:

Resources

更多二分法相关问题