递归 | Recursion

Posted on 2010-02-20 | In Algorithms

递归就是编写一个特殊过程，该过程体中有一个语句用于调用过程自身。递归过程由于实现了自我嵌套的执行，可以将复杂问题拆解为若干个相同的子问题，从逐步而缩减问题规模。例如求解N的阶乘，需要先得到N-1的阶乘结果，再乘以$N$即可，而计算N-1阶乘的过程又和计算N的阶乘相同，依次类推，最终走到计算1阶乘，1阶乘结果是1，然后返回得到2阶乘的结果，返回得到3的阶乘结果，直到得到N的阶乘的结果。

理解了上面阶乘的例子后就不难想到，递归是一种自顶向下的思考方式，从问题的终局出发，向下逐层约减，这种思考方式的出现是为了利用计算机的计算能力来解决一些依靠递推很难解决的问题（比如八皇后，汉诺塔等），因为重复执行同一段程序对计算机来说几乎是无成本。但对人类来说，这种思考问题的方式通常是反直觉的，因为我们更习惯递推的思维模式，即从少到多，从具体到抽象的归纳+演绎的形式，因此递归的思维方式往往需要刻意训练才能真正掌握。

解决递归问题，重要的有三个要点：

递归式: 如何将原问题划分成子问题
递归出口: 递归终止的条件, 即最小子问题的求解,可以允许多个出口
边界函数: 问题规模变化的函数, 它保证递归的规模向出口条件靠拢

汉诺塔问题

汉诺塔问题是一个典型的自顶向下的递归问题，它原题是说：

古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求输出移动的步骤。

简单的说，汉诺塔问题的规则如下：

从A座出发，移动n个盘子到C座
A，B，C上都可以临时存放盘子
盘子有大小的区分，大盘子不能压到小盘子

接下来我们看看怎么思考这类问题，首先凭直觉，我们会做一些正向思考，也就是先会递推一些情况，比如3个盘子怎么移动，4个盘子怎么移动，分析每步怎么移动盘子，分析一会儿就容易陷入到具体的细节中而迷失方向，思路也会变得混乱，从而无法找到解法。而其背后的原因则是汉诺塔问题的规模是指数级别的，而非线性的，因此，中间细节会越来越繁琐，正向递推不容易得到结果。

如果我们换一种角度思考，忽略具体移动细节，自顶向下来思考，将问题拆成几个相同，但规模递减的子问题，则比较容易找到思路。具体来说，比如从A移动3个盘子到C，我们可以这么考虑：

将A柱上的前两个盘子移动到B柱上，这两个盘子具体怎么移动的细节不管
将A柱上的最后一个盘子移动到C柱上，移动一次，很好想
再讲B柱子上的两个盘子移动到C上，同样，这两个盘子具体怎么移动细节不管

按照上面的规律，我们可以写出算法的伪码:

//n个盘子从A到C
Hanoi(A,C,n):
    if n=1 then:
        move (A,C) //一个盘子，从A直接移到C
    else:
        Hanoi(A,B,n-1) 
        move(A,C,1)
        Hanoi(B,C,n-1)

上述代码隐含了一个条件是，B柱作为中转柱，我们怎么理解上面的代码呢？它表示的是n个盘子从起始位置移到到终点位置，并且有一个可利用的中转位置，ABC三个柱子的角色可以不断转换。因此我们可以将一个数量为n的问题，变成一个分三步的，数量为n-1的子问题，而每个子问题，又可以按照这种规则继续向下分解，直到n的数量为1，递归收敛。

这个算法的时间复杂度是怎么样的呢？我们设$n$个盘子移动的次数为$T(n)$，那么算法整体执行次数为：

\[T(n) = 2T(n-1)+1, T(1)=1\]

这个方程解出是怎么样的呢？我们可以用迭代的办法进行序列求和，得到

\[T(n) = 2^n-1\]

显然这是一个指数函数，我们假设1秒钟移动一个盘子，如果要移动64个盘子，则需要5000亿年。对这样的问题，有没有更好的算法呢？很遗憾没有，这是一个难解的问题，不存在多项式时间的解法。对于递归和递推的问题，我们后面还会做更深入的讨论。

递归的调用过程

递归调用是一个后进先出的深搜过程，分为下面几个过程：

函数调用
- 使用栈保存调用信息（参数，返回地址）
- 分配数据区（局部变量）
- 控制转移给被调函数入口
函数返回
- 保存返回信息
- 退栈，释放数据区
- 控制转移到上级函数

假设有下面的递归函数

int f(int n){
    if(n < 2){
        return n+1;
    }else{
        return f(n/2)*f(n/4);
    }
}

编译器是如何实现递归操作的呢？我们知道每次函数调用会开辟新的函数栈空间，递归调用也不例外，只不过编译器为其在栈里插入了一些辅助元素，比如递归返回的函数地址编号rd：

具体来说，其调用过程如下：

设置一工作栈当前工作记录

保存函数中出现的所有参数和局部变量
- 函数参数（值参，引用）
- 局部变量
- 返回语句标号（t+2个数值）

 typedef struct elem { // 栈数据元素类型
     int rd; // 返回语句的标号
     Datatypeofp1 p1; // 函数参数
     ...
     Datatypeofpm pm;
     Datatypeofq1 q1; // 局部变量

     Datatypeofqn qn;
 } ELEM;

设置 t+2个语句标号
- label 0 ：第一个可执行语句
- label t+1 ：设在函数体结束处
- label i (1<=i<=t) ：第i个递归返回处
增加非递归入口
- 入栈：S.push(t+1，p1, …，pm，q1，…qn
替换第 i (i = 1, …, t)个递归规则
所有递归出口处增加语句：goto label t+1;
标号为t+1的语句的格式
改写循环和嵌套中的递归
优化处理

递归树

还是上面例子的递归函数，由于其有返回值，我们可以将其改写成下面的样子：

//改写后    
void exmp(int n, int& f) {
    int u1, u2;
    if (n<2){
        f = n+1;
    }else{
        exmp((int)(n/2), u1);
        exmp((int)(n/4), u2);
        f = u1*u2;
    }
}

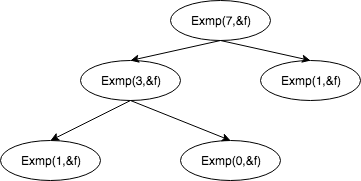
上述递归过程的递归树如图所示，可见其实际上是一个深度优先遍历（中序遍历）的过程。

递归 | Recursion

汉诺塔问题

递归的调用过程

递归树

Resources