深搜与回溯（二）

Posted on 2010-02-27 | In Algorithms

深搜的另外两个经典案例是N皇后问题和求解数独问题，由于这两个问题较为复杂，解空间的范围太大，如果不做优化，当数据规模变大时，其算法时间将会呈指数级上升。因此我们需要寻找一些优化技巧，剪枝就是其中一个常用的手段。所谓剪枝是指在深搜过程中，对不必要的路径进行裁剪，从而加快搜索速度。

N皇后问题

给你个NxN的棋盘，在棋盘上摆放N个皇后，使得这N个皇后无法相互攻击（皇后可以横竖攻击，对角线攻击），如下图中是一个8皇后问题的一个解，请给出满足N皇后条件的所有摆法

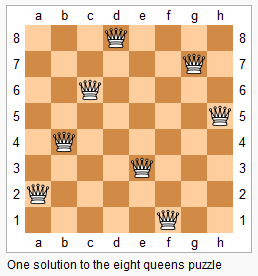
解这个问题的思路就是用DFS不断的递归+回溯，穷举所有的可能的情况。其算法步骤如下：

由于每个行或者列只能放置一个皇后，因此DFS可以按行搜索，在每行中不断尝试每个列的位置
当放置一个皇后后，在棋盘上将该位置以及其可能攻击的位置均置为不可用
搜索到不可用的位置时，直接跳过，进行剪枝操作
算法时间复杂度为指数级

//表示盘中的每个点
struct PT{
    int i;
    int j;
    bool operator<(const PT& pt) const{
        if( i<pt.i){
            return true;
        }else if(i==pt.i){
            return j<pt.j;
        }else{
            return false;
        }
    }
};
class Solution {
    //放置一个皇后，更新棋盘状态
    set<PT> place(int i, int j, vector<vector<char>>& board){
        set<PT> us;
        //竖向
        for(int k=0;k<board.size();k++){
            if(board[k][j] !='.' && board[k][j] != 'Q'){
                board[k][j] = '.';
                us.insert({k,j});
            }
        }
        //横向
        for(int k=0;k<board.size();k++){
            if(board[i][k] != '.' && board[i][k] != 'Q'){
                board[i][k]= '.';
                us.insert({i,k});
            }
            
        }
        //对角线1
        for(int p=i, q=j; p>=0 && q>=0 ; p--,q--){
            if(board[p][q] != '.' && board[p][q] != 'Q'){
                board[p][q] = '.';
                us.insert({p,q});
            }
        }
        for(int p=i,q=j; p<board.size()&&q<board.size();p++,q++){
            if(board[p][q] != '.' && board[p][q] != 'Q'){
                board[p][q] = '.';
                us.insert({p,q});
            }
        }
        //对角线2
        for(int p=i,q=j; p>=0 && q<board.size();p--,q++){
            if(board[p][q] != '.' && board[p][q] != 'Q'){
                board[p][q] = '.';
                us.insert({p,q});
            }
        }
        for(int p=i,q=j; p<board.size() && q>=0;p++,q--){
            if(board[p][q] != '.' && board[p][q] != 'Q'){
                board[p][q] = '.';
                us.insert({p,q});
            }
        }
        board[i][j] = 'Q';
        us.insert({i,j});
        return us;
    }
    //回溯棋子后复原棋盘状态
    void unplace(set<PT>& us, vector<vector<char>>& board){
        for(auto itor = us.begin(); itor!=us.end(); itor++){
            auto p = *itor;
            board[p.i][p.j] = 'x';
        }
    }
    //深搜
    void dfs(int n, int row, int sz, vector<vector<char>>& board, vector<vector<string>>& result){
        if(n == 0){
            vector<string> v;
            for(auto vec:board){
                string tmp="";
                for(auto c:vec){
                    tmp+=c;
                }
                v.push_back(tmp);
            }
            result.push_back(v);
            return;
        }
        //按行搜索，尝试列位置，j代表列
        for(int j=0;j<sz && row<sz;j++){
            if(board[row][j] == 'x'){ //剪枝
                //choose
                auto pts = place(row, j, board);
                cout<<"set state: "<<endl;
                log(board);
                n-=1;
                //深搜
                dfs(n,row+1,sz,board,result);
                //backtrack
                n+=1;
                unplace(pts, board);
                cout<<"reset state: "<<endl;
                log(board);

            }
        }
    }
    //打印棋盘状态
   void log(vector<vector<char>>& board){
        for(auto vec:board){
            for(auto c:vec){
                cout<<c<<" ";
            }
            cout<<endl;
        }
        cout<<"--------"<<endl;
    }
    
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<char>> board(n,vector<char>(n,'x'));
        vector<vector<string>> ans;
        dfs(n,0,n,board,ans);
        return ans;
    }
};

Sudoku问题

我们再来看一道数独问题，和N皇后问题一样，求解数独问题也是一个利用暴力搜索的典型应用。

将数字1到9,填入9x9矩阵中的小方格，使得矩阵中的每行，每列，每个3x3的小格子内，9个数字都会出现”。

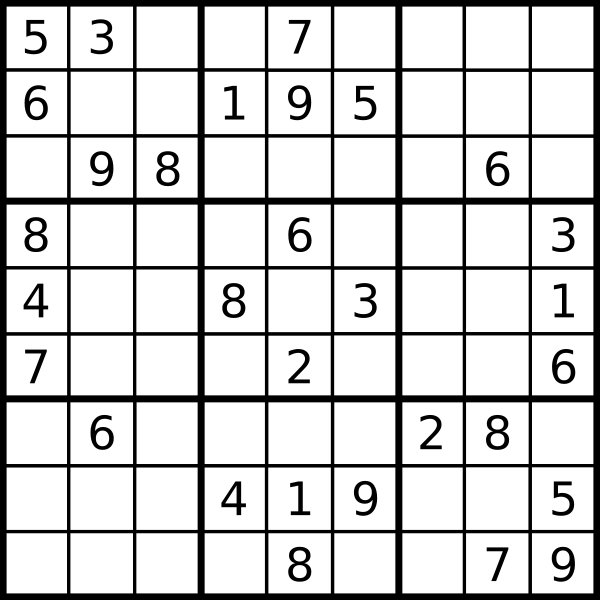
解数独问题的思路为在每个空位依次尝试从1-9的每个值，每放置一个后进行DFS搜索，如果所有空位都能填满则返回一组解，如果有空位不满足条件，则进行回朔，重置状态后再换另一个数字尝试DFS，知道尝试完所有的空位。

vector<vector<bool>> row_state(9,vector<bool>(10,false)); //标志位，存放每行1-9出现的标志，1为放置，0为未放置
vector<vector<bool>> col_state(9,vector<bool>(10,false)); //标志位，存放每列1-9出现的标志，1为放置，0为未放置
vector<vector<bool>> block_state(9,vector<bool>(10,false)); //标志位，存放每个小块1-9出现的标志，1为放置，0为未放置

//根据x，y计算对应的block index
int blockIndex(int r, int c){
  return r/3 * 3 + c/3;
}

//每放一个棋子需要更新 state
void set_state(int r, int c, int num, bool value){
  int index = blockIndex(r,c);
  col_state[c][num] = value;
  row_state[r][num] = value;
  block_state[index][num] = value;
}
//当前位置是否已经被放置过
bool is_valid(int r, int c , int num){
  int index = blockIndex(r,c);
  if(!row_state[r][num] && 
     !col_state[c][num] && 
     !block_state[index][num]){
    return true;
  }
  return false;
}
bool dfs(int index, vector<pair<int,int>>& blanks, vector<vector<char>>& board){
  
  if(index >= blanks.size()){
    return true;
  }
  int row = blanks[index].first;
  int col = blanks[index].second;
  
  //每个空白位置尝试1-9
  for(int n=1;n<=9;n++){  
      if(!is_valid(row,col,n)){
        continue;
      }
      //choose
      set_state(row,col,n,true);
      //dfs
      if(dfs(index+1,blanks,board)){
        //剪枝
        return true;
      }else{
        //backtracking  
        set_state(row,col,n,false);
      }
  }
  return false;
}

bool sudokuSolve( const vector<vector<char>>& input ) {
  
  vector<vector<char>> board = input;
  vector<pair<int,int>> blanks;
  
  for(int i=0; i<board.size(); i++){
    for(int j=0;j<board.size();j++){
      char c = board[i][j];
      int num = c-'0';
      if(c == '.'){
        blanks.push_back({i,j});
      }else{
        //modify the board
        set_state(i,j,num,true);
      }
    } 
  }
  //深搜
  return dfs(0,blanks,board);
}

深搜与回溯（二）

N皇后问题

Sudoku问题

Resources

关于DFS的更多问题