分而治之 | Divide and Conquer
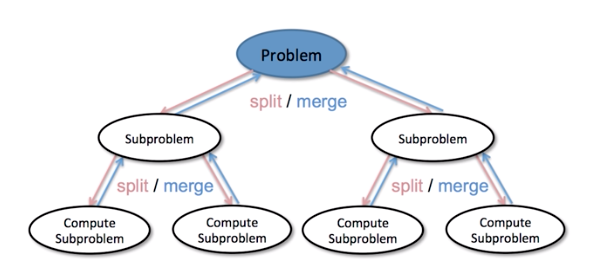
分治法的设计思想
分治法顾名思义,其思想为”分而治之”,是指将一个大问题分解为若干个(通常是两个)规模大体相当的子问题,由子问题的解得出原问题的解。分治法要求子问题具备以下几个特征:
- 子问题与原问题性质完全一样
- 子问题之间彼此独立的求解
- 递归停止时子问题可直接求解
上述三点中的前两点尤其重要,子问题的与原问题的性质相同决定了我们可以使用递归的方式来求解子问题,可以大大的简化计算步骤。对于第二点则更为重要,如果子问题之间不能满足独立求解(彼此有耦合),那么该问题将不适合用分治法求解,例如动态规划同样是将原问题划分为子问题,但是子问题的求解往往依赖其它子问题的状态,彼此之间并不独立。正是由于其子问题的独立性,我们往往可以是用并行计算来同时处理多个子问题,例如对较小规模的子问题可以进行多线程处理,对规模较大的子问题,可使用目前流行的分布式计算MapReduce。
分治法的算法思路如下:
- 将原问题划分为或者归结为规模较小的子问题
- 迭代或者递归求解每个子问题
- 将子问题的解综合得到原问题的解
根据前面介绍的子问题的特征,我们可以总结出一套分治法的代码模板:
def divide_conquer(problem, param1, param2, ...):
#recursion terminator
if problem is None:
print result
return
# process data
data = prepare_data(problem)
subproblems = split_problem(problem,data)
# divide
subResult1 = self.divide_conquer(subproblems[0], p1, ...)
subResult1 = self.divide_conquer(subproblems[1], p1, ...)
subResult1 = self.divide_conquer(subproblems[2], p1, ...)
...
# conquer, process and generate the final result
result = combineResult(subResult1,subResult2, subResult3,...)
寻找无序数组的中位数
我们的第一个例子是求解无序数组的中位数问题,中位数的定义为
二分搜索与归并排序
在前面文章中,我们曾介绍过二分搜索,当时算法是使用迭代的形式给出的,我们可以将二分搜索以分治法的思想进行递归改写,通过x与中位数比较,将原问题归结为规模减半的子问题,如果x小于中位数,则子问题由小于x的数构成,否则子问题由大于x的数构成。
binarySearch(a[],l,r,t)->int:
if r==l:
return a[l] == t ? l:0
mid = (r+l)/2;
if a[mid] == t:
return mid
else if a[mid] < t:
return binarySearch(a,mid+1,r,t)
else
return binarySearch(a,l,mid-1,r,t)
接下来我们来分析下二分法的时间复杂度,我们以数组[1,2,3,4,5]为例,最坏情况下的搜索次数为多少呢?加入我们要搜索1.5显然它不再数组中,我们需要比较3次才能得出这个结果,推而广之,如果一个数组的个数为$n$,那么二分法最坏情况下的时间复杂度为:
可以解出,
\[W(n) = \lfloor \log{n} \rfloor + 1\]归并排序是另一个很好的分治+二分的例子,其排序思路为:
- 原问题归结为规模为$n/2$的两个子问题
- 对子问题进行继续怀芬,归结为规模为$n/4$的子问题,以此类推,当子问题规模为1时,划分结束。
- 从规模1到$n/2$,陆续归并被排好序的两个子数组,每归并一次,数组规模扩大一倍
算法伪码如下:
MergeSort(A,p,r)
输入: 数组A[p...r]
输出: 排序后的数组A
if p<r
then q<-⌊(p+r)/2⌋ //二分
MergeSort(A,p,q) //子问题1
MergeSort(A,q+1,r) //子问题2
Merge(A,p,q,r) //合并解
我们使用递归树来分析其时间复杂度
- 对递归树的每一层 $j=0,1,2…,log_2{n}$,有$2^j$个节点,每个节点代表一个需要继续递归的子数组
- 对第$j$层,和并需要的时间为$6n$(可通过对merge函数的分析得到)
- 归并排序一共需要执行的次数为:$6n*(\log{n}+1) = 6n\log{n} + {6n}$
