加权最短路径 | Weighted Shortest Paths

Dijkstra算法

路径的权值在某些场合下是非常重要的，比如两地间飞机的票价，两个网络节点间数据传输的延迟等等。DFS和BFS在搜索两个节点路径时不会考虑边的权值问题，如果加入权值，那么两点间权值最小的路径不一定是BFS得到的最短路径，如下图中求$\{a,f\}$两点间的BFS的结果为$\{a,e,f\}$，cost为9，而cost最少的路径为$\{a,d,g,h,f\}$，其值为6

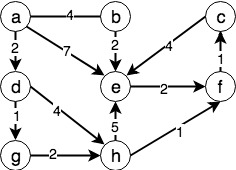
Dijkstra算法研究的是单源最短路径(single-source shortest paths)问题，即给定带权图 G = <V,E>，其中每条边 $(v_i，v_j)$ 上的权 $W[v_i，v_j]$ 是一个非负实数。计算从任给的一个源点s到所有其他各结点的最短路径。

Dijkstra算法的基本思想是使用贪心法维护一个数据结构，记录当前两点间的最短路径，然后不断更新路径值，直到找到最终解。

function dijkstra(v1,v2):
    //初始化所有节点的cost值
    for v in all vertexes{
        v.cost = maximum
    }
    v1.cost = 0
    //创建一个最小堆保存顶点，优先级最低的顶点在堆顶部
    priority_queue pq(v1.cost);

    while !(pq.empty()){
        v = pq.front(); //弹出优先级最低的vertex
        v.status = visited
        if v == v2:
            //找到v2
            break;
        //遍历v的每一个未被访问的相邻节点
         for n : v.unvisited_neighbors:
            //计算到达n的cost
            cost := v.cost + weight of edge(v,n)
            if cost < n.cost:
                n.cost = cost
                //记录前驱节点
                n.prev = v
                pq.push( n.cost )
    }
    //使用v2的前驱节点，重建到v1的路径

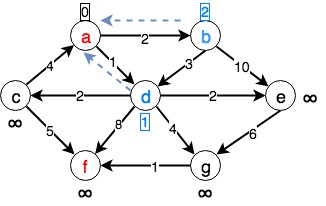
上述是Dijkstra算法的伪码，我们通过下面一个例子看看它是如何工作的。如下图所示，假设我们要求从$\{a,f\}$的权值最短路径。

1. 初始化各节点的cost为无穷大，令a的cost为0，放入优先级队列pq

2. 从pq中取出顶部节点，访问它的相邻节点b,d，计算到达b,d的cost，分别为2,1，由于2,1均小于b,d原来的cost(无穷大)，因此将b,d的cost更新，放入到优先队列，第一次选择（循环）结束，此时队列中的顶点为pqueue = {d:1,b:2}

3. 重复步骤2，pq顶部的节点为d,找到d相邻的节点c,f,g,e分别计算各自的权重为3,9,5,3，均小于各自cost值（无穷大），因此c,f,g,e入队，第二次循环结束，此时队列中的顶点为pqueue = {b:2,c:3,e:3,g:5,f:9}

4. 重复步骤2，pq顶部的节点为b，找到b相邻的节点d,e，由于d在上一步中已经被访问了，于是略过d，计算b到e的cost为2+10=12，大于e在上一步得到的cost3，因此直接返回。第三次循环结束，此时队列中的顶点为pqueue = {c:3,e:3,g:5,f:9}

5. 重复步骤2，pq顶部的节点为c,找到d相邻的节点f，计算到达f的权重为8，小于队列中的9，说明该条路径优于第三步产生的路径，于是更新f的cost为8，更新f的前驱节点为c。第四次循环结束，此时队列中的顶点为pqueue = {e:3,g:5,f:8}

6. 重复步骤2，pq顶部的节点为e，找到e相邻的节点g，计算e到g的cost为3+6=9，大于g在之前得到的cost5，因此直接返回。第五次循环结束，此时队列中的顶点为pqueue = {g:5,f:8}

7. 重复步骤2，pq顶部的节点为g，找到g相邻的节点f，计算g到f的cost为5+1=6，小于f在之前得到的cost8，说明从g到达f这条路径更优，于是更新f的cost为6，更新f的前驱节点为g，此次循环结束，此时队列中的顶点为pqueue = {f:8}

8. 重复步骤2，发现已经到达节点f因此整个循环结束。然后从f开始根据前驱节点依次回溯，得到路径f<-g<-d<-a，为权值最优路径。

从上面的求解过程可以发现Dijkstra算法实际上是一种贪心算法，即每一步都找当前最优解（最小堆堆顶元素)。对于贪心法，它实际上是动态规划算法的特例，因此要求每一步的重复子结构解具有无后效性。对应到Dijkstra算法，要求路径的权值不能为负数。因为如果出现负数，当前的最优选择在后面不一定是最优。

• Dijkstra算法时间复杂度

对于稀疏图，Dijkstra算法使用最小堆实现效率较高：

1. 初始化: $O(v)$
2. While循环： $O(v)$
   • remove vertex from pq: $O(\log{V})$
   • potentially perform E updates on cost/previous
   • update costs in pq: $O(\log{V})$
3. 路径重建： $O(E)$
4. 总的时间复杂度为: $O(V\log{V}+E\log{V}) = O(E\log{V})$ (如果图是连通的，有$V=O(E)$)

A* 算法

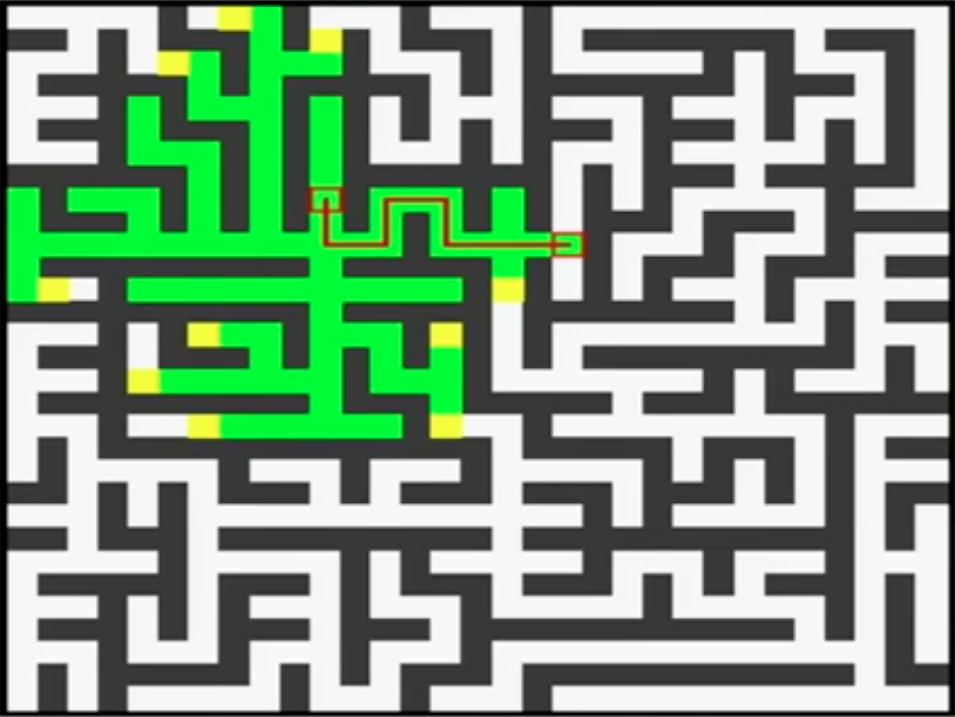
A*是另一种寻找权值最优路径的方法，它是对Dijkstra算法的一种改进。Dijkstra虽然可以找到最短路径，但是BFS的寻找过程却不是最高效的，如下图所示

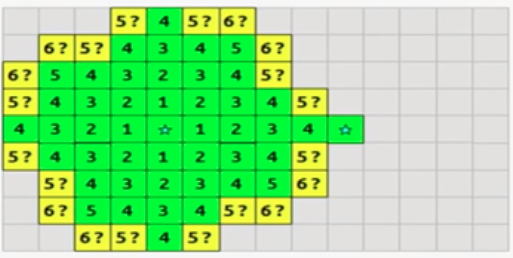
假设我们要从中心点走到最右边的点，由于从中心扩散出去的每个点权值都相同，Dijkstra算法会在四个方向上不断尝试每个扩散出去的点，显然，这种搜法包含大量的无效搜索。仔细思考不难发现，其原因在于Dijkstra算法基于贪心策略每次只能确定当前最短距离，而不知道哪个方向才能逼近终点，如下图中，Dijkstra每次只能确定由a节点确定b节点，而对于终点c在哪则毫无所知，没有任何信息：

针对这个问题，A*算法改进了Dijkstra，引入了一个Heuristic的估计函数来来确定节点的扩散方向，使其可以沿着终点方向逼近，如下图所示

在引入了一个Heuristic函数后，我们相当于知道了一些额外的信息，这些信息可以帮助我们减少不必要的搜索。假设我们想要找从a到c的权值最小路径，对于任何中间节点b，我们要计算两个值

1. 从a到b确定的权值(同Dijkstra)
2. 从b到c的估计值（estimated cost）

A*的整体算法框架同Dijkstra相同，只需要将最小堆中存放的cost改为cost(n) + H(n,target)即可

v1.cost = H(v1,v2)
priority_queue pq(v1);
//...
pq.push( n.cost + H(n,v2) )

A* 算法的难点在于如何找到合适的Heuristic函数，不同的搜索场景，使用的Heuristic也不相同，例如下面场景，我们希望从a走到c:

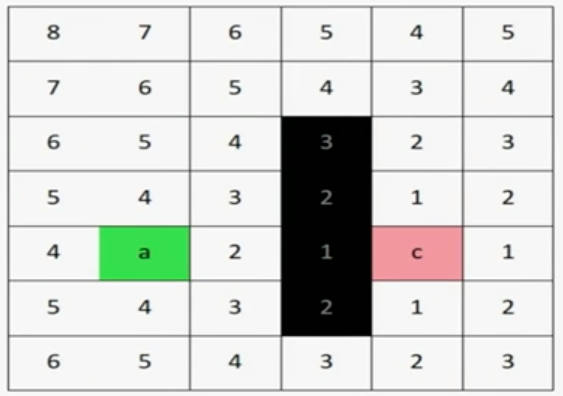
此时可以将Heuristic函数定义为:H(p1,p2) = abs(p1.x-p2.x) + abs(p1.-p2.y)，则根据这个公式计算出的cost值如上图中每个格子所示，可以看到，从a点扩散出去的节点不再是等cost的，而是越偏向c点，cost的值越低。

关于Heuristic函数有一点需要特别注意的是，对终点cost的估计不能over estimate，也就是估计出来的值比实际值要大很多，这样会导致真实的最短路径一直被压在最小堆中，产生不必要的冗余计算。虽然Heuristic函数不可以over estimate，但是却可以under estimate。

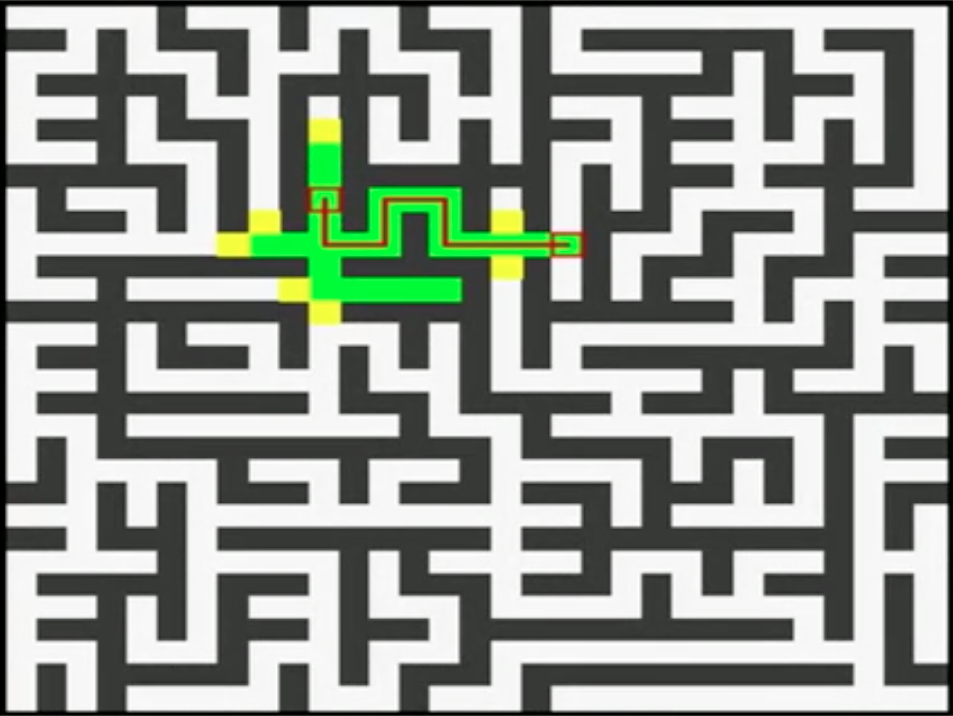
最后我们以一个迷宫的例子来直观的比较一下Dijkstra和A*算法的效率，如下图所示，左边为Dijkstra算法结果，需要走103步，右边是A*算法，只需要25步（图中格子之间路径的cost均为1）