动态规划 | Dynamic Programming
概述
在介绍动态规划之前,我们先来想一下最符合人类思维习惯的蛮力算法。所谓蛮力算法是指穷举所有可能的解法,或者搜索解空间中的所有分支,然后在有解中寻找符合条件的解。以搜索为例,蛮力算法的一个问题在于每两次搜索之间的关系是相互独立的,相互独立意味前一步搜索所产生的信息无法被后一步所利用,这会导致这些信息的浪费,而且在某些情况下,当前这次者搜索还会重新走一遍上次“老路”来获得前一步已经得到的这些信息,这显然这是一个非常低效的策略。
而所谓的动态规划,是一种多阶段的决策过程,它将每个阶段得到的结果不断的积累起来,在后面阶段的决策中充分利用这些已经得到的结果进行决策,从而避免错误的选择,进而提高整个算法的效率。
动态规划最早是由Richard Bellman在1950年提出,起初是用来求解数学中的求解最优化问题,后来这种思想也被迁移到了计算机科学中,如果一个问题具有最优子结构(即一个问题可被分解成多个相同,但规模更小的子问题,并且可以递归的找到这些问题的最优解),则可以使用动态规划算法求解。
接下来我们先给出求解DP问题的一般方法,然后分析一系列动态规划的经典问题,包括:
- 对穷举或者搜索问题的优化
- 求解最优化问题
求解DP问题的一般方法
- 将原问题分解为子问题
- 把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题解决,原问题即解决
- 子问题的解可以缓存,所以每个子问题只需要求解一次
- 确定状态
- 将和子问题相关的各个变量的一组取值,称之为一个
状态,一个状态对应于一个或多个子问题,所谓某个状态下的值,就是这个状态所对应的子问题的解 - 所有
状态的集合,构成问题的状态空间。状态空间的大小解解决问题的时间复杂度直接相关。整个问题的时间复杂度是状态数目乘以每个状态所需要的时间 - 经常碰到的情况是,K个整型变量能够成一个状态。如果这个K个整型变量的取值范围分别是
N1,N2,...,Nk,那么,我们就可以用一个K维数组array[N1][N2]...[Nk]来存储各个状态的值。这个值未必是一个整数或浮点数,也可以是一个复杂的数据结构
- 将和子问题相关的各个变量的一组取值,称之为一个
- 确定一些初始状态(边界状态)的值
- 确定状态转移方程
- 找到不同状态之间如何迁移-即如何从一个或多个值已知的状态,求出另一个状态的值。状态的迁移可以用递推公式表示,递推公式也可被称作状态转移方程
- 递推公式可以从前往后推导,也可以从后向前推导
- 当选取的状态,难以进行递推时(分解出的子问题和原问题形式不一样,或不具有无后效性),考虑将状态增加限制条件后分类细化,即增加维度,然后在新的状态上尝试递推
- 找到不同状态之间如何迁移-即如何从一个或多个值已知的状态,求出另一个状态的值。状态的迁移可以用递推公式表示,递推公式也可被称作状态转移方程
一维动态规划问题
由于动态规划的问题比较复杂也比较抽象,我们至少需要用两篇文章才能彻底搞清楚解DP问题的思路,我们先从一维状态的问题入手,慢慢过渡到二维以及三维的问题。本文以及下一篇文章中所使用的例子均是非常经典的动态规划问题,举些例子的目的是为了观察DP问题的形式以及解DP问题的一般规律。DP之所以难是因为它的解法通常不直观,状态的定义通常不容易想到,进而设计不出正确的状态转移方程。想要熟练的解DP问题没有什么特别好的办法,只有多练,然后总结,然后再练,如此反复的进行刻意练习。
斐波那契数列
给定数字n,和斐波那契公式,求解第n个斐波那契数
- 使用递归
不难想到,这个问题使用递归的方法接比较容易,因为每一步的计算过程都是相同的,我们只需要让计算机不断重复这个过程即可:
def fib1(n):
if n==0 or n==1:
return n
else:
return fib1(n-1)+fib1(n-2)
我们来分析一下,当 n=5时,fib(5)的递归计算过程如下:
fib(5)
= fib(4) + fib(3)
= (fib(3) + fib(2)) + (fib(2) + fib(1))
= ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
= (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
可以看到,上面的递归过程存在大量的重复计算,例如fib(3),fib(2),fib(1),fib(0),由于这些计算结果没有缓存,因此每次计算一个新的fib值时,这几个数都要重新计算。我们来分析一下使用递归解法的时间复杂度,我们先看看斐波那契数列的递推式$f_n = f_{n-1} + f_{n-2}$,其中$f_0=1, f_1 = 1$。可以对该数列求和得到
显然这是一个指数函数。接下来我们分析算法的时间复杂度,不难看出,时间复杂度的递推式为:$T(n) = T(n-1) + T(n-2) + 1 \thinspace (n>1)$,同样为一个斐波那契数列,可以得出$T(n)$正比于斐波那契的递推式$f(n)$,即
\[T(n) = 2 * fib(n+1)-1 = O(fib(n+1)) = O(\Phi^n) = O(2^n)\]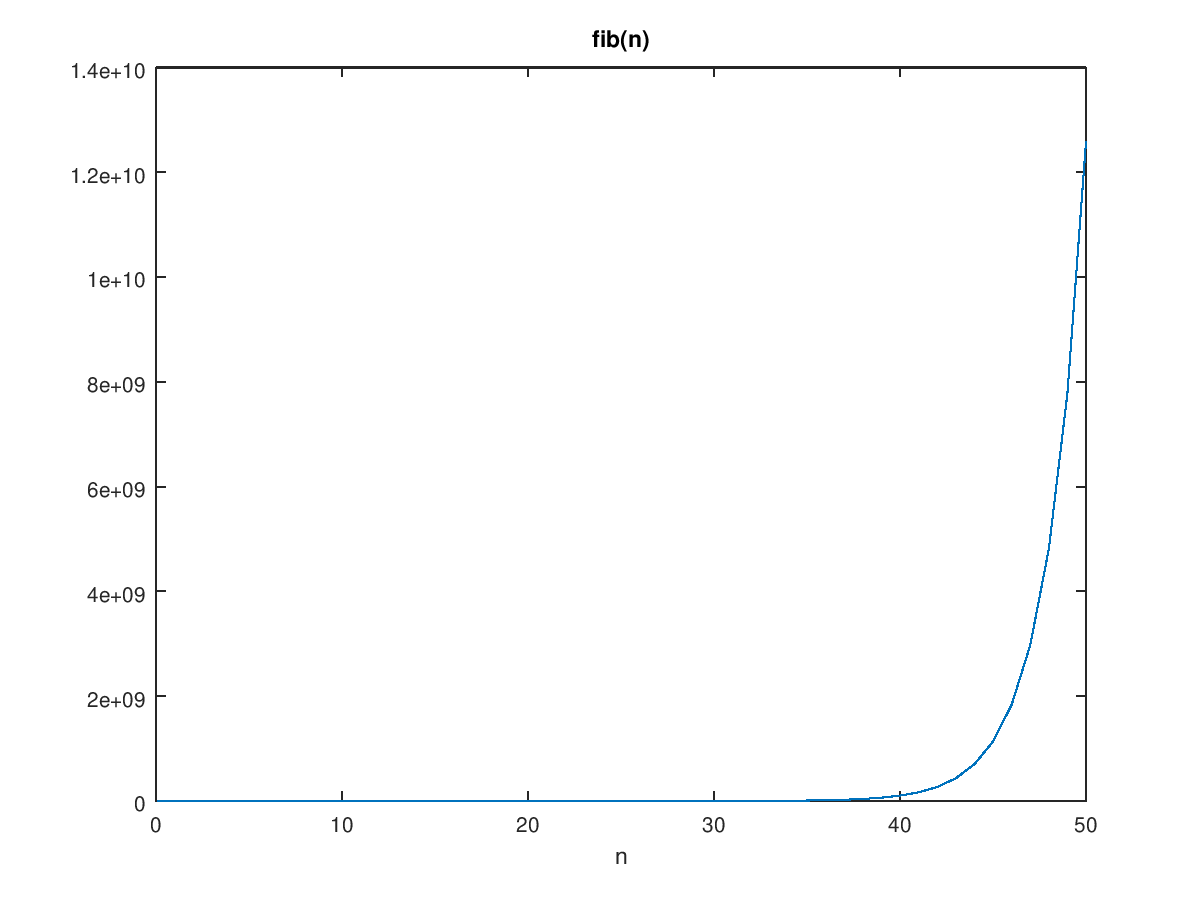
显然它的时间复杂度递推式也是只呈指数级增长的,这类量级的算法在实际应用中显然是不适用的,实际测试可发现当n>60时,算法运行时间将变成秒级。
- 使用记忆化递归
可以看到,使用简单的递归的一个比较大的问题是存在大量的重复运算,因此一个简单的优化是对中间计算的结果进行缓存(memoization),整个计算过程还是递归向下的
#Recursion + Memoization
def fib2(n,memo):
if n in memo:
return memo[n]
else:
if n==0 or n==1:
return n
else:
v = fib2(n-1,memo)+fib2(n-2,memo)
memo[n] = v
return v
引入缓存后,计算得到效率大大提升。我们再来分析下时间复杂度,读缓存需要$O(1)$的时间,fib序列中的每一项只计算一次,共需要$O(n)$时间,因此最后时间复杂度变成了:
\[T(n) = O(n)+O(1) = O(n)\]- 转为迭代
根据前面的4条结论,记忆化递归可以转为使用迭代的方式进行求解:
#DP
def fib3(n):
fib ={}
fib[0] = 0
fib[1] = 1
for i in range(2,n+1):
fib[i] = fib[i-1]+fib[i-2]
return fib[n]
改为迭代算法后,时间复杂度依然为$O(n)$,空间复杂度仅为$O(n)$。这种计算方式和使用递归+缓存的方式基本一致,不同的是计算方向,将递归这种自顶而下的计算方式改为了自底向上的迭代。也可以将其理解为是一种拓扑序列结构,项与项之间有依赖关系:

两点间路径(Unique Paths)
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).How many possible unique paths are there?
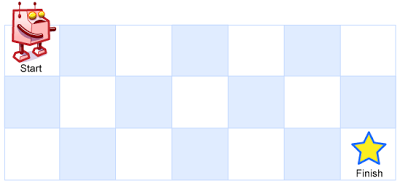
上面问题是说,在一个m x n的棋盘上(n行,m列),在每一个格子上只能向右或者向下两种走法,那么从start(左上角)走到finish(右下角)有几种不同的走法?如上面例子中,到达end的路径有三条,分别是:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
- 蛮力算法
首先想到的是还是使用蛮力算法,类似走迷宫,搜索可抵达边界的每条路径,当搜走到右下角时,记作一次发现,将每次发现的次数计起来即可得到最终解。由之前介绍的深搜思路,机器人每到一个位置时都有两种走法,向右或者向下,因此到达终点的路径数为从右边走和从下边走结果的总和。
/*
Solution: DFS + backtracking
Time Complexity: O(2^n)
Space Complexity: O(1)
*/
class Solution {
public:
/*
i,j: 当前位置
w,h: 迷宫宽高
*/
int dfs(int i, int j, int w, int h){
if(i<0||i>=h || j<0||j>=w){
return 0;
}
if(i==h-1 && j==w-1){
return 1;
}
int cd = dfs(i+1,j,w,h,result);
int cr = dfs(i,j+1,w,h,result);
return cd + cr;
}
int uniquePaths(int m, int n) {
return dfs(0,0,m,n,num);
}
};
上述解法的确能够穷举出所有到达右下角的路径,然而效率确非常低。我们可以来分析一下上述解法的时间复杂度,由于每一个格子(非边界的情况)都有两种选择,向下或者向右,因此其时间复杂度和上面计算斐波那契数列一样,为几何级数O(2^n)。以3x3的棋盘为例,递归树如下:
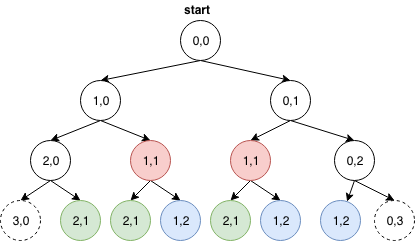
不难看出,上面的递归过程存在大量的重复计算,比如图中相同颜色的节点被至少计算了两次,因此我们可以考虑使用Memoization,将走过的结果保存起来,于是可以得到优化版的DFS:
/*
Solution: DFS + backtracking + Memoization
Time Complexity: O(n)
Space Complexity: O(n)
*/
class Solution {
public:
/*
i,j: 当前位置
w,h: 迷宫宽高
um: 备忘录
*/
int dfs(int i, int j, int w, int h, unordered_map<pair<int,int>,int, pair_hash>& um){
if(i<0||i>=h || j<0||j>=w){
return 0;
}
if(i==h-1 && j==w-1){
return 1;
}
//如果计算过该节点,直接返回结果
if(um[{i,j}] > 0){
return um[{i,j}];
}
int cr = dfs(i+1,j,w,h,um);
int cd = dfs(i,j+1,w,h,um);
um[{i,j}] = cr+cd;
//将结果放到备忘录中
return um[{i,j}];
}
int uniquePaths(int m, int n) {
//创建一个备忘录
unordered_map<pair<int,int>,int,pair_hash> um;
return dfs(0,0,m,n,um);
}
};
在引入Memoization后,解决了节点重复计算的问题,算法执行时间从指数级别降低到线性时间,即O(mxn)。但总的来说上述DFS算法依旧是自顶向下的思维方式,即从起点出发,向终点走,穷举所有可能的情况,这种思维方式是符合人类习惯的,我们可通过引入备忘录的方式来提高算法效率,如果能做到这一步已经很不错了,接下来我们将讨论如何使用动态规划的思考方式解决上面的问题。
- 使用DP
首先我们需要转变思维方式,上面解法是自定向下的搜索,如果我们反过来想,从终点出发,向前进行自底向上的递推,效果会是怎么样呢?
如果从终点出发,则原问题的解将变为:“如果要到达(m,n),需要先到达(m-1,n),或者到达(m,n-1),那么到达终点的路径数就等于到达(m,n-1)加上到达(m-1,n)的路径数”。有了原问题,接下来我们要思考该原问题是否可划分为相同的子问题,显然,对于棋盘上的每个点,均可以按照上述思路进行计算,因此原问题的解可划分若干个子问题的解,符合DP解题的条件。对每个点应用上面的计算公式,则可得出状态转移方程:
以m=3,n=3为例,则到达每个点的路径数如下所示,例如到达(1,2)和(2,1)两个点的路径数均为3,显然这也是一个局部最优解,或者说是一个最优子结构。
/*
Solution: DP
Time Complexity: O(n)
Space Complexity: O(n)
*/
/*
m=3, n=3
---------------
| 0 | 1 | 1 |
|---|----|----|
| 1 | 2 | 3 |
|---|----|----|
| 1 | 3 | 6 |
---------------
*/
int uniquePaths(int m, int n) {
if(m == 0 || n == 0){
return 0;
}
if( m == 1 || n == 1){
return 1;
}
vector<vector<int>> dp(n,vector<int>(m,1));
for(int x=1;x<n;x++){
for(int y=1; y<m; y++){
dp[x][y] = dp[x-1][y] + dp[x][y-1];
}
}
return dp[n-1][m-1];
}
通过DP我们同样将一个时间复杂度为指数级的蛮力算法转化成了一个线性时间的O(mxn)算法,性能得到了非常大的提升。但必须要承认的是,这种思考方式非常反直觉,极不容易想到,需要反复训练才能习得,如果你能够一开始就想到这种算法,那么要恭喜你,你已经具备了所谓的“计算机思维”,即像计算机一样的思考模式。
两点启发
这两个例子在本质上是相同的,它给我们启示我觉得至少有两点:
-
如果一个问题可以用递归树来描述,并且在递归树中有大量的重复计算的节点,那么我们可以引入备忘录,来缓存每一步的计算结果,这样可以使得算法的时间复杂度从指数级下降到线性,因此理解DP的一个角度为:
\[DP \approx Recursion + Memoization\] -
如果说蛮力的搜索算法是从“源头”出发的正向过程,那么DP的思路则是从“终局”出发的反向过程。这里所谓的反向是指从终点向前推进,将“终局”问题化成与之相等价的,规模更小的子问题。因此,当我们遇到需要蛮力解决的搜索问题时,不妨试着从后向前想,看能否找到突破口。但需要注意的是,不是所有的DP问题都是由终点向原点递推,递推方式取决于子问题的划分方式。
但是上面两个例子同样也会给人造成一种错觉,即DP就是在原来算法的基础上增加备忘录(缓存)来减少重复计算。实际上DP的精髓不只是解决重复计算的问题,在下面的例子中我们将会看到如何使用动态规划来求解最优化问题。
最长上升子序列(LIS)
求解上升子序列是另一个动态规划中比较经典的NP问题,问题如下:
一个数的序列ai,当a1 < a2 < … < aS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N。比如,对于序列(5,7,4,-3,9,1,10,4,5,8,9,3),有它的一些上升子序列,如(5, 7), (-3, 1, 4)等等。这些子序列中最长的长度是6,比如子序列(-3,1,4,5,8,9)。你的任务,就是对于给定的序列,求出最长上升子序列的长度。
-
将原问题拆解成若干个子问题
按照DP解题的思路,第一步还是划分子问题,这次的子问题相对来说还比较好想出来,即原问题是求解整个序列的LIS长度,那么子问题可以定义为求解某个子序列的LIS长度。为了存放每个子序列的LIS长度,我们需要一个数组
L,其中L[i]用来存放每个子序列的LIS长度值。 -
尝试计算
L[i]虽然我们知道了子问题的大概模样,但是对子问题的很多细节还不是很清楚,比如:(1)如何划分子序列?(2) 子序列的LIS值
L[i]怎么计算?(3)得到子序列的LIS值后,这个值和原序列的LIS值有什么对应关系?为了解答这些问题,我们不妨从第一个字符开始向后搜索,看看是否能找出一些规律。假设子序列为a[0..i],L[i]表示到第前i个字符(包括a[i])前的LIS长度值,接下来我们我们可以来观察一下L[i]的值:a[i] = | 5 | L[i] = | 1 | //LIS: 5 a[i] = | 5 | 7 | L[i] = | 1 | 2 | //LIS: 5,7 a[i] = | 5 | 7 | 4 | L[i] = | 1 | 2 | 2 | //LIS: 5,7 a[i] = | 5 | 7 | 4 | -3 | L[i] = | 1 | 2 | 2 | 2 | //LIS: 5,7 a[i] = | 5 | 7 | 4 | -3 | 9 | L[i] = | 1 | 2 | 2 | 2 | 3 | //LIS: 5,7,9 ... a[i] = | 5 | 7 | 4 | -3| 9 | 1 | 10 | 4 | 5 | 8 | L[i] = | 1 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | ? | //LIS: 5,7,9,10此时当
a[i]=8时,根据我们追踪的LIS序列,8<10, 因此LIS不应该追加,但此时我们发现LIS不止一个,除了5,7,9,10之外,还有另一个-3,1,4,5,而8可以附加在该LIS之后,新的LIS序列变成了-3,1,4,5,8,如下图所示:a[i] = | 5 | 7 | 4 | -3| 9 | 1 | 10 | 4 | 5 | 8 | L[i] = | 1 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | // LIS2: -3,1,4,5,8接下来
a[i]=9,我们发现之前的5,7,9,10不满足条件,而新发现的-3,1,4,5,8可以继续追加,因此接下来我们只需要维护-3,1,4,5,8,9,如下图所示:a[i] = | 5 | 7 | 4 | -3| 9 | 1 | 10 | 4 | 5 | 8 | 9 | L[i] = | 1 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 6 | //LIS2: -3,1,4,5,8,9到这里,我们似乎发现了一个问题,最新得到的
-3,1,4,5这个序列并不是我们最开始跟踪的LIS序列,而是我们无意之间发现的,假设序列a[i]继续扩展,可能又有我们没有跟踪的LIS比目前这个解更优。因此,想要保证不漏掉可能的最优解,我们不能只选定一个LIS进行跟踪,而是需要动态的计算出当前位置的最优LIS。如何才能得到
a[i]位置的最优LIS呢?我们先来思考一下为什么前面会漏掉[-3,1,4,5]这个最优解。不难看出,前面的思路是一种贪心策略,即每次都拿a[i]和LIS序列的末尾进行比较,如果a[i]大,则追加到LIS序列后面,但是如果a[i]小呢?上面的推导并没有考虑这种情况,实际上当a[i]小于LIS末尾元素时,仍有可能产生一个以比原LIS更优的解,而贪心并不能够让我们得到全局最优解。举个例子,上面数组中在
a[7]=4之前的(包括a[7])LIS序列有[5,7,9,10]和[-3,1,4],根据最优原则,显然[5,7,9,10]为最优解。接着当a[8]出现时,LIS序列变为了[5,7,9,10]和[-3,1,4,5],根据最优解原则,由于二者长度相同,末尾最小的一个最优,因此最优的LIS变成了[-3,1,4,5]。这个例子可以看出,一个数组的LIS最优解是在不断在变化的,为了选出最优解则需要计算所有以
a[i]结尾的全部LIS序列,然后选出a[i]位置上最优的一个解,更新到L[i],我们只需要不断循环这个过程,直到数组末尾即可找到最优的LIS序列。上面过程有些烧脑,此时可以停下来,再想一遍上述过程,如果想通了,我们可以接下来再重新推导一遍
L[i]。 -
再次尝试计算
L[i]如果理解了上面的逻辑,接下来我们需要重新梳理一下子问题的定义,即对任意以
a[i]结尾的子序列,找到所有LIS序列,并从中找到最优的一个;所谓最优是指:(1)长度最长 (2)同等长度下,末尾数字更小。接下来我们可以重新推演一遍
L[i]:a[i] = | 5 | L[i] = | 1 | //LIS: 5 a[i] = | 5 | 7 | L[i] = | 1 | 2 | //LIS: 5,7 a[i] = | 5 | 7 | 4 | L[i] = | 1 | 2 | 1 | //以4结尾的LIS只有4自己 a[i] = | 5 | 7 | 4 | -3 | L[i] = | 1 | 2 | 1 | 1 | //以-3结尾的LIS只有-3自己 a[i] = | 5 | 7 | 4 | -3 | 9 | L[i] = | 1 | 2 | 1 | 1 | 3 | //以9结尾的最优LIS为[5,7,9] ... a[i] = | 5 | 7 | 4 | -3| 9 | 1 | 10 | 4 | 5 | 8 | L[i] = | 1 | 2 | 1 | 1 | 3 | 2 | 4 | 3 | 4 | ? |此时又到了
a[i]=8的位置,这时L[i]的值应该为多少呢?按照子问题的定义,需要找到以8为结尾的最优LIS,显然以9或10结尾的最优LIS是不能追加8的,因此刨除9,10候选剩下的L[i]中最大的是L[8]=4,此时a[8]=5,可以追加8,因此a[i]=8位置的最优LIS长度为5,即L[9]=5
-
确定递推公式
通过上面的推演,我们现在可以很容易的写出
L[i]的递推公式了。对于任意的L[i]我们需要做两件事:- 找到在
a[0..i-1]中需要比a[i]小的数 - 在这些数中找到对应的
L[i]的值最大的x = max(L[0..i-1]),则L[i]的值为x+1
在得到完整的
L[i]数组后,题目的最终解即为max(L)。代码如下:def lis(self, nums): n = len(nums) if n == 0: return 0 if n == 1: return 1 l = [0]*n; l[0]=1 for i in range(1,n): tmp = 0 for j in range(0,i): if nums[j] < nums[i] and l[j] > tmp: tmp = l[j] l[i] = tmp + 1 return max(l) - 找到在
DP和贪心回溯的关系
- 如果待求解问题不具备最优子结构,没有中间过程可以缓存,没有可以被优化的重复计算,则只能通过暴力枚举进行求解,此时适合用深搜+回溯
- 贪心法是每一步都求局部最优解,默认每一步都具有最优子结构,如果全局最优解可以被这样一步步推出来,则该问题可用贪心法求解。贪心实际上是DP问题的一个特例,它对子问题的要求比较严格,它要求子问题具有”无后效性“,即当前选择永远最优,后面的选择不能影响到前面的选择。
- DP更像是回溯和贪心的结合版,当回溯存在大量重复计算时,我们可以将中间结果缓存起来,并用这些局部最优解计算全局最优解。当贪心策略不再局限眼前利益时,它的递推公式就变成了DP的状态转移方程。
Resources
- MIT 6.006 Introduction to Algorithms, Fall 2011
- MIT 6.046J Design and Analysis of Algorithms, Spring 2015
- CS106B-Stanford-YouTube
- Algorithms-Stanford-Cousera
- 算法与数据结构-1-北大-Cousera
- 算法与数据结构-2-北大-Cousera
- 算法与数据结构-1-清华-EDX
- 算法与数据结构-2-清华-EDX
- 算法设计与分析-1-北大-Cousera
- 算法设计与分析-2-北大-EDX
