理解iOS中的Quartz2D

对于Quartz我觉得有两个点值得讨论：一是坐标系，二是绘制bitmap

坐标系

如果熟悉openGL，那么对Quartz的坐标系相信不会有太多的疑惑。Quartz的坐标系是二维的坐标系，通过CGAffineTransform的状态矩阵来表示，顾名思义，它是一种二维线性的可逆变换，也叫仿射变换。在openGL中，物体是通过矩阵表示的，对于二维平面，只需要让z方向分量为单位向量:

这就是CGAffineTransform矩阵。在iOS中，它的定义如下：

struct CGAffineTransform {
  CGFloat a, b, c, d;
  CGFloat tx, ty;
};

这个矩阵和openGL中的矩阵表示的含义是相同的：

• a ： 水平方向的缩放
• c : 水平方向的旋转

• tx: 水平方向的位移

• b ：竖直方向的旋转
• d ：竖直方向的缩放
• ty：竖直方向的位移

如果有一个点(x,y,1)乘以这个状态矩阵，将得到新的点：

其中，如果旋转变量b,c为0的话，那么

即新的x值等于旧x值乘以缩放值 + 位移值。y同理。 如果使用Core Graphic绘制，我们可以得到一些矩阵：

// Drawing code
CGContextRef ctx = UIGraphicsGetCurrentContext();
//得到当前的状态矩阵
CGAffineTransform t0 = CGContextGetCTM(ctx);
//得到当前状态矩阵的逆矩阵
CGAffineTransform t1 = CGAffineTransformInvert(t1);
//得到单位阵
CGAffineTransform t2 = CGAffineTransformIdentity;

CTM是Current Transform Matrix的缩写，为了理解的更直观，我们从Quartz的坐标系统开始：

在Quartz的坐标系中左下角为（0，0），但是我们是用Core Graphic的api都是以左上角为(0，0)的，这中间的转换就是通过了CGAffineTransform这个状态矩阵，我们可以看一下一个普通view的CGAffineTransform矩阵：

(lldb) p t0
(CGAffineTransform) $1 = {
  (CGFloat) a = 1
  (CGFloat) b = 0
  (CGFloat) c = 0
  (CGFloat) d = -1
  (CGFloat) tx = 0
  (CGFloat) ty = 568
}

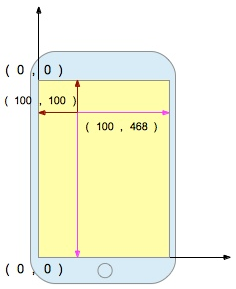
这个矩阵的意思很明确：将y轴翻转然后再向上平移568个单位，就是(0,0)了。假如我们在(100,100)画了一个点，实际上在Quartz的坐标系中，这个点是(100,468)。

改变坐标系

了解这个原理后，我们便可以随便改变坐标系，我们先在(0,0)点画个圆:

然后将坐标系的原点平移到(20,20)：

//得到单位阵
CGAffineTransform t1 = CGAffineTransformIdentity;
//平移单位阵
t1 = CGAffineTransformTranslate(t1, 20, 20);
//改变当前状态阵
CGContextConcatCTM(ctx, t1);</pre> 

得到结果如下：

这种变换不难想象其实是改变了tx,ty的偏移值：

(CGAffineTransform) $0 = {
  a = 1
  b = 0
  c = 0
  d = -1
  tx = 10
  ty = 558
}

同样我们也可以旋转坐标系：

 //旋转坐标系
 CGContextRotateCTM(ctx, (-90)*M_PI/180.0);

绘制图片

使用UIGraphicsBeginImageContextWithOptions

我们经常需要使用context绘制bitmap,Core Graphic提供了很多方法来实现它，多到令人费解。我们先看一种常用的方法：

UIImage* ret = nil;
CGSize newSize = CGSizeMake(10, 10);
UIGraphicsBeginImageContextWithOptions(newSize, NO, 0);
CGRect newRect = (CGRect){0,0,newSize};
[_img drawInRect:newRect];
ret = UIGraphicsGetImageFromCurrentImageContext();
UIGraphicsEndImageContext();

UIGraphicsBeginImageContextWithOptions这个API用来在内存中生成一个RBGA格式的Bitmap，上面代码是将原图缩小到10x10，绘制一张新图:

接下来，我们可以换一种绘图方式

CGSize newSize = CGSizeMake(10, 10);
CGRect newRect = (CGRect){0,0,newSize};

UIGraphicsBeginImageContextWithOptions(newSize, NO, 0);
CGContextRef srcContext = UIGraphicsGetCurrentContext();
CGContextDrawImage(srcContext, newRect, _img.CGImage);
CGImageRef newImgRef = CGBitmapContextCreateImage(srcContext);
UIImage* newImg = [UIImage imageWithCGImage:newImgRef];
UIGraphicsEndImageContext();

结果却是这样的：

图片为什么反了呢？熟悉图像处理的人应该知道bitmap的数据排列和显示是成镜像关系的，bitmap 数据指针指向图片的末行。因此，如果想把bitmap按照正确的顺序绘制出来，需要改变Quartz的绘制顺序，让它从从远点开始，然后从底向上绘制。

CGContextScaleCTM(srcContext, 1.0, -1.0);
CGContextTranslateCTM(srcContext, 0, -10);

上面代码的意思是坐标系反转了之后，状态矩阵变成了：

$0 = [
  a = 1
  b = 0
  c = 0
  d = 1
  tx = 0
  ty = 0
]

按照上面的计算公式，坐标变成了

x(new) = x(old)*1;
y(new) = y(old)*1;

也就是说Quartz从（0，0）点开始绘制了，读bitmap第一行像素，从屏幕最底部显示出来，这样bitmap的绘制顺序就正确了。 这种方式确实很麻烦，需要developer理解Quartz的坐标并且对bitmap图片格式也要熟悉，因此并不建议使用。

使用RenderInContext

layer.renderInContext：可以将当前layer的content变成一张CGImageRef，这和Quartz有什么关系呢？很久以前我试图render部分layer的内容到一张image，就是说给View的一部分截图。例如一个view的bounds是(0,0,100,100)，我想截取其（50，50，30，30）的部分。实现这个功能有很多种办法，最笨的就是把layer的content先通过context生成bitmap，然后去找像素点，聪明一点的就可以使用layer的二维状态矩阵。假如我们要实现下面的效果：

假设左边原图大小为100x100，待截取区域矩形的origin位于原图的(25,15)处，大小为50x50。

首先我们需要一个context，创建一个50x50的bitmap，左上角为(0,0)。然后当layer通过context渲染时，只要保证layer的(25,15)这个点在context的状态矩阵中是(0,0)即可。那么怎么做到这一点？上面有提到平移坐标系，例如上面讨论中，我们将tx，ty各增加10。那么对于UIKit的坐标系，（0，0）点便成了(10,10)点，也就是图从（10,10）开始显示。那么反推这种运算，我们现在可以将tx = -25, ty = -15，这样UIKit的坐标系，（0，0）点便成了(-25,-15)点。这样便相当于从原图的(25，15)开始绘制。

CGSize newSize = CGSizeMake(50, 50);  
UIGraphicsBeginImageContextWithOptions(newSize, NO, 0);
CGContextRef srcContext = UIGraphicsGetCurrentContext();

//得到layer的状态矩阵
CGAffineTransform m = v.layer.affineTransform;

//得到layer在context中的状态矩阵
CGContextConcatCTM(srcContext, m);

//平移UIKit坐标系
CGContextTranslateCTM(srcContext, -25, -10);

[v.layer renderInContext:srcContext];

UIImage* newImg = UIGraphicsGetImageFromCurrentImageContext();
UIGraphicsEndImageContext();

return newImg;