实现Lomo效果

Posted on 2013-11-20 | In iOS

lomo效果，是一种很流行的滤镜效果，许多开源的工程都能实现，比如很cool的GPUImage。但是想实现instagram的效果却有点难，其实从图像处理的角度出发，实现instagram的lomo效果并不复杂，难点在一些性能优化上。因此，我准备从图像处理的角度出发，从理论上实现instagram滤镜的hefe效果。

下面两张图分别为原图和instagram滤镜的hefe效果再叠加上水滴效果。

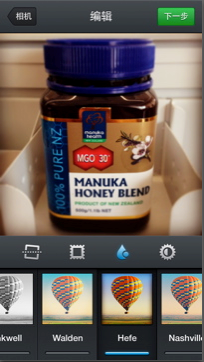
其中hefe效果也是lomo的一种，需要对原图RGB三通道分别进行非线性拉伸，实现起来比较简单。水滴效果是一种权重服从高斯分布的模糊：图片中心最清楚，边缘最模糊。

实现上面的效果要做如下几步：

找到hefe效果的map
对原图进行RGB三通道分离，根据map进行拉伸，得到新图h1
对h1进行模糊，得到模糊图像h2
计算各个像素的高斯权重a
h3 = ah1+(1-a)h2，h3为最终输出的图像

为了实现这个过程，我们不希望用Core Image或者类似的high-level的api，这种api你根本搞不清楚它里面做了什么。因此，我们用plain c code去实现这个模型，暂时不考虑性能的问题。

非线性拉伸

lomo的效果实际上是图像RGB三通道分别做非线性拉伸的效果。图像的拉伸描述了输入像素和输出像素的对应关系，一旦变换函数确定，则每一点的像素值就被确定下来：

$g\left ( x,y \right ) = T\left [ f\left ( x,y \right ) \right ]$

例如我们可以将[200~255]范围内的像素映射（map）到[50~100]，这样图像就会整体变暗，如果映射关系是符合线性的，那么就成为线性拉伸，如果映射关系是非线性的，就称为非线性拉伸。

接下来我们的任务便是找到hefe效果的非线性映射的曲线，如果身边有设计师，可以让他们用PS调出hefe的效果，然后我们拿到它的RGB三通道的曲线：

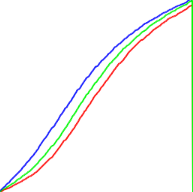
途中红色为R通道，绿色为G通道，蓝色为B通道，从曲线的变化来看，是一种非线性关系。

接下来，我们可以根据上面的曲线产生一张离散的map表：

static UInt8 hefemap[]= 
{0,0,0,255,
0,0,1,255,
1,1,2,255,
1,2,3,255,
2,2,4,255,
2,4,5,255,
3,4,6,255,
.........}

表中4个字节为一组，分别为R,G,B,A。例如：

R通道中，0映射成0，1映射成0，2映射成1，3映射成1… G通道中，0映射成0，1映射成0，2映射成1，3映射成2… B通道中，0映射成0，1映射成1，2映射成2，3映射成3… A是alpha值，没变化为255

这种将RGB混在一起的去存储显然不直观，我们对hefemap进行RGBA通道的分离：

void createMappedRGBChannels()
{
    for(int i = 0; i < 256; i++) {
        rByte[i] = hefemap[i*4];
        gByte[i] = hefemap[i*4+1];
        bByte[i] = hefemap[i*4+2];
        aByte[i] = hefemap[i*4+3];
    }
}

这样rByte,gByte,bByte,aByte便分别保存了RGBA各个通道的映射关系，到此，hefe效果已经实现一半了。接下来我们便可以拉伸原图了：

//r,g,b map映射
UInt8 r,g,b,a;
for (int i=0; i<srcBitmapHeight*srcBitmapRowBytes; i+=4) {

			r                  = srcBitmapData[i];
			g                  = srcBitmapData[i+1];
			b                  = srcBitmapData[i+2];
			a                  = srcBitmapData[i+3];
			
			srcBitmapData[i]   = rByte[r];
			srcBitmapData[i+1] = gByte[g];
			srcBitmapData[i+2] = bByte[b];
			srcBitmapData[i+3] = rByte[a];

}

首先我们把原图画出来，context指向了一块bitmap，然后根据我们刚才生成的映射表来改变bitmap中的像素点，最后把改变后的图片画出来。我们还以经典的lena256x256.png为例，左边是原图，右边是hefe拉伸的效果：

到此，我们已经实现了上面5步中的前两步。

模糊

接下来我们要实现第三步，也就是模糊图像。

模糊图像可以有很多种方式来实现，现在比较流行是高斯模糊，为了简单起见，我们就用前一篇文章提到的均值模糊来实现：

vImageBoxConvolve_ARGB8888(effectInBuffer, effectOutBuffer, NULL, 0, 0, 25, 25, bgColor, kvImageEdgeExtend);

模糊结果如下：

右图为模版5x5的均值模糊结果。

计算高斯权重

接下来是第四步，计算高斯权重。由于我们要实现的效果是以图片中心为最清楚的点，到图片四周以此模糊，最边缘的像素最模糊。实现这个效果，要求模糊要过度的很自然，因此我们就想到了使用正态分布。在retina上，上面的图片大小为1024*1024像素，因此我们要计算各个像素到(512,512)这个点的权重，越近的点自然权重越高，也就越清楚，越远的点则权重越低，越模糊。我们用二维高斯函数:

$G(u,v) = \frac{1}{2\pi \sigma^2} e^{-(u^2 + v^2)/(2 \sigma^2)}$

考虑到权重在0-1之间，我们用归一化的式子：

$G(u,v) = e^{-(u^2 + v^2)/(2 \sigma^2)}$

这时候，不确定的值就是sigma，关于sigma取多少，基本上是通过不断尝试来找出一个经验值，我们先来实现它，然后再讨论sigma的值：

int rx,ry = 0;
double sigma = 300;
for (int i=0; i<1024; i++)
{
   for (int j=0; j<1024; j++) {
       
       rx = j-512;
       ry = i-512;
       wByte[i][j] = exp(-0.5*(pow(rx, 2)+pow(ry, 2))/pow(sigma, 2));
       
   }
}

忽略性能和内存上的问题，首先开辟了一个wByte[1024][1024]来保存每个点的权重（当然这也不是个好办法，由于图片是正方对称的，理论上使用1/4的空间就足够了），然后根据二维高斯公式计算一个1024x1024的矩阵中各个点掉(512,512)的距离，最后将权重值保存下来。这时候我们来讨论sigma，基本上，sigma值取的越大，高斯分布峰值覆盖的范围就越大，中心处清楚的面积就越大，反之，sigma值越小，峰值覆盖的范围就越小，中心处清楚的面积就越小。

图像融合

权重值也有了，我们就差最后一步了，也很简单。根据上面第5步的式子，我们首先需要两个context指向两块bitmap，第一块是hefe效果的bitmap，第二块是将hefe模糊的bitmap。然后根据公式，分别在RGB三通道计算新的像素值，最后再画一幅新的图片：

int w_x,w_y = 0.0;
float w = 0.0f;

for (int i=0; i<srcBitmapHeight*srcBitmapRowBytes; i+=4) {
    
    w_x = (i%srcBitmapRowBytes)/4;
    w_y = i/srcBitmapRowBytes;
  
    w = wByte[w_x][w_y];
    
    srcBitmapData[i]   = srcBitmapData[i]*w  + (1-w)*blurBitmapData[i];
    srcBitmapData[i+1] = srcBitmapData[i+1]*w + (1-w)*blurBitmapData[i+1];
    srcBitmapData[i+2] = srcBitmapData[i+2]*w + (1-w)*blurBitmapData[i+2];
}

CGImageRef newImgRef = CGBitmapContextCreateImage(srcContext);
UIImage* newImg = [UIImage imageWithCGImage:newImgRef];
UIGraphicsEndImageContext();
return newImg;

结果如下：

最后边的一张为最后的结果，效果和我们预期的一致：中心一圈最清楚（半径根据sigma调整），向外侧依次模糊，最外面一圈最模糊。

后面我们可以通过调整sigma的值来控制模糊的权重值，从而达到我们想要的效果。

至此，我们实现了lomo效果的原型，我们看到，代码简简单单，又很少，但是上面的代码仅仅是个demo。实际应用的的时候不仅算法需要优化，显示也需要交给openGL，我们在后面再来讨论如何用openGL实现上面的效果。

（全文完）