首页 | Home
博客 | Blog
关于 | About

Lexical Analysis & Finate Automata

Posted on | In Compiler

Lexical Analysis

  • 词法分析
    • 将代码分解成token.
  • Token Class（Token的类型）:
    • Identifier:以英文字母开头, A1,Foo,B17,….
    • Integer:一串非空的数字, 0,12,001,…
    • keyword:if,else,begin,…
    • whitespace: 空格，换行，tab等
  • Token格式：
    • <class:string>
  • LA的输入是一串字符串，LA输出的是一系列token的数组
    • 例如输入是: foo=42;
    • 输出是:<identifier,"foo">, <op,"=">, <int,"42">
  • 总结一下LA要做两件事：
    • 检查substring中包含的token
    • 每个token生成<class:string>的格式

Lexical Analysis example

  • FORTRAN :
    • 空格不记入token
      • VA R1 = VAR1
      • DO 5 I = 1.25的意思是变量DO51的值为1.25
    • 在FORTRAN中，循环：DO 5 I = 1,25 意思是在DO符号开始处和符号5(类似goto的label)之间的语句是循环体,变量从I的值从1到25
    • 问题: LA是如何判断等号左边是变量赋值语句还是循环语句？
      • LA检测token的顺序是从左到右，这时它涉及到 look ahead,当LA发现DO时，它会look ahead去看等号后面是逗号还是点。类似的情况还有if,else等这种关键字，=,==这种操作符，当LA检测到首字母时并不能确定它是变量名称还是关键字或操作符，因此LA需要look ahead。
      • 因此在设计LA的时候要尽量避免这种look ahead，会影响性能。
    • FORTRAN有这种funny rule，是因为那个时候很容易不小心打出空格
  • C++:
    • C++的模版语法：Foo<Bar>
    • C++的IO输入语法：cin>>var
    • 如果碰到:Foo<Bar<Bazz>>怎么办？, 最后的>>怎么判断呢？
    • C++的LA解决办法是，让developer手动加一个空格：Foo<Bar<Bazz> >(现在的编译器已经修复了该问题)

Regular Languages

  • Lexical structure = token classes
    • each one of the token classes contains a set of strings
  • We must say what set of strings is in a token class
    • 当拿到了n多个token之后，需要用正则式匹配出该token属于那种类型(token class)
    • 寻找token class的方法一般是使用regular langauages
  • 什么是Regular Language:
    • 正则语言
    • 定义Regular Language是通过一系列正则表达式来构成的(Regular Expression):
      • 每一种正则表达式代表一种字符集，有两种基本的字符集：
        • Single character:
          • 'c' = {"c"}:表示只含有这个字符的字符集
        • Epsilon:
          • ε = {""}: 表示只包含一个空字符串的字符集
          • 注意ε不等于o(empty)
      • 除了这两种基本的字符集外，还有三种组合型的字符集:
        • Union
          • A+B = {a|a<A} or {b|b<B}
        • Concatenation
          • AB = {ab|a<A and b<B}
        • Iteration
          • A* = AAA....A(重复i次)
          • 如果i=0，那么上面式子变成A0，A0 = e(Epsilon) = {""}
      • 正则表达式：在某个字符集(假如为Z)上，有一个最小的表达式集合，通过这个集合可以表征Z上任意字符的组合（可能的出现情况）。正则表达式的y语法（grammar）如下
        • Baes cases
          • R = ε = {""}(epsilon)
          • R = {c}, c属于某个字符集Z，例如字母表
        • Three compound expressions
          • Union: R = R+R
          • Concatenation: R = RR
          • Iteration: R = R*
      • 正则表达式的例子:
        • 假设字符集Z = {0,1}
          • 1* 表示 "" + 1 + 11 + 111 + 111...1(i次) = all strings of 1’s，意思是1*这个正则表达式可以表示所有1的字符。
          • (1+0)1等价于{ab|a<1+0 and b<1} = {11,01}，意思是(1+0)1这个正则表达式可以表示{11,01}这两种情况的字符串
          • (0+1)* = "" + (0+1) + (0+1)(0+1) + ... + (0+1)...(0+1) = all string of 1’s and 0’s。意思是这个正则表达式可以表示字符集Z的任意字符组合。
          • 表征同一字符集的正则表达式有不止一个，例如第1个例子1*也可以写作1* +1 第2个例子也可以写作11+10。
  • 小结
    • 正则表达式是定义正则语言的基础
    • 正则表达式的基础语法有5条
      • Two base cases
        • an empty character - ε
        • a single character
      • Three compound expressions
        • union, concatenation, iteration

Formal Languages

  • Formal language是计算机编程语言理论的基础，上一节提到的Regular Language也是是Formal Language的一种
  • 定义
    • 假设 $\sum$ 是一个字符集，Formal Languages是指建立在这个字符集之上的语言
      • Not well-defined Formal Languages
        • Alphabet = English characters, Language = English sentences
      • Well-defined Formal Languages
        • Alphabet = ASCII, Language = C programs
    • 不同的语言是建立在不同的字符集上，因此讨论某种Formal Language的前提是先确定其所在的字符集合

Meaning Function

  • 每种Formal Language都有Meaning function

    • L maps syntax to semantics(将表达式转换为语义)

      \[L(e) \thinspace = \thinspace M\]

      例如，对于正则语言来说，e为正则表达式，M为它所表示的一组字符串

    • 对于正则语言来说，e为正则表达式，M为其所匹配的字符串集合，

      • L(ε) = {""}
      • L('c') = {"c"}
      • L(A+B) = L(A) or L(B)
      • L(AB) = {ab| a<L(A) and b<L(B)}
      • L(A*) = {"",A,AA,...,A...A}
  • 为什么要定义meaning function？
    • Makes clear what is syntax, what is semantics
    • Allows us to consider notation as a separate issue ,分离语法(e)和语义(L(e))
    • Because expressions and meanings are not 1-1, 描述同一字符集的正则表达式不唯一
      • 例如0*表示{"",0,00,...}该集合也可以用0+0*来描述
    • 对应到编程语言
      • 表征同一语义的语法可以有很多，但是处理后得到的语义是相同的
      • 不同变成语言定义变量的方式不同，但其语义均为在内存中定义一个变量
    • Meaning function L是多对一的

Lexical Specifications

  • 语言关键字（keyword）的正则表示
    • 正则： 'i''f' + 'e''l''s''e'
    • 简化： 'if' + 'else' + 'then' + ...
  • 数字的正则表示
    • 单个integer的正则：digit = '0'+'1'+'2'+'3'+...+'9'
    • 至少有一个非空符号的正则：AA* = A+
      • 对于数字来说，它的正则为:digit digit* = digit+ = [0-9]+
  • 变量，字符（identifier）的正则表示
    • 字符: 'a'+'b'+'c'+...+'z'+'A'+'B'+...+'Z'
      • 简化上面的正则，使用range:[]符号:[a-zA-Z]
      • 总的正则letter(letter + digit)* = [a-z][A-Z]*
  • whitespace: a non-empty sequence of blanks, newlinke, and tabs
    • blanks : ' '
    • new line: \n
    • tabs: \t
    • 总的正则: (‘ ’+‘\n’+'\t')+
  • anyone@cs.standford.edu
    • 正则为letter+‘@’+letter+'.'+letter+'.'+letter
    • [a-zA-Z]+@[a-zA-Z]+.
  • PASCAL的数字token正则式
    • digit = '0'+'1'+...+'9'
    • digits = digit+
    • opt_fraction = ('.'digit) + e
    • opt_exponent = ('E'('+'+'-'+e) digits) + e
    • num = digits opt_fraction opt_exponent

DFA

我们先从正则表达式开始说，正则表达式的理论基础为有限状态机，具体来说是DFA和NFA，参考之前编译原理的文章，一个DFA至少要包含下面五部分

  1. 一个确定的状态集合，用 $Q$ 表示
  2. 一组输入的字符，用 $\sum$ 表示
  3. 一个状态转移函数（正则表达式），用 $\delta$ 表示
  4. 一个初始状态，用 $q_0$ 表示，$q_0$ 属于 $Q$ 的一部分
  5. 一组最终状态(Final State)，用 $F$ 表示，$F \subseteq Q$，也可以叫Accepting State

例如，正则式r='a+1+'对应的DFA状态图为

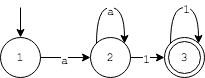
我们可以用一段Python代码来模拟上述DFA的工作过程：

#定义状态转义函数
edges = {
    (1,'a') : 2, #state#1 takes an input of 'a', transfer the state to #2
    (2,'a') : 2,
    (2,'1') : 3,
    (3,'1') : 3
}
#定义状态机的结束状态，可能有多个结束状态，用array表示
accepting = [3]

#string: 输入字符
#current: 当前状态/初始状态
#edges: 状态转移方程
#accepting: 最终状态集合
def fsmsim(string, current, edges, accepting):
    if string == "":
        #递归基，如果当前字符处于Accepting State则终止递归，匹配结束
        return current in accepting
    else:
        letter = string[0]
        key = (current,letter)
        #进入状态机
        if key in edges:
            next_state = edges[key]
            remaining_string = string[1:]
            #递归
            return fsmsim(remaining_string,next_state,edges,accepting)
        else:
            return False;

#test - case:
print(fsmsim("aaa111",1,edge,accepting)) #=>True 
print(fsmsim("a1a1a1",1,edge,accepting)) #=>Flase
print(fsmsim("",1,edge,accepting)) #=>False

回顾一下上面的过程，其思路为:

  1. 由正则式构造出FSM状态机， 状态转移方程用map<tuple<int,char>,int>表示
  2. 设计fsm函数，解析输入字符串
  3. 观察输入字符串是否匹配正则式（能被状态机接受）

为了加深理解，接下来再来看几个例子，令上述的正则式分别为r"q*"和r"[a-b][c-d]?"，则FSM状态机变为（分别对应左图和右图）：

左图的正则式比较好理解，表示字母q重复出现0次或者多次，右图的正则式表示第一个字符是a或者b，第二个字符是c或者d(也可能没有第二个字符)。上述两个正则式对应状态转移函数分别为:


edges = {
    (1,'q'):1
}
acpt = [1]


# test-case
print fsmsim("",1,edges,acpt) #True
print fsmsim("q",1,edges,acpt)#True
print fsmsim("qq",1,edges,acpt)#True
print fsmsim("p",1,edges,acpt)#False



edges = {
    (1,'a'):2,
    (1,'b'):2,
    (2,'c'):3,
    (2,'d'):3
}
acpt = [2,3]
#test-case
print fsmsim("a",1,edges,acpt)#True
print fsmsim("b",1,edges,acpt)#True
print fsmsim("ad",1,edges,acpt)#True
print fsmsim("e",1,edges,acpt)#False

NFA

Python的re库对正则表达式解析和fsmsim类似，但是上面的fsmsim函数只是实现DFA，没有考虑NFA，具体来说有下面两种情况没有考虑

  1. Ambiguity
  2. $\epsilon$ 状态

考虑下面NFA，输入字符串为1-23

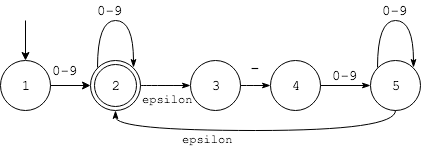
  1. 从状态起始点#1开始，输入字符为1，走到状态#2
  2. 由于有$\epsilon$ 状态，#2可以直接转化为状态#3
  3. 状态#3读入-进入状态4
  4. 状态#4读入2进入状态5
  5. 状态#5读入3之后，产生Ambiguity，一种可能是回到状态#2，一种可能是停留在#5

不难看出，产生Ambiguity的一个原因是正则式里存在”或”。再来看一个例子，有正则式为a+|ab+c，由于有|，因此第一个状态后就出现了分支

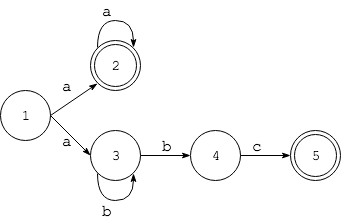
回忆前面对FSM的python描述，每一组<状态,输入>的Tuple对应唯一个next_state，对于NFA，next_state可能有多个，对此，我们需要遍历next_states中的所有情况，相应的fsm函数也需要修改:

edges = { (1, 'a') : [2, 3],
          (2, 'a') : [2],
          (3, 'b') : [4, 3],
          (4, 'c') : [5] }
accepting = [2, 5] 

def nfsmsim(string, current, edges, accepting): 
    if(string==""):
        return current in accepting
    else:
        letter = string[0]
        key = (current,letter)
        if key in edges:
            next_states = edges[key]
            for state in next_states:
                remain_str = string[1:]
                #只有当nfsmsim为true 才返回，false继续尝试
                if nfsmsim(remain_str,state,edges,accepting):
                    return True
        
        return False

# test case
print "Test case 1 passed: " + str(nfsmsim("abc", 1, edges, accepting) == True) 
print "Test case 2 passed: " + str(nfsmsim("aaa", 1, edges, accepting) == True) 
print "Test case 3 passed: " + str(nfsmsim("abbbc", 1, edges, accepting) == True) 
print "Test case 4 passed: " + str(nfsmsim("aabc", 1, edges, accepting) == False) 
print "Test case 5 passed: " + str(nfsmsim("", 1, edges, accepting) == False)

参考之前计算理论的文章可知，对所有NFA都可以转化而为DFA，下图NFA对应的正则表达式为ab?c

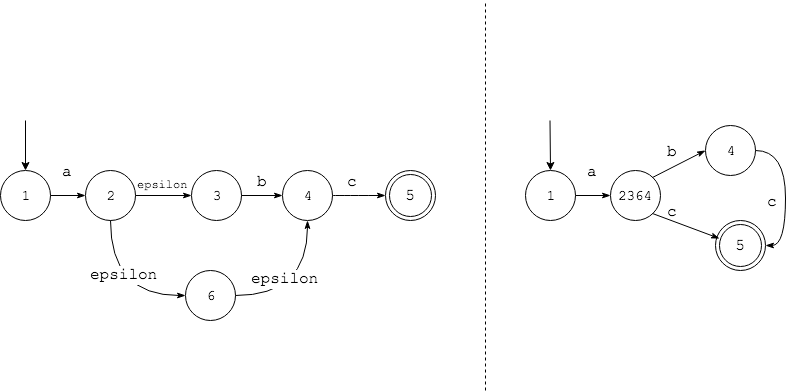
左边的NFA是对上述正则表达式的一种很直观的实现，右边是与其等价的DFA，它将所有通过epsilon所到达的状态进行了合并，解决了上述两个问题。

小结

  1. string是一组字符的合集
  2. 每个Regular Expression对应一个DFA，反之亦然
  3. NFA可以转化为DFA
  4. 使用fsmsim函数来实现regular expression的解析

在实际的解析过程中，我们几乎不会用到fsmsim函数，而是直接使用正则表达式，但了解其如何工作的对理解Parser很重要，接下来我们将讨论如何如何实现词法分析，将表达式切分成token