词法分析

Posted on 2017-02-10 | In Parser , Compiler

Prerequist Knowledge

Automata Theory
- Finite State Machine
- Formal Language
- Regular Language
- Context Free Grammar
- DFA / NFA
Lexcial Analysis
Algorithms
- Recursion
Tools
- Python Syntax
- Python Lex-Yacc
- Regular Expression

DFA

我们先从正则表达式开始说，正则表达式的理论基础为有限状态机，具体来说是DFA和NFA，参考之前编译原理的文章，一个DFA至少要包含下面五部分

一个确定的状态集合，用 $Q$ 表示
一组输入的字符，用 $\sum$ 表示
一个状态转移函数（正则表达式），用 $\delta$ 表示
一个初始状态，用 $q_0$ 表示，$q_0$ 属于 $Q$ 的一部分
一组最终状态(Final State)，用 $F$ 表示，$F \subseteq Q$，也可以叫Accepting State

例如，正则式r='a+1+'对应的DFA状态图为

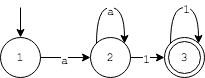
我们可以用一段Python代码来模拟上述DFA的工作过程：

#定义状态转义函数
edges = {
    (1,'a') : 2, #state#1 takes an input of 'a', transfer the state to #2
    (2,'a') : 2,
    (2,'1') : 3,
    (3,'1') : 3
}
#定义状态机的结束状态，可能有多个结束状态，用array表示
accepting = [3]

#string: 输入字符
#current: 当前状态/初始状态
#edges: 状态转移方程
#accepting: 最终状态集合
def fsmsim(string, current, edges, accepting):
    if string == "":
        #递归基，如果当前字符处于Accepting State则终止递归，匹配结束
        return current in accepting
    else:
        letter = string[0]
        key = (current,letter)
        #进入状态机
        if key in edges:
            next_state = edges[key]
            remaining_string = string[1:]
            #递归
            return fsmsim(remaining_string,next_state,edges,accepting)
        else:
            return False;

#test - case:
print(fsmsim("aaa111",1,edge,accepting)) #=>True 
print(fsmsim("a1a1a1",1,edge,accepting)) #=>Flase
print(fsmsim("",1,edge,accepting)) #=>False

回顾一下上面的过程，其思路为:

由正则式构造出FSM状态机，状态转移方程用map<tuple<int,char>,int>表示
设计fsm函数，解析输入字符串
观察输入字符串是否匹配正则式（能被状态机接受）

为了加深理解，接下来再来看几个例子，令上述的正则式分别为r"q*"和r"[a-b][c-d]?"，则FSM状态机变为（分别对应左图和右图）：

左图的正则式比较好理解，表示字母q重复出现0次或者多次，右图的正则式表示第一个字符是a或者b，第二个字符是c或者d(也可能没有第二个字符)。上述两个正则式对应状态转移函数分别为:


edges = {
    (1,'q'):1
}
acpt = [1]


# test-case
print fsmsim("",1,edges,acpt) #True
print fsmsim("q",1,edges,acpt)#True
print fsmsim("qq",1,edges,acpt)#True
print fsmsim("p",1,edges,acpt)#False


edges = {
    (1,'a'):2,
    (1,'b'):2,
    (2,'c'):3,
    (2,'d'):3
}
acpt = [2,3]
#test-case
print fsmsim("a",1,edges,acpt)#True
print fsmsim("b",1,edges,acpt)#True
print fsmsim("ad",1,edges,acpt)#True
print fsmsim("e",1,edges,acpt)#False

NFA

Python的re库对正则表达式解析和fsmsim类似，但是上面的fsmsim函数只是实现DFA，没有考虑NFA，具体来说有下面两种情况没有考虑

Ambiguity
$\epsilon$ 状态

考虑下面NFA，输入字符串为1-23

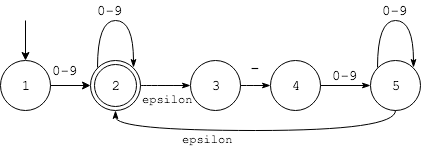
从状态起始点#1开始，输入字符为1，走到状态#2
由于有$\epsilon$ 状态，#2可以直接转化为状态#3
状态#3读入-进入状态4
状态#4读入2进入状态5
状态#5读入3之后，产生Ambiguity，一种可能是回到状态#2，一种可能是停留在#5

不难看出，产生Ambiguity的一个原因是正则式里存在”或”。再来看一个例子，有正则式为a+|ab+c，由于有|，因此第一个状态后就出现了分支

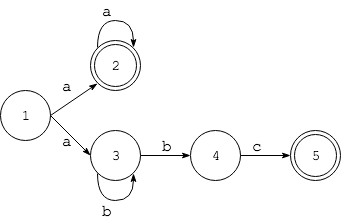
回忆前面对FSM的python描述，每一组<状态,输入>的Tuple对应唯一个next_state，对于NFA，next_state可能有多个，对此，我们需要遍历next_states中的所有情况，相应的fsm函数也需要修改:

edges = { (1, 'a') : [2, 3],
          (2, 'a') : [2],
          (3, 'b') : [4, 3],
          (4, 'c') : [5] }
accepting = [2, 5] 

def nfsmsim(string, current, edges, accepting): 
    if(string==""):
        return current in accepting
    else:
        letter = string[0]
        key = (current,letter)
        if key in edges:
            next_states = edges[key]
            for state in next_states:
                remain_str = string[1:]
                #只有当nfsmsim为true 才返回，false继续尝试
                if nfsmsim(remain_str,state,edges,accepting):
                    return True
        
        return False

# test case
print "Test case 1 passed: " + str(nfsmsim("abc", 1, edges, accepting) == True) 
print "Test case 2 passed: " + str(nfsmsim("aaa", 1, edges, accepting) == True) 
print "Test case 3 passed: " + str(nfsmsim("abbbc", 1, edges, accepting) == True) 
print "Test case 4 passed: " + str(nfsmsim("aabc", 1, edges, accepting) == False) 
print "Test case 5 passed: " + str(nfsmsim("", 1, edges, accepting) == False) 

参考之前计算理论的文章可知，对所有NFA都可以转化而为DFA，下图NFA对应的正则表达式为ab?c

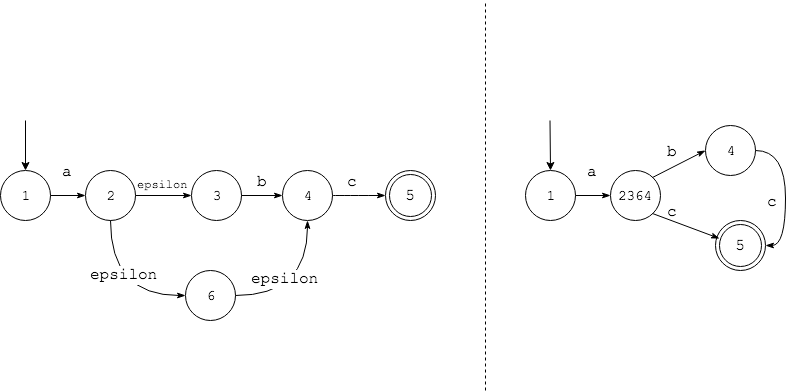
左边的NFA是对上述正则表达式的一种很直观的实现，右边是与其等价的DFA，它将所有通过epsilon所到达的状态进行了合并，解决了上述两个问题。

小结

string是一组字符的合集
每个Regular Expression对应一个DFA，反之亦然
NFA可以转化为DFA
使用fsmsim函数来实现regular expression的解析

在实际的解析过程中，我们几乎不会用到fsmsim函数，而是直接使用正则表达式，但了解其如何工作的对理解Parser很重要，接下来我们将讨论如何如何实现词法分析，将表达式切分成token

词法分析器

了解了正则表达式的计算原理，我们就可以用它来实现词法分析器。关于什么是Lexer，可以参考之前编译原理的文章，Python提供了一个Lexer的类库ply，可以方便的将句子切分成token，但有几点需要注意：

首先是匹配token的顺序和优先级，比如匹配WORD的正则式为r'[^ <>]+'，匹配string的正则式为r'"[^"]+"'，对于下字符hello "world",如果WORD的正则在前，则匹配的结果为 [WORD, WORD]，如果STRING在前，则匹配的结果为[WORD, STRING]。
另一问题是不同状态机的互斥，例如，代码注释可以穿插在代码中，对注释的解析需要令一个的状态机，和解析HTML Token的状态机互斥，例如下面的代码

 webpage = '''Welcome to <b>my <!-- careful </b> --> webpage</b>'''

当遇见<!--时，进入解析注释的状态机，并将结果排除在Token之外

HTML Lexer

这一节我们以HTML文本为例，来实现一个简单的lexer，首先我们可以根据HTML的标签规则生成一组tokens:

tokens = (
    'LANGLE', # <
    'LANGLESLASH', #</
    'RANGLE', #>
    'EQUAL', #=
    'STRING', #"hello"
    'WORD' #welcome!
)

然后对每个token，我们可以按照ply的规则给出匹配的正则式，这里特比要注意前面提到的第二点，ply默认由上到下匹配，一旦命中匹配规则，则会立即返回，不会继续向下匹配。由于篇幅原因，这里不会列出所有的token

# HTML Tokens
def t_LANGLESLASH(token):
    r'</'
    return token

def t_LANGLE(token):
    r'<'
    return token
#...

def t_newline(token):
    r'\n'
    token.lexer.lineno += 1
    pass

有了token的正则式，我们便可以用ply内部的方法，HTML代码token化：


htmllexer = lex.lex()
htmllexer.input(webpage)
while True:
    #return next token
    tok = htmllexer.token() 
    if not tok: 
        break
    print(tok)


LexToken(WORD,'This',1,0)
LexToken(WORD,'is',1,5)
LexToken(LANGLE,'<',2,26)
LexToken(WORD,'b',2,27)
LexToken(RANGLE,'>',2,28)
LexToken(WORD,'my',2,29)
LexToken(LANGLESLASH,'</',2,31)
LexToken(WORD,'b',2,33)
LexToken(RANGLE,'>',2,34)
LexToken(WORD,'webpage!',2,36)

Build a parser by hand

Resources

Programming Language