贝叶斯模型

Course Notes from Udacity Self-Driving Car Nanodegree Program

贝叶斯模型概述

在现实的生活中，我们对某事的判断往往有一个先验概率，比如今天是阴天，感觉下雨的概率是50%，这些先验概率可以来自我们的经验，也可以来自一些统计数据。但是我们都知道，经验往往是靠不住的，因此先验概率往往是不够精确的，为了得到更精确的结果，我们需要引入一些额外的信息，这些信息可以帮助我们矫正之前的先验概率，比如，天气预报说今天有雨，那么我们会觉得今天下雨的可能性增大了。换一种说法，通过引入的额外信息，我们可以重新计算出一个新的概率，称为后验概率，这个概率比先验概率更准确，这就是贝叶斯模型的大概含义。

条件概率公式

要理解贝叶斯模型，先要复习一下什么是条件概率和全概率。所谓条件概率是指在某件事发生的前提下，另一件事发生的概率。和独立概率比起来条件概率不是很好理解，因为平时生活中能直接使用上这种概率的机会比较少，一个经典条件概率实验是红蓝球实验:

一个袋子中有2颗蓝球和3颗红球，每次从袋子里拿一颗，拿完不放回，问连续两次都拿到蓝球的概率是多少？

按照上面给出的条件，在开始时袋子里一共有5球，第一次拿到红球或者蓝球的概率是独立的，即拿到红球概率为3/5，拿到蓝球的概率为2/5。当第一次拿完后，袋子里的球变成了4个，此时袋子里红篮球的比例受第一次拿球操作的影响，即如果第一次拿的是红球，那么袋子里剩下的是2个蓝球+2个红球，那么第二次拿蓝球的概率为2/4，如果第一次拿的是蓝球，那么袋子里剩下的是3个红球和1个蓝球，则第二次拿到蓝球的概率为1/4，则两次都拿到蓝球的概率为2/5 x 1/4 = 1/10

上面例子中，第二次拿球的概率受第一次拿球的结果的影响，我们可以说第二次拿到某个球的概率是一种“条件概率”。条件概率可以用文氏图来表达，例如我们想要表达在B发生的条件下A发生的概率，用文氏图可以表示如下

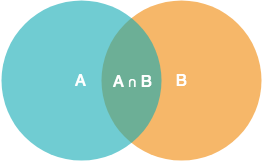
根据文氏图，可以很直观地看到在事件A发生的情况下事件B发生的概率是交集部分的概率，因此，对于条件概率也可以这么理解，我们假设事件A有N个样本，某一次事件A发生了，其中有M个样本恰好是B的样本，则条件概率为M/N，它可以认为是在A的样本中寻找B的份额占比。

如果用数学符号表达条件概率，则可以按照如下方式推导：

1. $P(A) \thinspace = N \thinspace / \thinspace 样本空间 $
2. $P(A∩B) \thinspace = M \thinspace / \thinspace 样本空间 $
3. $P(B|A) \thinspace = M/N = P(A∩B)/P(A)$

其中$P(A∩B)$表示A和B的联合概率分布也可表示为$P(A,B)$或$P(AB)$，通常这部分交集不太好寻找，但是由于$P(A∩B)$等于$P(B∩A)$，因此可以将问题转化为

这个就是条件概率公式，将AB交集部分化简掉，可以得到

条件概率有时也被称作后验概率。为了加深对条件概率的理解，我们再来看一个条件概率的例子，这个例子是说：在一个4条车道的高速路上，车有两种行驶状态，一种是高速行驶，另一种是非高速行驶，高速行驶的车必须在最左侧的车道上，现在有下面一些统计数据：

1. 任何时候行驶，有20%的车辆行驶在最左侧车道上
2. 高速上40%的车都是高速行驶的车
3. 对于行驶在最左车道上的车，有90%的车是高速行驶的

有了上述信息，现在想要知道如果一辆车是高速行驶的，那么它位于最左面车道的概率是多少？

这个问题并不难解，可直接套用上面公式，由于篇幅原因，这里略去推导过程，直接给出结果

全概率公式

为了理解贝叶斯定理，除了条件概率以外，我们还需要推倒一下全概率公式，如果理解了条件概率，那么全概率公式理解起来就相对比较简单，我们还用文氏图来表达

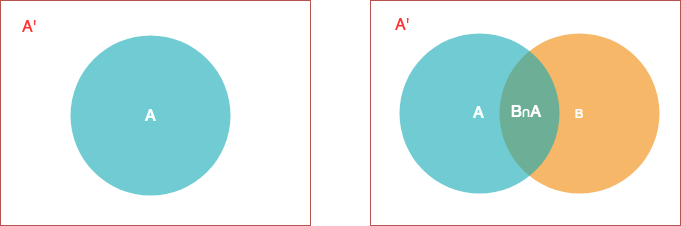
左图中，A和A'构成样本空间S，即 P(A)+P(A')=1。在这种情况下，右图中B发生的概率为B和A的交集加上B和A’的交集，即 P(B) = P(B∩A) + p(B∩A')，有前面的推导可知，P(B∩A)=P(B|A)P(A)，带入化简，得到全概率公式:

它的含义是，如果A和A'构成样本空间的一个划分，那么事件B的概率，就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。即在A发生的条件下B发生的概率加上在A没发生的条件下B发生的概率。为了加深对全概率公式的理解，我们同样给出一个例子：

1. 1%的人会的癌症
2. 在得癌症的人中，90%的癌症检测结果都是阳性
3. 在没有得癌症的人中，10%的人检测结果是假阳性（意思是这些人没有得癌症，却被误诊为癌症）

现在的问题是，如果一个人去检查癌症的结果是阳性，那么它有多大几率得癌症？

我们令换癌症的概率为P(C),检测结果为阳性的概率为P(Pos)，则有：P(C)=0.01,P(Pos|C)=0.9，P(Pos|C')=0.1；问题是求解P(C|Pos)。由条件概率公式可得

这时我们发现P(Pos)未知，因此暂时求不出来P(C|Pos)，但是这里忽略了一个条件，即P(Pos|C')=0.1没有用上，参考上面全概率公式，我们可以按照如下式子求解P(Pos)

将该值代入到上式，可得

贝叶斯定理

有了前面的铺垫，我们可以先给出贝叶斯公式，然后再讨论其含义，将上面条件概率变形得到：

其中P(A)称为”先验概率”（Prior probability），即在B事件发生之前，我们对A事件概率的一个判断。P(A|B)称为”后验概率”（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。P(B|A)/P(B)称为”可能性函数”（Likelyhood），这是一个调整因子，使得预估概率更接近真实概率。所以，条件概率可以理解成下面的式子：

这就是贝叶斯推断的含义。我们先预估一个”先验概率”，然后加入实验结果，看这个实验到底是增强还是削弱了”先验概率”，由此得到更接近事实的”后验概率”。如果”可能性函数P(B|A)/P(B)>1，意味着”先验概率”被增强，事件A的发生的可能性变大；如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；如果"可能性函数"<1，意味着”先验概率”被削弱，事件A的可能性变小。

我们还是用一个例子来加深一下对贝叶斯定理的理解，只不过这次不需要计算，例子还是上面计算癌症概率的问题，对于上述例子中。我们先有了一个患癌症的先验概率P(C)=0.01，由于这个数据包含着一定的误差，为了矫正这个误差我们引入了癌症测试，即我们需要统计所有癌症测试为阳性的癌症概率，而这个结果就是我们希望得到的后验概率P(C|Pos)，理论上它要比先验概率更精确，于是将上个例子中的公式修改一下，可以得到下面的式子

贝叶斯定理也可以用来计算多个事件，比如有一个机器人，它在位于ABC三个区域内的概率均为1/3，如下所示，现在有如下数据

1. $P(R|A)=0.9$ , 在A区域看到红色的概率为0.9
2. $P(G|B)=0.9$ , 在B区域看到绿色的概率为0.9
3. $P(G|C)=0.9$ , 在C区域看到绿色的概率为0.9

求解如果机器人看到的是红色，那么它位于A,B,C三个区域的概率各自是多少？

首先我们还是有一个先验概率1/3，即机器人在每个区域内的概率均为0.333，接下来我们来计算调整因子，这次的计算方式和上面稍有不同，我们先计算三个区域的联合概率并求和，然后再分别计算各自的条件概率

1. $P(A∩R) \thinspace = \thinspace P(R|A) \times P(A) \thinspace = \thinspace 0.9 \times 0.3 \thinspace = \thinspace 0.3 $
2. $P(B∩R) \thinspace = \thinspace P(R|B) \times P(A) \thinspace = \thinspace (1-0.9) \times 0.3 \thinspace = \thinspace 0.033 $
3. $P(C∩R) \thinspace = \thinspace P(R|A) \times P(A) \thinspace = \thinspace (1-0.9) \times 0.3 \thinspace = \thinspace 0.033 $

有了上面联合概率分布，就可以计算机器人处在任何位置看见红色的概率

和前面计算不同的是，这里计算$P(R)$并没有直接套用全概率公式，而是分步进行的（如果将上面式子展开成全概率公式，则非常复杂），有了$P(R)$就可以直接计算各自的条件概率

1. $P(A|R) \thinspace = \thinspace \frac {P(R∩A)}{P(R)} \thinspace = \thinspace \frac{0.3}{0.56} \thinspace = \thinspace 0.818 $
2. $P(B|R) \thinspace = \thinspace \frac {P(B∩A)}{P(R)} \thinspace = \thinspace \frac{0.033}{0.56} \thinspace = \thinspace 0.091 $
3. $P(C|R) \thinspace = \thinspace \frac {P(C∩A)}{P(R)} \thinspace = \thinspace \frac{0.033}{0.56} \thinspace = \thinspace 0.091 $

从这个例子，我们更可以看出，所谓计算贝叶斯概率或者是条件概率都是在求解一个比值，这个比值为"两个事件联合概率/某个事件单独发生的概率"。而从结果上看，我们通过引入其他信息（机器人识别颜色的概率）重新校准了先验概率，使后面的预测更加准确。

至此，我们可以先总结一下贝叶斯公式的计算步骤：

1. 得到某件事情发生的先验概率 $P(H)$，进而的到 $P(H’)$
2. 根据已有的先验信息，进行某种试验$T$，观察试验结果，得到条件概率： $P(T|H)$ 以及 $P(T|H’)$ , 进而得到 $P(T’|H) = 1-P(T|H) $
3. 计算先验概率和试验概率的联合概率：
   • $ P(T,H) = P(T|H)*P(H) $
   • $ P(T,H’) = P(T|H’)*P(H’) $
4. 计算试验结果出现的概率，即全概率: $P(T) = P(T,H) + P(T,H’)$
5. 计算贝叶斯概率，即通过试验矫正后的概率：$P(H|T) = \frac {P(T|H)*P(H)}{P(T)} $

自动驾驶中的贝叶斯模型

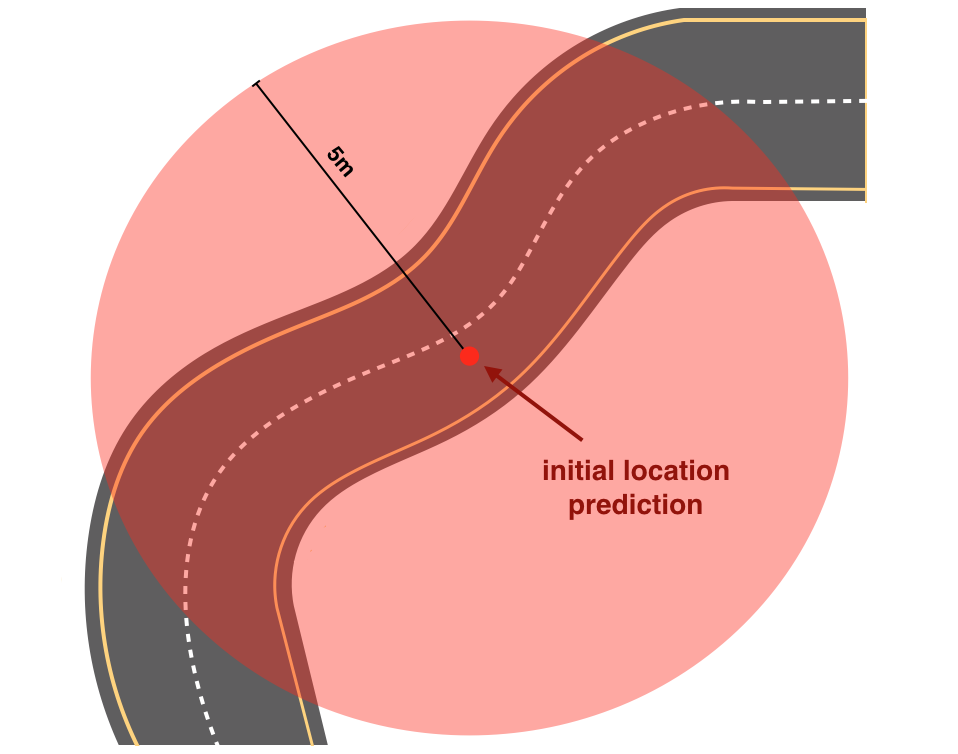
贝叶斯定理在自动驾驶领域应用非常广泛也非常重要，我们可以通过某种先验信息-比如GPS定位，先得到车的一个初步位置，通常来说这个初步位置和真实位置有5m左右的误差(GPS误差)，如下图左边所示

显然，5m的误差对于行驶在路上的汽车来说是不可接受的，因此我们还需要通过车各种传感器收集更多的收据来矫正车的位置，常用外部传感器有

1. Carmera，采集图像
2. Lidar，360度激光测距
3. Radar，360度雷达扫描

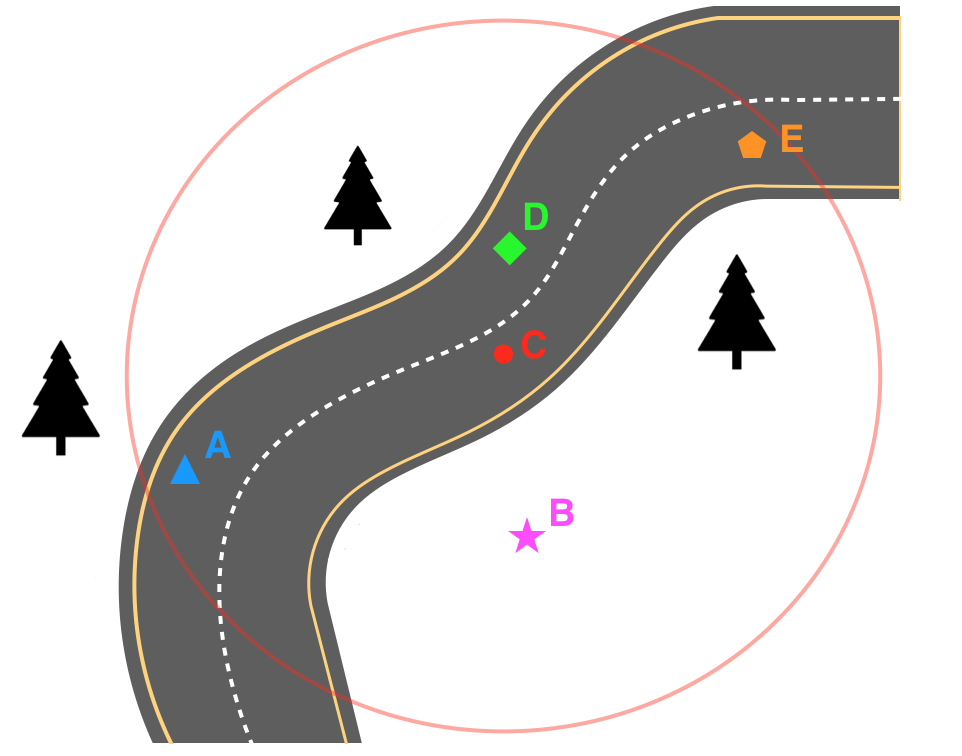
除了外部传感器，车内部传感器也会收集车当前的状态信息，比如车速，朝向，车轮朝向等。现在假设有一辆车，通过GPS定位的位置在C（如右图所示）通过这些传感器收集到的信息有：

1. 车正在上坡
2. 车左边有一棵树
3. 车轮指向右边

我们可以通过这些数据来重新矫正车的位置（虽然现在还不知道该如何矫正，但是可以获得一些感性的认识），上面的例子中，矫正之后的点是A点。在下一篇文章中，我们将会详细分析机器人的定位原理。

（全文完）

Resources

• Udacity Intro to Self-Driving Car
• 贝叶斯定理Wiki
• 贝叶斯推断及其互联网应用（一）：定理简介

附录

Solution code for project Joy Ride:

car_parameters = {"throttle": 0, "steer": 0, "brake": 0}

def control(pos_x, pos_y, time, velocity):
    """ Controls the simulated car"""
    global car_parameters
    if(time < 3):
        car_parameters["throttle"] = -1.0
        car_parameters["steer"] = 1
        car_parameters["brake"] = 0
    elif(pos_y > 32):
        car_parameters["throttle"] = -1.0
        car_parameters["steer"] = -1
        car_parameters["brake"] = 0
    else:
        car_parameters["throttle"] = 0
        car_parameters["steer"] = 0
        car_parameters["brake"] = 1
    
    return car_parameters
    
import src.simulate as sim
sim.run(control)

• Code simulation on Youtube