神经网络

Posted on 2017-10-05 | In Machine Learning , AI

文中所用到的图片部分截取自Andrew Ng在Cousera上的课程

逻辑回归的问题

神经网络目前是一个很火的概念，在机器学习领域目前还是主流，之前已经介绍了线性回归和逻辑回归，为什么还要学习神经网络？以non-linear classification为例，如下图所示

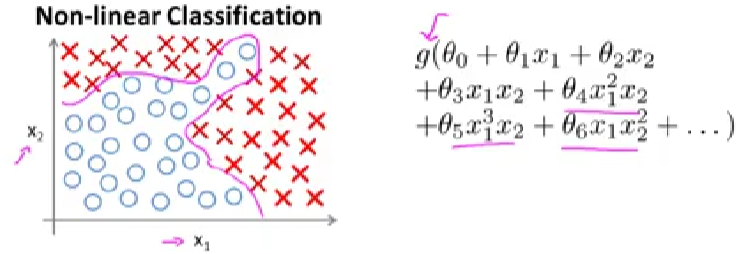
我们可以通过构建对feature的多项式$g_\theta$来确定预测函数，但这中方法适用于feature较少的情况，比如上图中，只有两个feature: $x_1$和$x_2$。

当feature多的时候，产生多项式就会变得很麻烦，还是预测房价的例子，可能的feature有很多，比如：x1=size,x2=#bedrooms,x3=#floors,x4=age,…x100=#schools等等，假设n=100，有几种做法：

构建二阶多项式
- 如$x_1^{2}$,$2x_1$,$3x_1$,…,$x_2^{2}$,$3x_2$…有约为5000项(n^2/2)，计算的代价非常高。
- 取一个子集，比如x1^2, x2^2,x3^2...x100^2，这样就只有100个feature，但是100个feature会导致结果误差很高
构建三阶多项式
- 如x1x2x3, x1^2x2, x1^2x3...x10x11x17..., 有约为n^3量级的组合情况，约为170,000个

另一个例子是图像识别与分类，例如识别一辆汽车，对于图像来说，是通过对像素值进行学习（车共有的像素特征vs非汽车特征），那么feature就是图片的像素值，如下图所示，假如有两个像素点是车图片都有的：

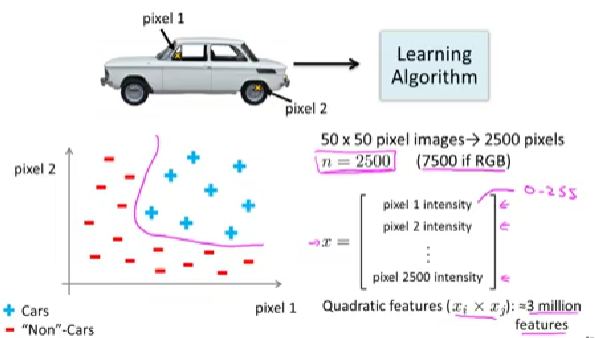
假设图片大小为50x50，总共2500个像素点，即2500个feature（灰度图像，RGB乘以三），如果使用二次方程，那么有接近300万个feature，显然图像这种场景使用non linear regression不合适，需要探索新的学习方式

单层神经网络

所谓神经元(Neuron)就是一种计算单元，它的输入是一组特征信息$x_1$…$x_n$，输出为预测函数的结果。

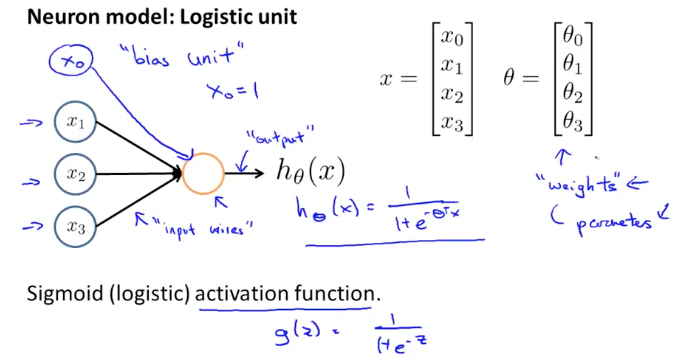
如上图，是一个单层的神经网络，其中：

输入端$x_0$默认为1，也叫做”bias unit.”
$\theta$矩阵在神经网络里也被叫做权重weight矩阵

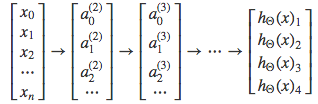
对于上述单层神经网络的输出函数$h_\theta(x)$，可以表示为

\[h_\theta(x) = g(\theta^Tx) = g(\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_4)\]

其中，$\theta_0$为bias uint，g为sigmoid函数$\frac{1}{1+e^{-z}}$，作用是将输出的值映射到[0,1]之间。因此最终的输出函数也可以写作

\[h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\]

公式有些抽象，我们看看如何用Pytorch来实现

import torch

def activation(x):
    return 1 / (1+torch.exp(-x))

## Generate some data
torch.manual_seed(7) #set the random seed so things are predictable

## Features are 5 random normal variables
features = torch.randn((1,5)) #1x5

# True weights for our data, random normal variables again
# same shape as features
weights = torch.randn_like(features) #1x5

#and a true bias term
bias = torch.randn((1,1))

# weights.view will convert the matrix to 5x1
# torch.mm does the matrxi multiplication
y = activation(bias + torch.mm(features, weights.view(5,1)))

多层神经网络

上述的神经网络只有输出端一个Neuron，属于比较简单的神经网络，我们再来看一个多个Neuron的两层神经网络，如下图所示

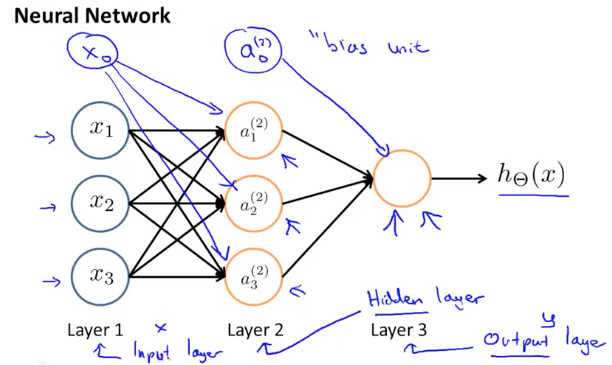
上述神经网络中的第一层是叫”Input Layer”，最后一层叫”Output Layer”，中间叫”Hidden Layer”，用$a_0^2…a_n^2$表示，他们也叫做”activation units.” 其中

输入层的$x_i$为样本feature，$x_0$作为”bias”
中间层的$a_i^{(j)}$ 表示第j层的第i个节点，我们可以加入$a_0^{(2)}$作为”bias unit”，也可以忽略

\[\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} \to \begin{bmatrix} a_1^{(2)} \\ a_2^{(2)} \\ a_3^{(2)} \\ \end{bmatrix} \to h_\theta(x)\]

对第二层每个activation节点的计算公式如下：

\[a_1^{(2)} = g(\theta_{10}^{(1)}x_0 + \theta_{11}^{(1)}x_1 + \theta_{12}^{(1)}x_2 + \theta_{13}^{(1)}x_3 ) \\ a_2^{(2)} = g(\theta_{20}^{(1)}x_0 + \theta_{21}^{(1)}x_1 + \theta_{22}^{(1)}x_2 + \theta_{23}^{(1)}x_3 ) \\ a_3^{(2)} = g(\theta_{30}^{(1)}x_0 + \theta_{31}^{(1)}x_1 + \theta_{32}^{(1)}x_2 + \theta_{33}^{(1)}x_3 ) \\ h_\theta(x) = a_1^{(3)} = g(\theta_{10}^{(2)}a_0^{2}+\theta_{11}^{(2)}a_1^{2}+\theta_{12}^{(2)}a_2^{2}+\theta_{13}^{(2)}a_3^{2})\]

上面可以看到第一层Hidden Layer的参数，$\theta_{ij}$表示从节点i到节点j的权重值，$\theta^{(l)}$表示该权重位于第l层。如果单独看每一个a节点的值，会发现它和上述单层神经网络的计算方式一样，需要一个bias unit和$\theta$权重。如上图中的$\theta$矩阵是3x4的，输入的feature矩阵是4x1的，这样相乘得出的第一层输出矩阵是3x1的，对应每个a节点的值。而整个神经网络最终输出结果是神经元a矩阵再乘以第二层Hidden Layer的参数矩阵$\theta^{(2)}$。由此我们可以推测出$\theta$矩阵的维度的计算方式为:

如果神经网络第j层有$m$个单元，第j+1层有$n$个单元，那么$\Theta$矩阵的维度为$n \times (m+1)$

以上面的例子来说, 如果layer1有两个三个输入节点，即$m=3$, layer2 有三个activation节点，即$n=3$。那么$\Theta$矩阵是3x4的。为什么要+1呢？原因是在输入层(input layer)要引入$x_0$作为bias, 对应

为了简化上面Hidden Layer的式子，我们定义一个新的变量$z_k^{(j)}$来表示g函数的参数，则上述节点a的值可表示如下：

\[a_1^{(2)} = g(z_1^{(2)}) \\ a_2^{(2)} = g(z_2^{(2)}) \\ a_3^{(2)} = g(z_3^{(2)}) \\ a_1^{(3)} = g(z_3^{(2)})\]

和前面一样，上脚标用来表示第几层layer，下脚标用来表示该layer的第几个节点。例如j=2时的第k个节点的值为

\[a_k^{(2)} = g(z_k^{(2)}) \\ z_k^{(1)} = \theta_{k0}^{(1)}x_0 + \theta_{k1}^{(1)}x_1 + ... + \theta_{kn}^{(1)}x_n\]

将上面式子做进一步推导并用向量表示为

\[a^{(j)} = g(z^{(j-1)}) \\ z^{(j-1)} = \theta^{(j-1)}a^{(j-1)}\]

我们用结合上面的三层神经网络来简单验证下，假设j=3那么第三层神经网络节点的值$z^{(3)}$为

\[z^{(3)} = \theta^{(2)}a^{(2)} h_\theta(x) = a^{(3)} = g(z)\]

其中，上角标用来表示第几层layer，下角标表示该层的第几个节点。例如第2层的第k个节点的z值为：

\[z_k^{(2)} =\]

z_{k}^{(2)} = Θ_{k, 0}^{(1)} x_{0} + Θ_{k, 1}^{(1)} x_{1} + \dots + Θ_{k, n}^{(1)} x_{n}

用向量表示x和 $z^{j}$ 如下：

\begin{aligned} x = [\begin{matrix} x_{0} \\ x_{1} \\ \dots \\ x_{n} \end{matrix}] & z^{(j)} = [\begin{matrix} z_{1}^{(j)} \\ z_{2}^{(j)} \\ \dots \\ z_{n}^{(j)} \end{matrix}] \end{aligned}

令x为第一层节点 $x = a^{(1)}$ ，则每层的向量化表示为：

z^{(j)} = Θ^{(j - 1)} a^{(j - 1)}

其中， $Θ^{(j-1)}$ 是 jx(j+1) 的， $a^{(j-1)}$ 是(j+1)x1的，因此 $z^{j}$ 是jx1的，即

a^{(j)} = g (z^{(j)})

当我们计算完 $a^{(j)}$ 后，我们可以给 $a^{(j)}$ 增加一个bias unit，即 $a_{0}^{(j)} = 1$ ，则a变成了(j+1)x1的。以此类推：

z^{(j + 1)} = Θ^{(j)} a^{(j)}

最终的预测函数h表示为：

h_{Θ} (x) = a^{(j + 1)} = g (z^{(j + 1)})

注意到在每层的计算上，我们的预测函数和逻辑回归基本相同。我们增加了这么多层，即神经网络是为了更好的得到非线性函数的预测结果，这个算法也叫做Forward Propagation，后面简称FB算法，Octave实现为：

function g = sigmoid(z)
	g = 1.0 ./ (1.0 + exp(-z));
end

function p = predict(Theta1, Theta2, X)

m = size(X, 1);
num_labels = size(Theta2, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

a1 = [ones(m, 1), X];
a2 = sigmoid(a1*Theta1');
a2 = [ones(m,1) a2];
h = sigmoid(a2*Theta2');

% Hint: The max function might come in useful. In particular, the max
%       function can also return the index of the max element, for more
%       information see 'help max'. If your examples are in rows, then, you
%       can use max(A, [], 2) to obtain the max for each row.
%
[max,index] = max(h,[],2);
p = index;

end

Neural Network Example

单层神经网络实现与或门

神经网络的一个简单应用是预测 $x_{1}$ AND $x_{2}$ ，当 $x_{1}$ 和 $x_{2}$ 都为1的时候，结果是true，预测函数如下：

\begin{aligned} [\begin{matrix} x_{0} \\ x_{1} \\ x_{2} \end{matrix}] \to [\begin{matrix} g (z^{(2)}) \end{matrix}] \to h_{Θ} (x) \end{aligned}

x_{0}

为1，我们假设 $θ^{(1)}$ 的值如下： $Θ^{(1)} = [\begin{matrix} - 30 & 20 & 20 \end{matrix}]$

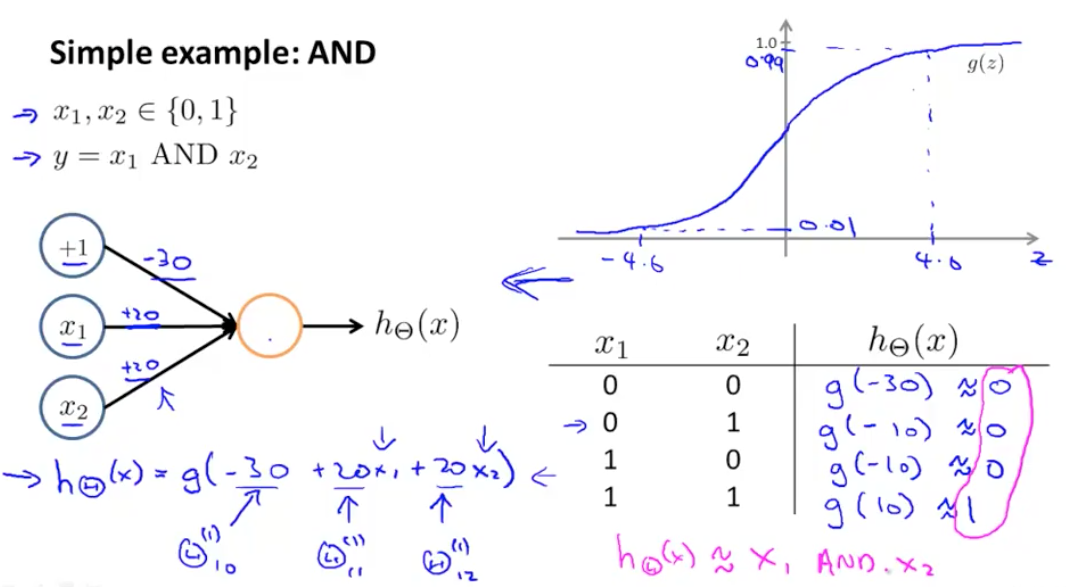
如图所示，我们构建了一个一层的神经网络来处理计算机的”AND”请求，来代替原来的“与门”。神经网络可用来构建所有的逻辑门，比如”OR”运算如下图：

二级神经网络构建同或门

上面我们实现了与或非(非的推导忽略)，对应的theta矩阵如下：

</br>

\begin{aligned} A N D : \\ Θ^{(1)} & = [\begin{matrix} - 30 & 20 & 20 \end{matrix}] \\ N O R : \\ Θ^{(1)} & = [\begin{matrix} 10 & - 20 & - 20 \end{matrix}] \\ O R : \\ Θ^{(1)} & = [\begin{matrix} - 10 & 20 & 20 \end{matrix}] \end{aligned}

我们可以通过上面的矩阵来构建XNOR门：

\begin{aligned} [\begin{matrix} x_{0} \\ x_{1} \\ x_{2} \end{matrix}] \to [\begin{matrix} a_{1}^{(2)} \\ a_{2}^{(2)} \end{matrix}] \to [\begin{matrix} a^{(3)} \end{matrix}] \to h_{Θ} (x) \end{aligned}

第一层节点的θ矩阵为：

Θ^{(1)} = [\begin{matrix} - 30 & 20 & 20 \\ 10 & - 20 & - 20 \end{matrix}]

第二层节点的θ矩阵为:

Θ^{(2)} = [\begin{matrix} - 10 & 20 & 20 \end{matrix}]

每层节点的计算用向量化表示为：

\begin{aligned} a^{(2)} = g (Θ^{(1)} \cdot x) \\ a^{(3)} = g (Θ^{(2)} \cdot a^{(2)}) \\ h_{Θ} (x) = a^{(3)} \end{aligned}

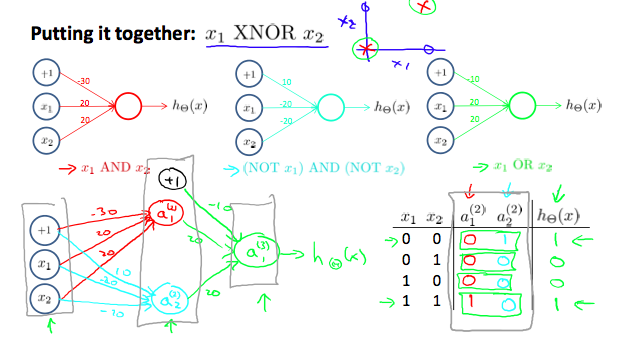
Multiclass Classification

使用神经网络进行多种类型分类的问题，我们假设最后的输出是一个向量，如下图所示

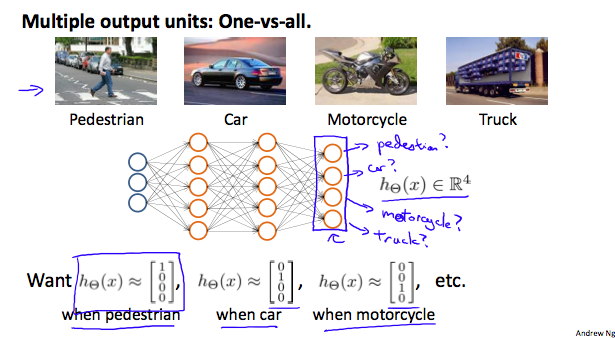
上面的例子中，对于输出结果y的可能情况有：

每一个 $y^{(i)}$ 向量代表一中分类结果，抽象来看，多级神经网络分类可如下表示：

Cost Function

先定义一些变量:
- L = 神经网络的层数
- $S_{l}$
  = 第l层的节点数
- K = 输出层的节点数，即输出结果的种类。
  - 对0和1的场景，K=1， $S_{l} = 1$
  - 对于多种分类的场景，K>=3， $S_{l} = K$
  - 用 $h_{Θ} (x)_{k}$ 表示第K个分类的计算结果
Cost Function

参考之前的逻辑回归cost函数：

J (θ) = - \frac{1}{m} \sum_{i = 1}^{m} [y^{(i)} \log (h_{θ} (x^{(i)})) + (1 - y^{(i)}) \log (1 - h_{θ} (x^{(i)}))] + \frac{λ}{2 m} \sum_{j = 1}^{n} θ_{j}^{2}

对神经网络来说，输出结果不再只有两种类型，而是有K种分类，cost函数也更加抽象和复杂：

\begin{matrix} J (Θ) = - \frac{1}{m} \sum_{i = 1}^{m} \sum_{k = 1}^{K} [y_{k}^{(i)} \log ((h_{Θ} (x^{(i)}))_{k}) + (1 - y_{k}^{(i)}) \log (1 - (h_{Θ} (x^{(i)}))_{k})] + \frac{λ}{2 m} \sum_{l = 1}^{L - 1} \sum_{i = 1}^{s_{l}} \sum_{j = 1}^{s_{l + 1}} (Θ_{j, i}^{(l)})^{2} \end{matrix}

为了计算多个输出结果，括号前的求和表示对K层分别进行计算后再累加计算结果。中括号后面是regularization项，是每层θ矩阵元素的平方和累加，公式里各层θ矩阵的列数等同于对应层的节点数，行数等它对应层的节点数+1，其中 $\sum_{i = 1}^{s_{l}} \sum_{j = 1}^{s_{l + 1}} (Θ_{j, i}^{(l)})^{2}$ 是每个θ矩阵项的平方和， $\sum_{l = 1}^{L - 1}$ 代表各个层θ矩阵的平方和累加。理解了这两部分就不难理解regularization项了，它和之前逻辑回归的regularization项概念是一致的。

理解上述式子着重记住以下三点：

前两个求和符号是对每层神经网络节点进行逻辑回归cost function运算后求和
后面三个求和符号是是每层神经网络节点的θ矩阵平方和的累加求和
特殊注意的是，后面三个求和符号中第一个求和符号中的i代表层数的index，不代表训练样本的index

Octave demo

假设有三层神经网络，已知权重矩阵Theta1，Theta2，代价函数使用代数形式描述为：

function [J grad] = nnCostFunction(num_labels,X, y, Theta1, Theta2, lambda)

% X:5000x400
% y:5000x1
% num_labels:10
% Theta1: 25x401
% Theta2: 10x26

% Setup some useful variables
m = size(X, 1);
J = 0;


% make Y: 5000x10
I = eye(num_labels);
Y = zeros(m, num_labels);
for i=1:m
  Y(i, :)= I(y(i), :);
end

% cost function
J = (1/m)*sum(sum((-Y).*log(h) - (1-Y).*log(1-h), 2));
% regularization item
r = (lambda/(2*m))*(sum(sum(Theta1(:, 2:end).^2, 2)) + sum(sum(Theta2(:,2:end).^2, 2)));

% add r
J = J+r;

end

Backpropagation algotrithm

“Backpropagation”是神经网络用来求解Cost Function最小值的算法，类似之前线性回归和逻辑回归中的梯度下降法。上一节我们已经了解了Cost Function的定义，我们的目标是求解：

min_{Θ} J (Θ)

即找到合适的θ值使Cost Function的值最小，即通过一个合适的算法来求解对θ的偏导

\frac{\partial}{\partial Θ_{i, j}^{(l)}} J (Θ)

我们先假设神经网络只有一个训练样本(x,y)，我们使用“Forward Propagation”的向量化方式来逐层计算求解出最后的结果

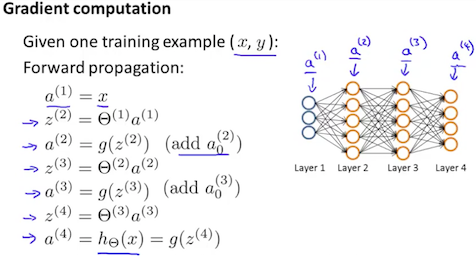
接下来我们要求θ矩阵的值，用到的算法叫做“Backpropagation”，我们定义：

δ_{j}^{(l)} = "error" of node j in layer l

假设 Layer L=4 那么有：

δ_{j}^{(4)} = a_{j}^{(4)} - y_{j}

向量化表示为：

δ^{(4)} = a^{(4)} - y

其中，δ，a，y向量行数等于最后一层节点的个数，这样我们首先得到了最后一层的δ值，接下来我们要根据最后一层的δ值来向前计算前面各层的δ值，第三层的公式如下：

δ^{(3)} = ((Θ^{(3)})^{T} δ^{(4)}) . * g^{'} (z^{(3)})

第二层的计算公式如下：

δ^{(2)} = ((Θ^{(2)})^{T} δ^{(3)}) . * g^{'} (z^{(2)})

</br> 第一层是输入层，是样本数据，没有错误，因此不存在 $δ^{(1)}$
</br>

在上述的式子中， $g^{'}$ 对 $z^{(l)}$ 的求导等价于下面式子：

g^{'} (z^{(l)}) = a^{(l)} . * (1 - a^{(l)})

因此我们可以看到所谓的Backpropagation Algorithm即是先计算最后一层的δ值，然后依次向前计算各层的δ值。

如果忽略regularization项，即 $λ = 0$ ，我们能够发现如下式子:

\frac{\partial}{\partial Θ_{i, j}^{(l)}} J (Θ) = a_{j}^{(l)} δ_{i}^{(l+1)}

上面是Layer L=4的例子，让我们对Backpropagation Algorithm先有了一个直观的感受，接下来从通用的角度给出Backpropagation Algorithm的计算步骤

假设有训练集 ${(x^{(1)}, y^{(1)}) \dots (x^{(m)}, y^{(m)})}$ ，令

对所有 $i, j, l$ ，令 $Δ_{i, j}^{(l)}$ = 0，得到一个全零矩阵
For i=1 to m 做循环，每个循环体执行下面操作
1. $a^{(1)} := x^{(t)}$
  让神经网络第一层等于输入的训练数据
2. 对 $a^{(l)}$ 进行“Forward Propagation”计算，其中 l=2,3,…,L 计算过程如上文图示
3. 使用 $y^{(t)}$ 来计算 $δ^{(L)} = a^{(L)} - y^{(t)}$
4. 根据 $δ^{(L)}$ 向前计算 $δ^{(L - 1)}, δ^{(L - 2)}, \dots, δ^{(2)}$ ，公式为： $δ^{(l)} = ((Θ^{(l)})^{T} δ^{(l + 1)}) . * a^{(l)} . * (1 - a^{(l)})$ 这个过程涉及到了链式法则，在下一节会介绍
5. $Δ_{i, j}^{(l)} := Δ_{i, j}^{(l)} + a_{j}^{(l)} δ_{i}^{(l + 1)}$
  对每层的θ矩阵偏导不断叠加，进行梯度下降，前面的式子也可以用向量化表示 $Δ^{(l)} := Δ^{(l)} + δ^{(l + 1)} (a^{(l)})^{T}$
加上Regularization项得到最终的θ矩阵
- 当 j≠0 时，$ D_{i,j}^{(l)} \thinspace := \thinspace \frac{1}{m}(\Delta_{i,j}^{(l)} + \lambda \Theta_{i,j}^{(l)}), \thinspace if \thinspace $
- 当 j=0 时，$ D_{i,j}^{(l)} \thinspace := \thinspace \frac{1}{m}\Delta_{i,j}^{(l)} $

大写的D矩阵用来表示θ矩阵的计算是不断叠加的，我们最终得到的偏导式子为：

\[\frac{\partial{J(\Theta)}}{\partial\Theta_{ij}^{(l)}} \thinspace = \thinspace D_{(ij)}^{(l)}\]

Backpropagation Intuition

这一小节对上面提到的Backpropagation(后面简称BP算法)做一个简单的数学推到，来搞清楚 $δ_{j}^{(l)}$ 的计算过程。

还是先看Forward Propagation，我们还是拿前面的图距离，假设神经网络如下图

他只有一个输出节点，由之前提到的Forward Propagation得到的预测函数为：

h_{Θ} (x) = a_{1}^{(3)} = g (Θ_{10}^{(2)} a_{0}^{(2)} + Θ_{11}^{(2)} a_{1}^{(2)} + Θ_{12}^{(2)} a_{2}^{(2)} + Θ_{13}^{(2)} a_{3}^{(2)})

这个函数中：

$h_{Θ} (x)$
是以Θ为变量的函数
它的计算过程是从第一层开始向最后一层逐层计算，每一层每个节点的值是由它后一层的节点乘以权重矩阵Θ

BP的计算和推导不如Forward容易理解，也不直观，它的特点类和FB类似

δ也是自变量为θ的函数
它的计算过程是从最后一层开始向第一层逐层计算，每层的δ值是由它前面一层的δ值乘以权重矩阵θ
它的计算包含两部分，第一部分是求梯度（对θ求偏导），第二部分是梯度下降

先说第一部分求梯度，由上节给出的代价函数为：

\begin{matrix} J (Θ) = - \frac{1}{m} \sum_{i = 1}^{m} \sum_{k = 1}^{K} [y_{k}^{(i)} \log (h_{Θ} (x^{(i)}))_{k} + (1 - y_{k}^{(i)}) \log (1 - h_{Θ} (x^{(i)})_{k})] + \frac{λ}{2 m} \sum_{l = 1}^{L - 1} \sum_{i = 1}^{s_{l}} \sum_{j = 1}^{s_{l} + 1} (Θ_{j, i}^{(l)})^{2} \end{matrix}

如果将regularization项忽略，令K=1,对于单一节点 $x^{(i)}$ , $y^{(i)}$ 的代价函数简化为：

J (Θ) = - y^{(i)} \log (h_{Θ} (x^{(i)})) + (1 - y^{(i)}) \log (1 - h_{Θ} (x^{(i)}))

上面函数近似约等于:

J (Θ) \approx (h_{Θ} (x^{(i)}) - y^{(i)})^{2}

其中l代表神经网络layer的index，回忆这个函数的含义是计算样本 $(x^{(i)}, y^{(i)})$ 和预测结果的误差值，接下来的任务就是找到使这个函数的达到最小值的Θ，找到的办法是通过梯度下降的方式，使 $J(Θ)$ 沿梯度下降最快的方向达到极值（注意： $J(Θ)$ 不是convex函数，不一定有最小值，很可能收敛到了极值点），梯度下降需要用到 $\partial J(Θ) / \partial Θ_{j i}^{(l)}$ ，并将计算结果保存到 $Δ^{(l)}$ 中。

下面我们以3层神经网络为例，分解这个推导过程，神经网络如下图所示

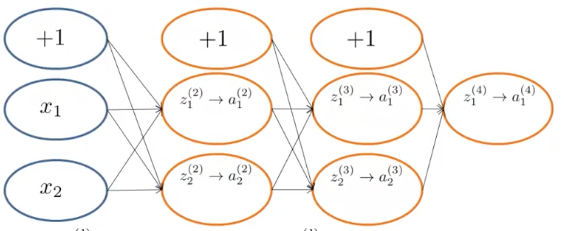
再来回顾一下各个变量的含义为：

另 $x_{1}$ 和 $x_{2}$ 表示神经网络的输入样本，两个特征
另 $z_{j}^{(l)}$ 表示第l层的第j个节点的输入值
另 $a_{j}^{(l)}$ 表示第l层的第j个节点的输出值
另 $Θ_{j i}^{(l)}$ 表示第l层到第l+1层的权重矩阵
另 $δ_{j}^{(l)}$ 表示第l层第j个节点的预测偏差值，他的数学定义为 $δ_{j}^{(l)} = \frac{\partial}{\partial z_{j}^{(l)}} J (Θ)$

我们的目的是求解Θ矩阵的值，以得出最终的预测函数，这个例子中以求解 $Θ_{11}^{(3)}$ 和 $Θ_{11}^{(2)}$ 为例

参考上面几节，我们令 $h_{Θ} (x^{(t)}) = g (z^{(t)}) = a^{(t)}$ ，其中 $g$ 为sigmoid函数 $g (z) = \frac{1}{1 + e^{- z}}$
先求 $Θ_{11}^{(3)}$ ，由链式规则，可以做如下运算： $\frac{\partial J (Θ)}{\partial Θ_{11}^{(3)}} = \frac{\partial J (Θ)}{\partial a_{1}^{(4)}} * \frac{\partial a_{1}^{(4)}}{\partial z_{1}^{(4)}} * \frac{\partial z_{1}^{(4)}}{\partial Θ_{11}^{(3)}}$
参考上面δ的定义，可知上面等式后两项为： $δ_{1}^{(4)} = \frac{\partial J (Θ)}{\partial a_{1}^{(4)}} * \frac{\partial a_{1}^{(4)}}{\partial z_{1}^{(4)}}$ ，即输出层第一个节点的误差值，展开计算如下：
$δ_{1}^{(4)} = \frac{\partial J (Θ)}{\partial a_{1}^{(4)}} * \frac{\partial a_{1}^{(4)}}{\partial z_{1}^{(4)}} = - [y * (1 - g (z)) + (y - 1) * g (z)] = - [y * (1 - g (z)) + (y - 1) * g (z)] = g (z) - y = a^{(4)} - y$
，其中用到了sigmoid函数一个特性： $g' (z) = g (z) * (1 - g (z))$
这样我们得到了 $δ_{1}^{(4)}$ （参考上一节BP算法的步骤(3)），接下来继续求解 $\frac{\partial J (Θ)}{\partial Θ_{11}^{(3)}}$ ，前面第二步等号后的最有一项 $\frac{\partial z_{1}^{(4)}}{\partial Θ_{11}^{(3)}}$ ，将 $z_{1}^{(4)}$ 展开有： $z_{1}^{(4)} = Θ_{10}^{(3)} * a_{0}^{(3)} + Θ_{11}^{(3)} * a_{1}^{(3)} + Θ_{12}^{(3)} * a_{2}^{(3)}$ ，对 $Θ_{11}^{(3)}$ 求偏导的结果为 $a_{1}^{(3)}$
将第4步与第三步的式子合并，即得出 $\frac{\partial J (Θ)}{\partial Θ_{11}^{(3)}} = δ_{1}^{(4)} * a_{1}^{(3)}$ 与上一节BP算法步骤(5)一致
接下来计算 $Θ_{11}^{(2)}$ ，链式规则可做如下运算 $\frac{\partial J (Θ)}{\partial Θ_{11}^{(2)}} = \frac{\partial J (Θ)}{\partial a_{1}^{(4)}} * \frac{\partial a_{1}^{(4)}}{\partial z_{1}^{(4)}} * \frac{\partial z_{1}^{(4)}}{\partial a_{1}^{(3)}} * \frac{\partial a_{1}^{(3)}}{\partial z_{1}^{(3)}} * \frac{\partial z_{1}^{(3)}}{\partial Θ_{11}^{(2)}}$
参考上面δ的定义，可知 $δ_{1}^{(3)} = \frac{\partial J (Θ)}{\partial a_{1}^{(4)}} * \frac{\partial a_{1}^{(4)}}{\partial z_{1}^{(4)}} * \frac{\partial z_{1}^{(4)}}{\partial a_{1}^{(3)}} * \frac{\partial a_{1}^{(3)}}{\partial z_{1}^{(3)}}$ ，由上面的步骤3可知，等式的前两项为 $δ_{1}^{(4)}$ 。这里可以看出对δ值的计算和之前的FB算法类似，如果将神经网络反向来看，当前层的 $δ^{1}$ 值是根据后一层的 $δ^{(1-1)}$ 计算得来。等式的第三项，将 $z_{1}^{(4)}$ 展开后对 $a_{1}^{(3)}$ 求导后得到 $Θ_{11}^{(3)}$ ，等式最后一项为 $g' (z_{1}^{(3)})$
将上一步的结果进行整理得到: $δ_{1}^{(3)} = δ_{1}^{(4)} * Θ_{11}^{(3)} * g' (z_{1}^{(3)})$ 和上一节BP算步骤(4)一致
将8的结果带入第6步，可得出 $\frac{\partial J (Θ)}{\partial Θ_{11}^{(2)}} = δ_{1}^{(3)} * \frac{\partial z_{1}^{(3)}}{\partial Θ_{11}^{(2)}}$ ，将 $z_{1}^{(3)}$ 展开后对 $Θ_{11}^{(2)}$ 求导得到 $a_{1}^{(2)}$
整理第9步结果可知 $\frac{\partial J (Θ)}{\partial Θ_{11}^{(2)}} = δ_{1}^{(3)} * a_{1}^{(2)}$ ，与上一节步骤（5）一致

通过上面的推导，大概可以印证上一节的结论：

\frac{\partial}{\partial Θ_{i, j}^{(l)}} J (Θ) = a_{j}^{(l)} δ_{i}^{(l+1)}

而关于对 $δ_{j}^{(l)}$ 的计算则是BP算法的核心，继续上面的例子，计算 $δ_{2}^{(3)}$ 和 $δ_{2}^{(2)}$ ：

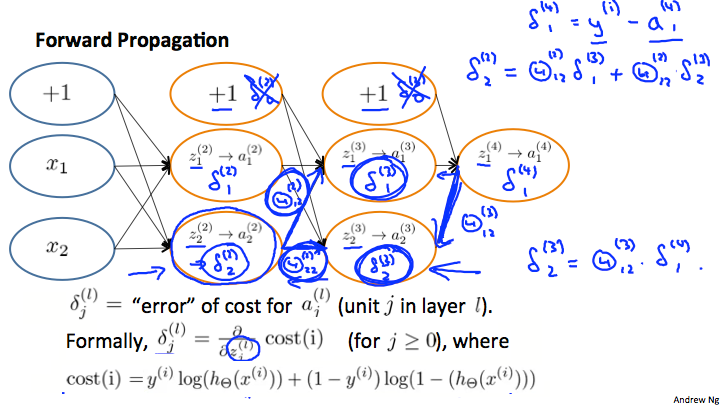
可以观察到 BP 算法两个突出特点：

自输出层向输入层（即反向传播），逐层求偏导，在这个过程中逐渐得到各个层的参数梯度。
在反向传播过程中，使用 δ(l)δ(l) 保存了部分结果，避免了大量的重复运算，因而该算法性能优异。

Implementation Nodte: Unrolling parameters

这一小节介绍如何使用Advanced optimization来计算神经网络，对于优化函数，前面有讲过，的定义如下:

function [jVal, gradient] = costFunction(theta)

...

optTheta = fminunc(@costFunction, initialTheta, options)

fminunc的第二个参数initialTheta需要传入一个vector，而我们之前推导的神经网络权重矩阵Θ显然不是一维的向量，对于一个四层的神经网络来说：

Θ矩阵： $Θ^{(1)}$ ， $Θ^{(2)}$ ， $Θ^{(3)}$ - matrices(Theta1, Theta2, Theta3)
梯度矩阵： $D^{(1)}$ ， $D^{(2)}$ ， $D^{(3)}$ - matrices(D1, D2, D3)

因此我们需要将矩阵转换为向量，在Octave中，可用如下命令

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]

这种写法会将3个Θ矩阵排成一维向量，假设 $Θ^{(1)}$ 是10x11的， $Θ^{(2)}$ 是10x11的， $Θ^{(3)}$ 是1x11的，也可以从thetaVector取出原始矩阵

Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)

总结一下：

前面得到的thetaVector代入到fminunc中，替换initialTheta
在costFunction中，输入的参数是thetaVec
```
  function[jVal,gradientVec] = costFunction(thetaVec)
```
在costFunction中，我们需要使用reshape命令从theVec取出 $Θ^{(1)}$ ， $Θ^{(2)}$ ， $Θ^{(3)}$ 用来计算FB和BP算法，得到 $D^{(1)}$ ， $D^{(2)}$ ， $D^{(3)}$ 梯度矩阵和 $J (Θ)$ ，然后再unroll $D^{(1)}$ ， $D^{(2)}$ ， $D^{(3)}$ 得到gradientVec

Gradient Checking

在计算神经网络的梯度时，要确保梯度计算正确，最好在计算过程中进行Gradient Checking。对于代价函数在某个点导数可近似为:

\frac{\partial}{\partial Θ} J (Θ) \approx \frac{J (Θ + ϵ) - J (Θ - ϵ)}{2 ϵ}

上面式子是单个Θ矩阵的梯度近似，对于过个Θ矩阵的梯度近似，计算方法相同:

\frac{\partial}{\partial Θ_{j}} J (Θ) \approx \frac{J (Θ_{1}, \dots, Θ_{j} + ϵ, \dots, Θ_{n}) - J (Θ_{1}, \dots, Θ_{j} - ϵ, \dots, Θ_{n})}{2 ϵ}

为了保证计算结果相近，其中 $ϵ = 10^{(-4)}$ ，注意过小的ϵ会导致计算问题，由于我们只能对一个Θ矩阵进行ϵ的加减，对于多个Θ矩阵，在Octave中需要使用循环计算

epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

得到近似的梯度之后，我们可以将计算得到的Appprox和上一节的deltaVector进行比较，查看是否gradApprox ≈ deltaVector，由于计算Approx代价很大，速度很慢，一般在确认了BP算法正确后，就不在计算Appox了

结合前一节做一个简单的总结:

通过实现BP算法得到δ矩阵DVec（Unrolled $D^{(1)}$ ， $D^{(2)}$ ， $D^{(3)}$ ）
进行梯度检查，计算gradApprox
确保计算结果足够相近
停止梯度检查，使用BP得到的结果
确保在用神经网络训练数据的时候梯度检查是关闭的，否则会非常耗时

###Random Initialization

计算神经网络，将theta初始值设为0不合适，这会导致在计算BP算法的过程中所有节点计算出的值相同。我们可以使用随机的方式产生Θ矩阵，比如将 $Θ_{ij}^{(l)}$ 初始化范围控制在[-ϵ,ϵ]：

Theta1=rand(10,11)*(2*INIT_EPSILON)-INIT_EPSILON #初始化10x11的矩阵
Theta1=rand(1,11)*(2*INIT_EPSILON)-INIT_EPSILON #初始化1x11的矩阵

rand(x,y)函数会为矩阵初始化一个0到1之间的实数，上面的INIT_EPSILON和上一节提到的ϵ不是一个ϵ。

小结

这一章先介绍了如何构建一个神经网络，包含如下几个步骤

第一层输入单元的个数 = 样本 $x^{(i)}$ 的维度
最后一层输出单元的个数 = 预测结果分类的个数
Hidden Layer的个数= 默认为1个，如果有多余1个的hidden layer，通常每层的unit个数相同，理论上层数越多越好

接下来介绍了如何训练一个神经网络，包含如下几步

随机初始化Θ矩阵
实现FP算法，对任意 $x^{(i)}$ 得出预测函数 $h_{Θ} (x^{(i)})$
实现代价函数
使用BP算法对代价函数求偏导，得到 $\frac{\partial}{\partial Θ_{i, j}^{(l)}} J (Θ)$ 的算式
使用梯度检查，确保BP算出的Θ矩阵结果正确，然后停止梯度检查
使用梯度下降或者其它高级优化算法求解权重矩阵Θ，使代价函数的值最小

不论是求解FP还是BP算法，都要loop每一个训练样本

for i = 1:m,
   Perform forward propagation and backpropagation using example (x(i),y(i))
   (Get activations a(l) and delta terms d(l) for l = 2,...,L

BP梯度下降的过程如下图所示：

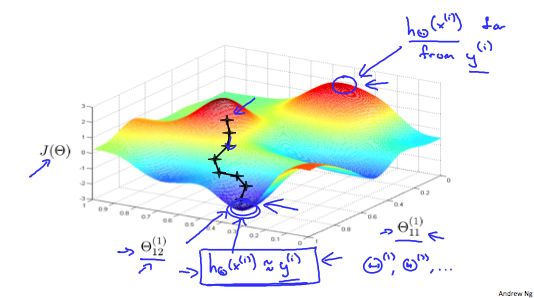
再回忆一下梯度下降，函数在极值点处的导数