调试

调试预测函数

假设我们设计了一个线性回归公式来预测房价，但是当我们用这个公式预测房价的时候结果却有很大的偏差，这时候我们该怎么做，可以尝试：

• 增加训练样本
• 减少样本特征集合
• 增加 feature
• 在已有 feature 基础上，增加多项式作为新的 feature 项($x_1^2,x_2^2,x_1{x}_2,$etc.)
• 尝试减小$\lambda$
• 尝试增大$\lambda$

具体该怎么做呢？显然满目的随机选取一种方法去优化是不合理的，一种合理的办法是实现 diagnostic 机制帮助我们找到出错点或者排除一些无效的优化方法

评估预测函数

当我们拿到训练样本时，可以把它分为两部分，一部分是训练集(70%)，一部分是测试集(30%)

• 训练集用$(x^{\mathrm{(1)}},y^{\mathrm{(1)}}),(x^{\mathrm{(2)}},y^{\mathrm{(2)}})...(x^{\mathrm{(m)}},y^{\mathrm{(m)}})$表示
• 测试集用$(x_{\mathrm{test}}^{\mathrm{(1)}},y_{\mathrm{test}}^{\mathrm{(1)}}),(x_{\mathrm{test}}^{\mathrm{(2)}},y_{\mathrm{test}}^{\mathrm{(2)}})...(x_{\mathrm{test}}^{\mathrm{(mtest)}},y_{\mathrm{test}}^{\mathrm{(mtest)}})$表示

使用这部分数据集的方法是：

1. 使用训练集，求$J_{train}(\Theta )$的最小值，得到$\Theta$

2. 使用测试集，计算$J_{\mathrm{test}}(\Theta )$

• 对于线性回归函数，计算$J_{\mathrm{test}}(\Theta )$的公式为：

$$J_{test}(\mathrm{\Theta <!--\; \Theta \; -->})={\displaystyle \frac{1}{2m_{test}}}\underset{i=1}{\overset{m_{test}}{\sum <!--\; \sum \; -->}}(h_{\mathrm{\Theta <!--\; \Theta \; -->}}(x_{test}^{(i)})-<!--\; -\; -->y_{test}^{(i)}{)}^2$$

• 对于逻辑回归函数，计算$J_{\mathrm{test}}(\Theta )$

$$J_{\mathrm{test}}(\Theta )=-\frac{1}{m_{\mathrm{test}}}{\displaystyle \sum _{i=1}^m[y_{\mathrm{test}}^{\mathrm{(i)}}\log <!--\; \; -->(h_{\mathrm{\theta <!--\; \theta \; -->}}(x_{\mathrm{test}}^{(i)}))+(1-<!--\; -\; -->y_{\mathrm{test}}^{(i)})\log <!--\; \; -->(1-<!--\; -\; -->h_{\mathrm{\theta <!--\; \theta \; -->}}(x_{\mathrm{test}}^{(i)}))]}$$

• 对于分类/多重分类问题，先给出错误分类的预测结果为

  $$err(h_{\mathrm{\Theta <!--\; \Theta \; -->}}(x),y)=\begin{array}{cc}1& \text{if }{h}_{\mathrm{\Theta <!--\; \Theta \; -->}}(x)\ge <!--\; \ge \; -->0.5andy=0or{h}_{\mathrm{\Theta <!--\; \Theta \; -->}}(x)<0.5andy=1\\ 0& \text{o}therwise\end{array}$$

  计算$J_{\mathrm{test}}(\Theta )$的公式为：

  $$\text{Test Error}={\displaystyle \frac{1}{m_{test}}}\underset{i=1}{\overset{m_{test}}{\sum <!--\; \sum \; -->}}err(h_{\mathrm{\Theta <!--\; \Theta \; -->}}(x_{test}^{(i)}),y_{test}^{(i)})$$

模型选择和训练样本重新划分

假设预测能后很好的 fit 我们的训练样本，也不能代表这个预测函数就是最好的，对于训练集以外的数据，预测函数的预测错误率可能高于训练样本的平均错误率。

在模型选择上，我们可能会纠结于如下几种模型：

1. $h_{\mathrm{(\theta )}}\left(x\right)={\theta }_{\mathrm{0</mi>}}+{\theta }_{\mathrm{1</mi>}}x$

   （d=1）

2. $h_{\mathrm{(\theta )}}\left(x\right)={\theta }_{\mathrm{0</mi>}}+{\theta }_{\mathrm{1</mi>}}x+{\theta }_{\mathrm{2</mi>}}{x}^2$
3. $h_{\mathrm{(\theta )}}\left(x\right)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_{\mathrm{}}{x}^3$
4. …
5. $h_{\mathrm{(\theta )}}\left(x\right)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+...+{\theta }_{10}{x}^{10}$

因此我们在选模型的时候需要考虑多项式的维度，即$d$为多少，此外我们还需要对原始的训练样本做进一步划分：

• 训练样本$(x^{\mathrm{(1)}},y^{\mathrm{(1)}}),(x^{\mathrm{(2)}},y^{\mathrm{(2)}})...(x^{\mathrm{(m)}},y^{\mathrm{(m)}})$ 占 60%
• 交叉验证样本$(x_{\mathrm{cv}}^{\mathrm{(1)}},y_{\mathrm{cv}}^{\mathrm{(1)}}),(x_{\mathrm{cv}}^{\mathrm{(2)}},y_{\mathrm{cv}}^{\mathrm{(2)}})...(x_{\mathrm{cv}}^{\mathrm{(mvc)}},y_{\mathrm{cv}}^{\mathrm{(mcv)}})$占比 20%
• 测试集$(x_{\mathrm{test}}^{\mathrm{(1)}},y_{\mathrm{test}}^{\mathrm{(1)}}),(x_{\mathrm{test}}^{\mathrm{(2)}},y_{\mathrm{test}}^{\mathrm{(2)}})...(x_{\mathrm{test}}^{\mathrm{(mtest)}},y_{\mathrm{test}}^{\mathrm{(mtest)}})$占 20%

然后我们可以按照下面步骤来对上面几种 model 进行评估：

1. 使用训练集，计算各自的$\Theta$值，用${\Theta }^{\mathrm{(d)}}$表示
2. 使用验证集，计算各自的$J_{\mathrm{cv}}(\Theta )$值，用$J_{\mathrm{cv}}({\Theta }^{\mathrm{(d)}})$，找到最小值
3. 将上一步得到最小值的 Θ 用测试集验证，得到通用的错误估计值$J_{\mathrm{test}}({\mathrm{\Theta }}^{(d)})$

观察 Bias 和 Variance

这一小节讨论模型多项式的维度 d 和 Bias 以及 Variance 的关系，用来观察模型是否有 overfitting 的问题。回一下 bias 和 variance 的概念, High bias 会造成模型的 Underfit，原因往往是多项式维度 d 过低，High variance 会造成模型的 Overfit，原因可能是多项式维度 d 过高。我们需要在两者间找到一个合适的 d 值。

• Training error,也就是$J\mathrm{(\theta )}$,由前面可知，公式为

$$J_{\mathrm{train}}(\theta )=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x_i)-y_i\right)}^2$$

• Cross Validation error 的公式为

$$J_{\mathrm{cv}}(\theta )={\displaystyle \frac{1}{2m_{\mathrm{cv}}}}\underset{i=1}{\overset{m_{\mathrm{cv}}}{\sum <!--\; \sum \; -->}}(h_{\mathrm{\theta }}(x_{\mathrm{cv}}^{(i)})-y_{\mathrm{cv}}^{(i)}{)}^2$$

二者的区别在于输入的数据集不同，以及$J_{\mathrm{cv}}(\theta )$输入样本少。我们建立一个坐标系，横轴是多项式维度 d 的值，从 0 到无穷大，纵轴是预测函数的错误率 cost of J(θ)，二者的关系是：

• 对于$J_{\mathrm{train}}(\mathrm{\theta })$（Training Error），当多项式维度 d 增大的时候，错误率逐渐降低
• 对于$J_{\mathrm{cv}}(\theta )$（Cross Validation Error），当多项式维度 d 增大到某个值的时候$J_{\mathrm{cv}}(\theta )$的值将逐渐偏离并大于$J_{\mathrm{train}}(\mathrm{\theta })$

如下图所示：

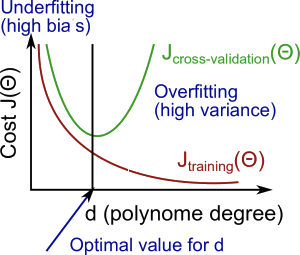
总结一下：

• High bias(Underfitting)：$J_{\mathrm{cv}}(\theta )$的值和$J_{\mathrm{train}}(\mathrm{\theta })$的值都很大，有$J_{\mathrm{cv}}(\mathrm{\theta })\approx J_{\mathrm{train}}(\mathrm{\theta })$
• High variance(Overfitting)：$J_{\mathrm{cv}}(\theta )$的值会小于$J_{\mathrm{train}}(\mathrm{\theta })$，在超过某个 d 值后会大于$J_{\mathrm{train}}(\mathrm{\theta })$的值

Regularization 项

参考之前对 Regularization 的介绍，λ 的值对预测函数的影响如下图所示

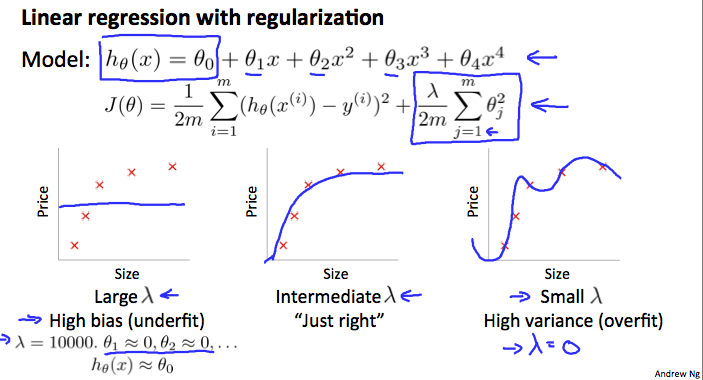
为了找到最适合的 λ 值，可以按如下步骤

1. 先列出一个 λ 数组： (i.e. λ∈{ 0, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24 })
2. 创建一系列不同 degree 的预测函数
3. 遍历 λ 数组，对每一个 λ 带入所有 model，求出$\Theta$
4. 将上一步得到的$\Theta$，使用交叉验正数据集计算$J_{\mathrm{cv}}(\Theta )$，注意$J_{\mathrm{cv}}(\Theta )$是不带 regularization 项的，或者 λ=0
5. 选出上面步骤中使$J_{\mathrm{cv}}(\Theta )$得到最小值的$\Theta$和 λ
6. 将上一步选出的$\Theta$和 λ 使用 test 数据集进行验证，看预测结果是否符合预期

绘制学习曲线

学习曲线是指横坐标为训练样本个数，纵坐标为错误率的曲线。错误率会随着训练样本变大，当样本数量超过某个值后，错误率增长会变慢，类似 log 曲线

• High bias - 样本数少：$J_{\mathrm{train}}(\Theta )$ 值很低，$J_{\mathrm{cv}}(\Theta )$值很高 - 样本数大：$J_{\mathrm{train}}(\Theta )$ 和 $J_{\mathrm{cv}}(\Theta )$都很高，当样本数超过某个值时，有$J_{\mathrm{train}}(\Theta )$ ≈ $J_{\mathrm{cv}}(\Theta )$ - 如果某个学习算法有较高的 bias，仅通过增加训练样本是没用的 - 学习曲线图如下所示

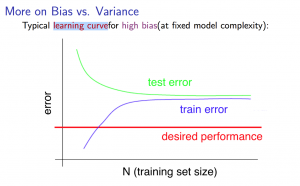
• high variance - 样本数少：$J_{\mathrm{train}}(\Theta )$ 值很低，$J_{\mathrm{cv}}(\Theta )$值很高 - 样本数大：$J_{\mathrm{train}}(\Theta )$ 升高，但还是保持在一个较低的水平。 $J_{\mathrm{cv}}(\Theta )$则持续降低，但还是保持在一个较高的水平，因此有$J_{\mathrm{train}}(\Theta )$ < $J_{\mathrm{cv}}(\Theta )$。两者的差值很大 - 如果某个学习算法有较高的 variance，通过增加训练样本有可能有帮助 - 学习曲线图如下所示

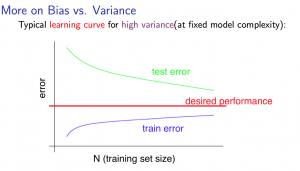
调试预测函数(Revisit)

呼应这一章第一节的内容，调试预测函数有如下几种办法：

• 增加训练样本数量 - 解决 high variance 问题
• 减少样本特征数量 - 解决 high variance 问题
• 增加样本特征 - 解决 high bias 问题
• 增加多项式维度 - 解决 high bias 问题
• 减小 λ 值 - 解决 high bias 问题
• 增大 λ 值 - 解决 high variance 问题

调试神经网络

• 一个层数少，每层 unit 个数少的神经网络，容易 underfitting，计算成本很低
• 一个层数多，每层 unit 个数也很多的神经网络，容易 overfitting，计算成本也很高，这种情况可加入 regularization 项（增大 λ）来尝试解决

对于神经网络，可以默认使用一层来求出 Θ，然后构建几个多层神经网络使用交叉数据样本进行验证，找到最合适的神经网络结构

Machine Learning System Design

这一章比较独立，以垃圾邮件分类器为例讲 Machine Learning 的系统设计。

对于垃圾邮件，通常来说会包含一些关键字，比如”discount”，”deal”等。我们用一个 nx1 的向量表示每一封邮件，向量中的每一项代表某个关键词是否出现，即如果这封 email 出现了某个关键词，那么对应向量中的该项的值为 1，否则为 0。向量长度为 1000<n<5000，如下图所示：

为了训练出准确的分类器模型，有哪些挑战

• 如何收集足够多的高质量训练数据，广告邮件，垃圾邮件等，这些训练数据的来源该去哪里获得
• 选取哪些作为关键的特征，比如邮件中出现”discount”,”deal”等，但是这些可能会误杀一些邮件，出了这些是否还是其它的信息可作为 feature
• 如何设计出全面严谨的模型，比如有些垃圾邮件会故意把某些单词拼错(e.g. m0rtage, med1cine, w4tches 等)来绕过反垃圾检查，训练模型要能识别出这些错误的拼写

当要实现一个 Machine Learning 系统时，推荐按照下列做法一步步做

1. 先从一个简单的算法开始，快速实现，在验证样本集中进行验证
2. 绘制学习曲线，观察是否需要增加训练样本或者增加特征
3. 进行误差分析，例如，在验证集中找出那些分类不准的 email，查看出错原因，观察能否找到一些共性或者系统性的错误

错误分析的的一个很重要的点是要使用的优化方法进行量化，比如使用 stemming 和未使用 stemming 的错误率对比

• Error Metrics for Skewed CLasses

所谓 Skewed Class 指的是分类问题中，对于某些结果出现的可能性很小，比如在患癌症的诊断中，癌症的样本占比很少，非癌症的训练样本很多，因此训练出来的模型，在预测结果上可能 99.5%都趋向于一个结果，这时我们怎么去衡量模型预测的准确率，需要引入”准确率”与”召回率”的概念：

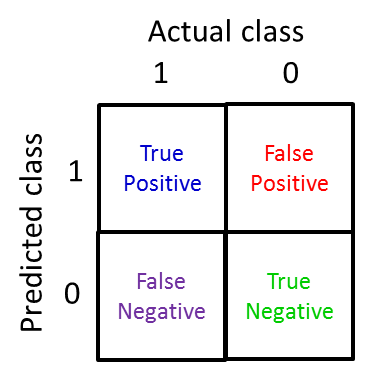
• 准确率(Precision)：precision = #(true positives)/#(predicted positives)
• 召回率(Recall): recall = #(true positives)/#(actual positives)

有时候准确率和召回率两者是矛盾的，较高的准确率可能会带来较低的召回率，反之亦然。

回忆之前逻辑回归的 sigmoid 公式，如果想要 y=1，需要$h_{\theta }\mathrm{(x)}>=0.5$，如果要追求较高的预测准确率，则需要调高阈值，比如我们希望在预测足够准确的情况下再通知病人他是否患有癌症，这时阈值就要设的较高，比如$h_{\theta }\mathrm{(x)}>=0.9$，但这会带来较低的召回率。同理，如果我们追求较高的召回率，则需要降低阈值，还是癌症的例子，我们希望尽量遗漏癌症的 case，哪怕有 30%的可能性也要提早通知病人治疗，这时阈值就要设的低一些，比如$h_{\theta }\mathrm{(x)}>=0.3$，但这又会带来较低的预测准确率

$$h_{\theta }\mathrm{(x)}>=\mathrm{threshold}$$

有什么办法可以帮助我们判断 threshold 的值到底好不好呢，可以使用 F 分数

$$F_1\mathrm{Score}:2\frac{PR}{P+R}$$

F 分数越大说明 threshold 计算出的值越合理，通常我们使用交叉验证样本集算出一个较好的 threshold 再使用测试集验证结果