Support Vector Machine
支持向量机 SVM(support vector machine)是另一种监督学习的算法,它主要用解决分类问题(二分类)和回归分析中。SVM 和前面几种机器学习算法相比,在处理复杂的非线性方程(不规则分类问题)时效果很好。在介绍 SVM 之前,先回顾一下 logistic regression,在逻辑回归中,我们的预测函数为:
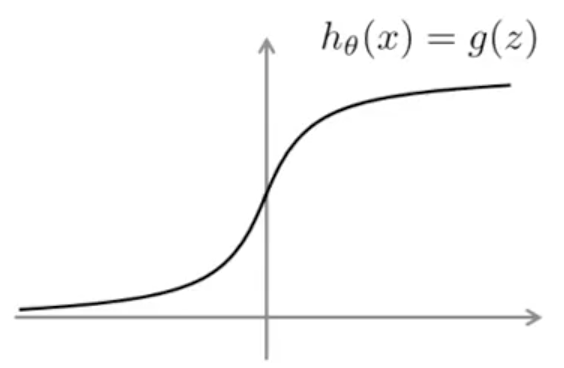
\[h_{\theta}(x) = g(\theta^T x) \quad g(z) = \frac{1}{1 + e^{-z}}\]- 如果要 $y = 1$,需要 $h_{\theta}(x) \approx 1$,即 $\theta^T x \gg 0$。
- 如果要 $y = 0$,需要 $h_{\theta}(x) \approx 0$,即 $\theta^T x \ll 0$。
预测函数在某点的代价函数为
\[\text{Cost of example}: -y \log(h_{\theta}(x)) - (1 - y) \log(1 - h_{\theta}(x))\]另 $z = \theta^T x$,带入上面式子得到
\[\text{Cost of example}: -y \log \left( \frac{1}{1 + e^{-\theta^T x}} \right) - (1 - y) \log \left( 1 - \frac{1}{1 + e^{-\theta^T x}} \right)\]- 当 $y = 1$ 时,后一项为零,上述式子为: $-\log \left( \frac{1}{1 + e^{-\theta^T x}} \right)$
- 当 $y = 0$ 时,后一项为零,上述式子为:$-\log \left( 1 - \frac{1}{1 + e^{-\theta^T x}} \right)$
对应的函数曲线为:
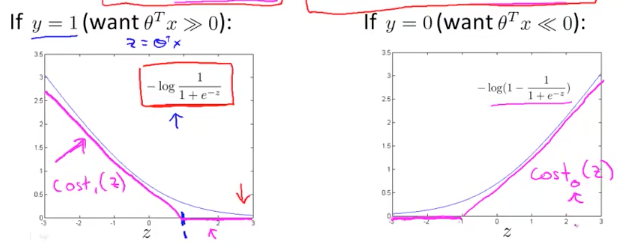
对于 SVM,我们使用粉色的函数来近似 cost function,分别表示为 $cost_1(z)$ 和 $cost_0(z)$,有了这两项,我们再回头看一下逻辑回归完整的代价函数:
\[\min_{\theta} \frac{1}{m} \left[ \sum_{i=1}^{m} \left( y^{(i)} (-\log(h_{\theta}(x^{(i)}))) + (1 - y^{(i)}) (-\log(1 - h_{\theta}(x^{(i)}))) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2\]用 $cost_1(z)$ 和 $cost_0(z)$ 替换中括号中的第一项和第二项,得到:
\[\min_{\theta} \frac{1}{m} \left[ \sum_{i=1}^{m} \left( y^{(i)} \cdot cost_1(\theta^T x^{(i)}) + (1 - y^{(i)}) \cdot cost_0(\theta^T x^{(i)}) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2\]去掉常量 m,将上述式子的表现形式上作如下变换
\[A + \lambda B \rightarrow CA + B\]对于逻辑回归,可以通过增大 $\lambda$ 值来提升 B 的权重,从而控制过度拟合。
在 SVM 中,可以通过减小 C 的值来提升 B 的权重,可以认为 $C = \frac{1}{\lambda}$,但是过大的 C 可能也会带来过度拟合的问题。
SVM 的 Cost 函数为:
\[\min_{\theta} C \left[ \sum_{i=1}^{m} \left( y^{(i)} \cdot cost_1(\theta^T x^{(i)}) + (1 - y^{(i)}) \cdot cost_0(\theta^T x^{(i)}) \right) \right] + \frac{1}{2} \sum_{j=1}^{n} \theta_j^2\]SVM 的预测函数为
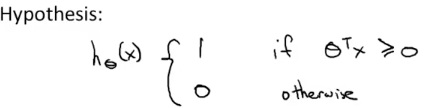
对于 和 ,它们的函数曲线如下图所示:

当 C 的值很大时,如果让 cost 函数的值最小,那么我们希望中括号里的值为 0,这样我们的优化目标就变成了:
-
如果要,我们希望,此时的值为 0
-
如果要,我们希望,此时的值为 0
先忽略数学求解,按照这个优化目标最后得出的 SVM 预测函数可以参考下图做直观的理解:
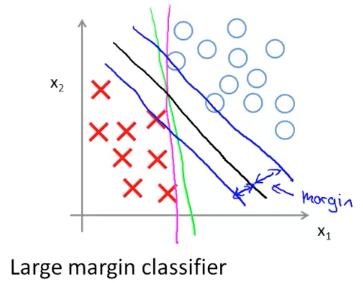
上图中,如果我们想要用一条曲线做为 Decision Boundary 来划分正负样本,可以有很多选择,比如绿线,粉线和黑线,其中黑线代表的预测函数为 SVM 分类模型,它的一个特点是样本到这条线的距离较其它预测函数比较大,因此 SVM 分类模型也叫做 Large Margin Classifier。
假设有向量 和 ,其中的长度为,我们想要求解向量 u 和 v 的內积:
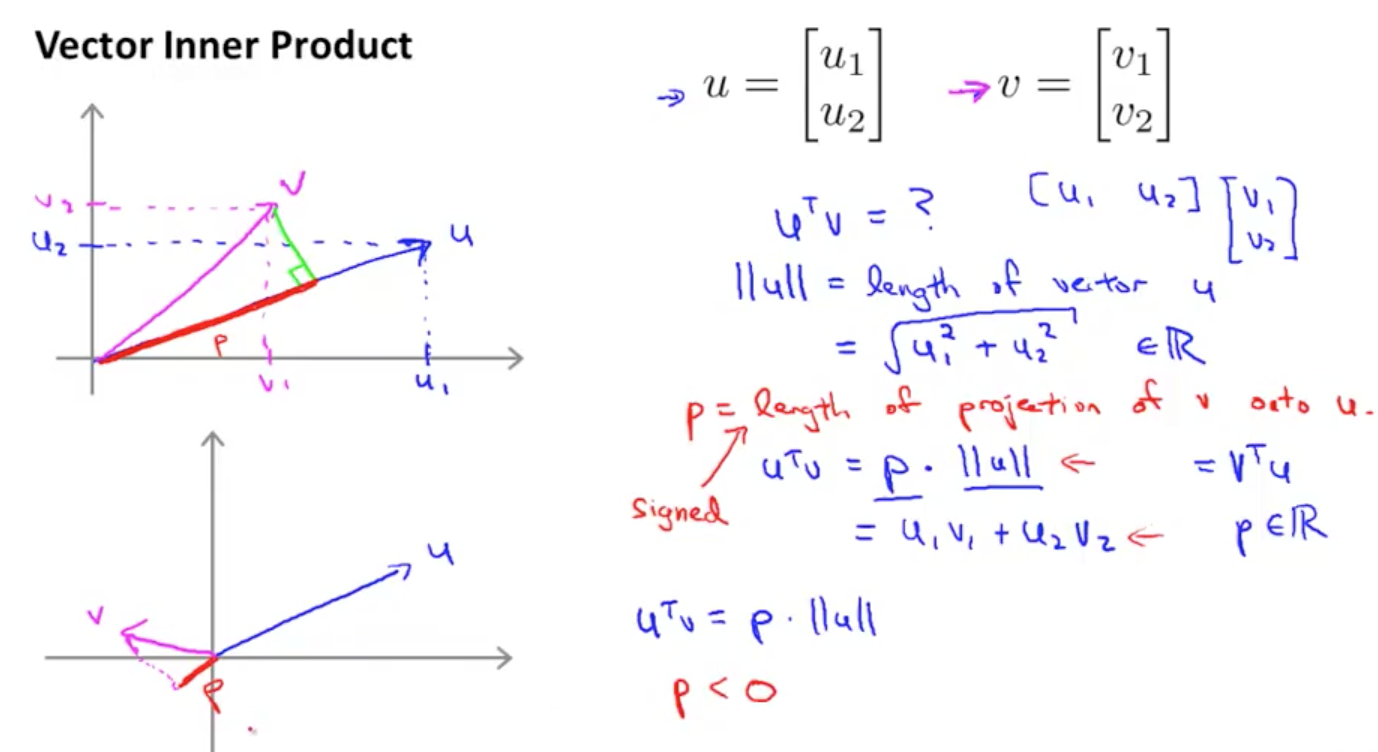
参考上图,定义 p 为向量 v 在 u 上的投影,有如下等式
其中 p 是有符号的,当 uv 夹角大于 90 度时,v 在 u 的投影 p 为负数。接下来我们用这个式子来求解 SVM 模型。
SVM 代价函数的优化目标为:
为了简化问题,我们令=0,令 n=2,上述优化方程简化为为:
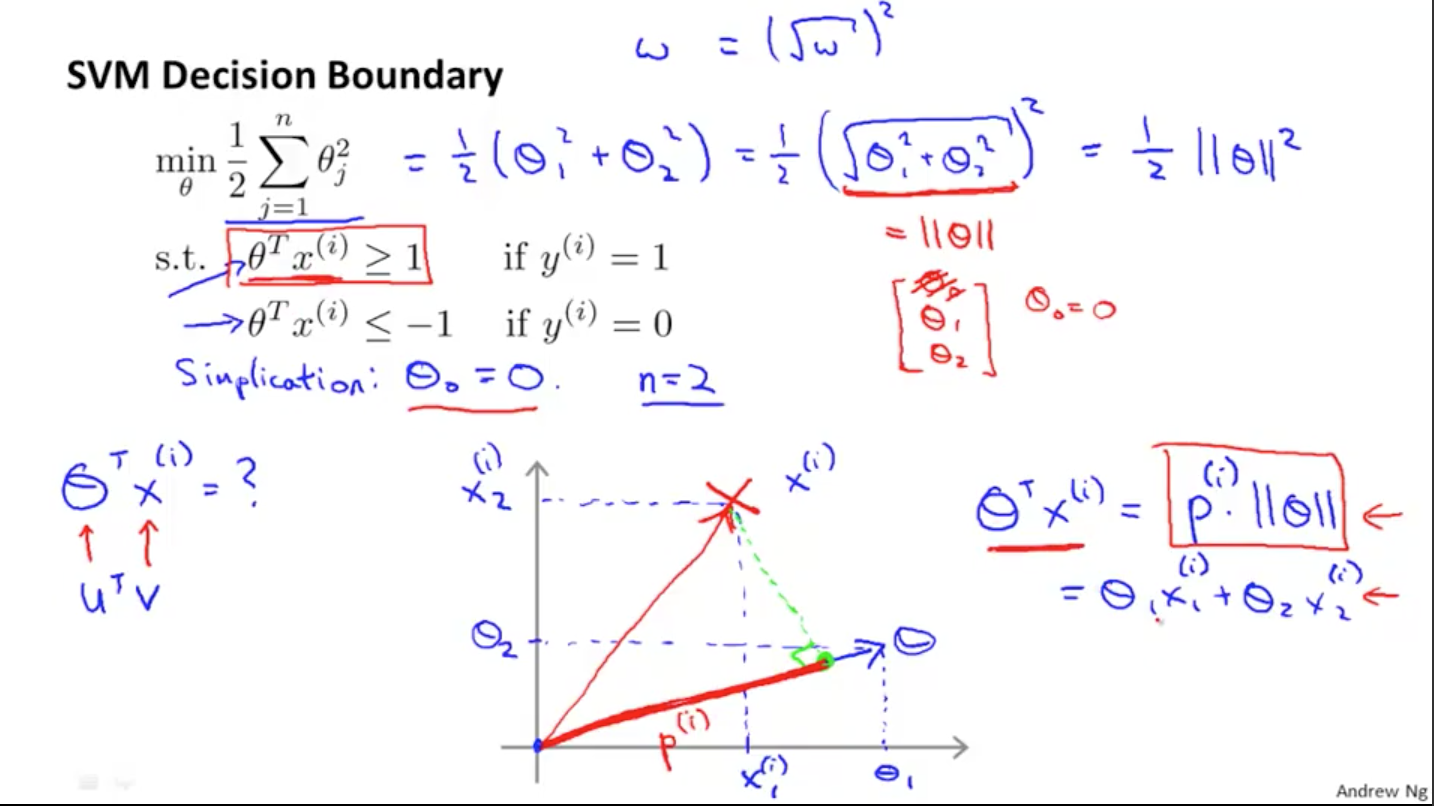
接下来考虑的替换,由前面可知,的内积可等价于向量 x 在向量 θ 上的投影 p 乘以 θ 的范数,如上图所示,即:
进而上面的优化目标变为:
接着我们用上面的视角再重新看待分类问题,如下图
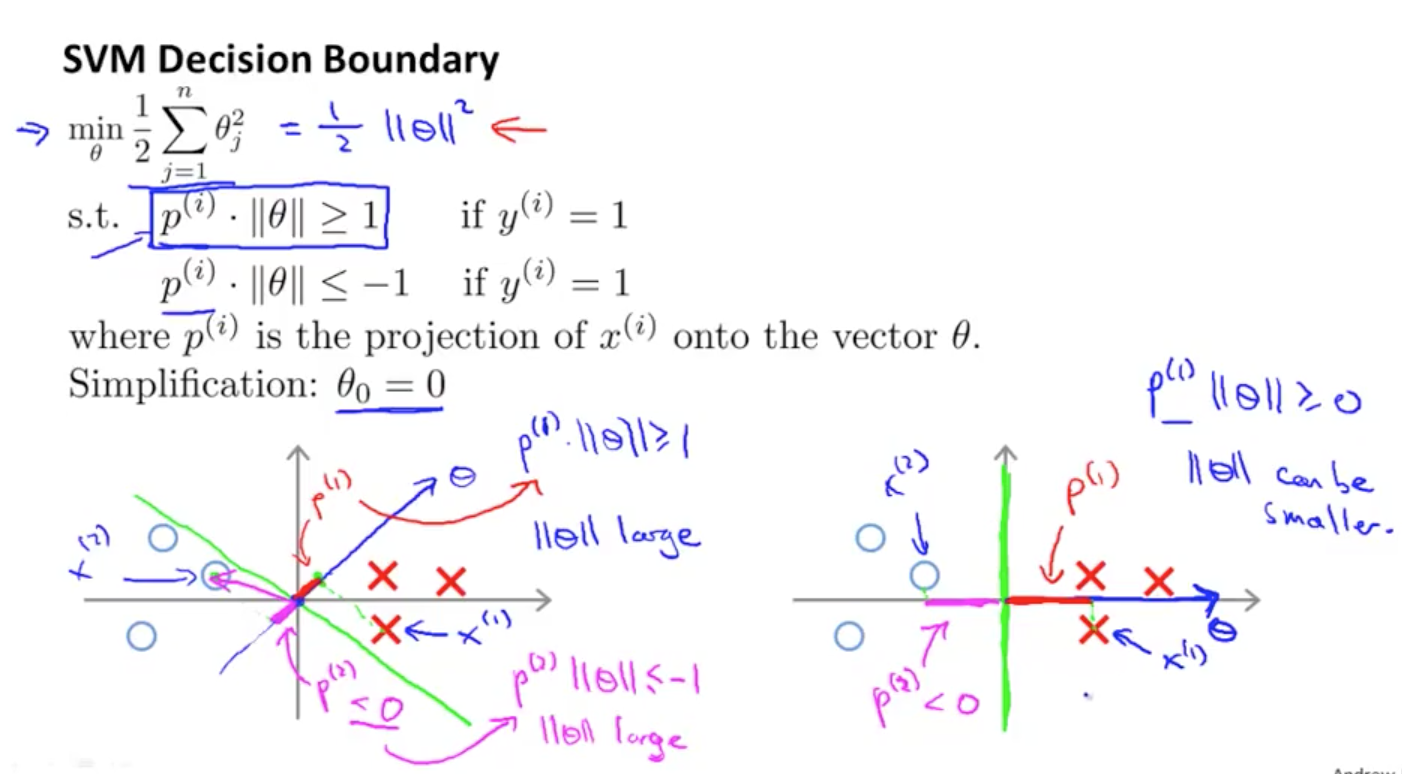
同样的样本数据,左图是用绿线做 Decision Boundary,正负样本 x 在 θ 上的投影 p 长度很小,对于的结果,要求那么则需要很大,而显然会使优化函数的值变大。因此这样的 Decision Boundary 是我们不想要的。右图的绿线是 SVM 模型的 Decision Boundary,按照上面的推理可以看出,SVM 模型得到的比左边的要小,进而使优化函数能得出更优解。注意的是,可以使 Decision Boundary 穿过原点,即使,结论也依旧成立。
上面解释了 SVM 也叫做 Large Margin Classifier 的原因。接下来讨论如何使用 SVM 解决复杂非线性分类方程,也叫做求解 Kernels 。
假设有一系列非线性样本如下图:
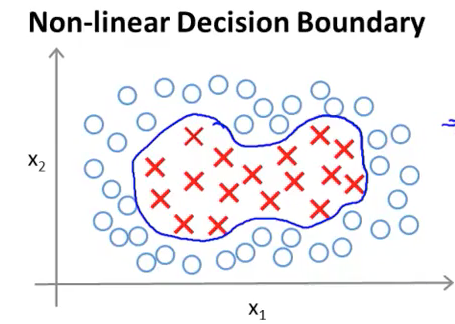
我们使用一个非线性方程来描述 Decision Boundary(上图蓝线):
用替换多项式中的,有
其中:
显然这种构造方式是由于样本特征数量有限,我们需要使用样本的一系列高阶组合来当做新的 feature 从而产生高阶多项式。但是对于特征的产生,即的取值有没有更好的选择呢?接下来我们使用 kernal 来产生新的 feature
给定任一个样本值,定义为:
其中:
-
成为 Landmark ,每个标记点会定义一个新的 feature 变量,选取方式在后面将会介绍
- similarity 函数称为 Kernel 函数,Kernel 函数有多种,在上述公式中,kernel 函数为高斯函数,有时也记作:
- 假设,则有
- 假设和 landmark,即很远,则有
-
给定一个新的样本,我们可以计算的值
- 高斯核函数 Octave 实现
function sim = gaussianKernel(x1, x2, sigma)
%RBFKERNEL returns a radial basis function kernel between x1 and x2
% sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
% and returns the value in sim
x1 = x1(:); x2 = x2(:);
sim = e^(-(sum((x1-x2).^2)/(2*sigma^2)));
% =============================================================
end
假如我们有一个 landmark:,,令,下图是 Kernel 函数的可视化呈现:
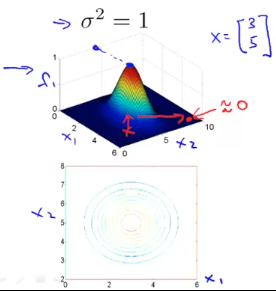
当给定的样本点 更靠近 时,更接近最大值 1。同理,离得更远则 更接近于 0。接下来我们观察对 f 曲线的影响
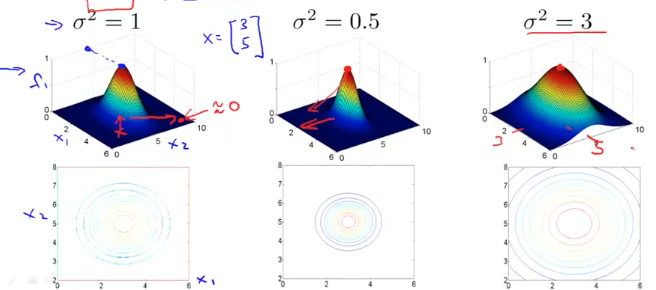
- 上图可以看到当越小时,f 下降到 0 的速度越快,反之则越慢
当我们计算出的值之后,给定 θ 值,我们就能绘制预测函数了,如下图:
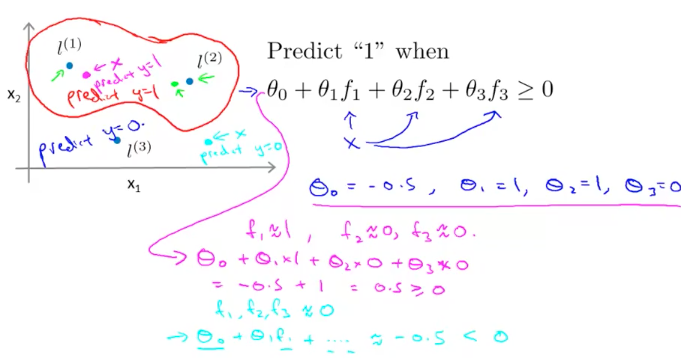
假设我们有一个样本(粉色的点),显然它更靠近,因此有:
因此这个样本点的分类结果为。同理,对于另一个样本点(绿色的点),它距离三个 landmark 都很远,因此有
因此这个样本点的分类结果为。接下来我们讨论如何选择则 Landmark。
通常来说在给定一组训练样本之后,我们把每个样本点标记为一个 landmark,如图所示
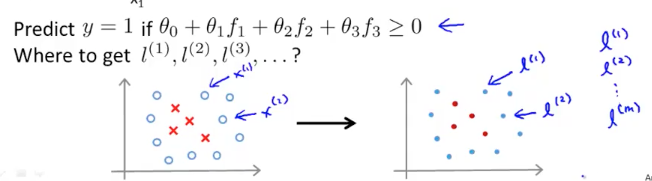
具体来说,给定训练样本: ,使 ,对于任意训练样本,计算向量:

在得到向量后,我们可以构建预测函数
带入 cost 函数,通过最优化解法,计算出 θ 值。注意下面给出的 cost 函数和上面给出的 cost 函数有一点不同,这里使用第的 kernal 函数的结果代替原先在的样本值。SVM 的最优化算法实际上是凸优化问题,好的 SVM 软件包可以求出最小值,不需要担心局部最优解的问题
最后还要说明几点:
-
某些 SVM 算法,在 Regularization 一项会有不同的表示方式,有的将 表示为 ,数学上是等价的。也有些算法为了计算效率将其表示为,为样本数量,暂不关心其中的细节。对于最优化函数的解法,这个课程不讨论,调用现有的函数即可。
-
SVM 参数 - 选择的值。值很大,会造成较低偏差(bias),但会带来较高的方差(variance),有 overfit 的趋势;值很小,会造成较高的偏差和较低的方差,有 underfit 的趋势。
- 选择<math><msup><mi>σ</mi><mn>2</mn></msup></math>的值,<math><msup><mi>σ</mi><mn>2</mn></msup></math>越大,<math><mi>f</mi></math>下降的越平滑,会导致样本点<math><msup><mi>x</mi><mi>(i)</mi></msup></math>据landmark点<math><msup><mi>l</mi><mi>(i)</mi></msup></math>的距离偏大,从而带来较大的偏差和较低的方差,有underfit的趋势。<math><msup><mi>σ</mi><mn>2</mn></msup></math>越小,<math><mi>f</mi></math>下降速度越快,越陡峭,会带来较低的偏差和较高的方差,有overfit的趋势。 -
参数选择的 Octave 实现思路
function [C, sigma] = dataset3Params(X, y, Xval, yval)
%DATASET3PARAMS returns your choice of C and sigma for Part 3 of the exercise
%where you select the optimal (C, sigma) learning parameters to use for SVM
%with RBF kernel
% [C, sigma] = DATASET3PARAMS(X, y, Xval, yval) returns your choice of C and
% sigma. You should complete this function to return the optimal C and
% sigma based on a cross-validation set.
%
% You need to return the following variables correctly.
C = 1;
sigma = 0.3;
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return the optimal C and sigma
% learning parameters found using the cross validation set.
% You can use svmPredict to predict the labels on the cross
% validation set. For example,
% predictions = svmPredict(model, Xval);
% will return the predictions on the cross validation set.
%
% Note: You can compute the prediction error using
% mean(double(predictions ~= yval))
%
values = [ 0.01, 0.03, 0,1, 0.3, 1, 3, 10, 30 ];
max_error = Inf;
for c = values;
for s = values;
model = svmTrain(X, y, c, @(x1, x2) gaussianKernel(x1, x2, s));
predictions = svmPredict(model, Xval);
error = mean(double(predictions ~= yval));
if error < max_error;
max_error = error;
C=c;
sigma=s;
end;
end
end;
% =========================================================================
end
SVM 编程实现思路
接下来讨论如何编程实现 SVM,前面提到,SVM 给出了一个优化目标和求解最优解问题,最优解的求解可以通过使用一些库来完成,比如liblinear,libsvm等。我们只需要
- 给出参数的值
- 给出 Kernel 的核函数 - 如果样本特征很大,而样本数量很少的的情况下使用,可以选择”No kernel”,所谓”No kernel”实际上就是”Linear kernel”,使用线性方程 来判定值 - 如果样本特征很少,而样本数量很大,可以选择高斯 kernel,使用高斯 kernel 要注意几点 - 给出合适的的值。 - 对样本进行 feature scaling,不同 feature 间的数量级可能不同,避免范数计算产生较大偏差,对 feature 要进行归一化 - 如果要使用其它的核函数,要确保该核函数满足”Mercer’s Theorem”,这样 SVM 库才能对核函数进行通用的最优化求解 - 对于多个核函数,选择在交叉验证数据集表现最好的核函数
对于多个分类结果的场景,许多 SVM 库提供了函数可直接调用。或者采用之前提到的 one-vs-all 的方式

Logistic regression vs. SVM
我们用表示样本特征数量,用表示样本数量
- 如果 (n=10,000,m=10~1000),比如 Spam 邮件过滤,有几千个关键词作为 feature,而邮件数量即样本数量要明显少于特征数量,这时可以使用逻辑回归或者 SVM 线性核函数
- 如果 很小(1 ~ 1000),处于中等数量级(10 ~ 10000),这时可以使用 SVM 高斯核函数
- 如果 很小(1 ~ 1000),很大(几十万),这种情况下使用 SVM 高斯核函数会很慢,这时需要增加更多的 feature,然后使用逻辑回归或者线性 SVM
- 对于神经网络来说没有这些限制,但是训练起来比较慢
