非监督学习

• 监督学习，它的特点是对已知样本产生的结果是有预期的，因此我们可以对样本进行标记，Training Set 可以表示为$\left\{\right(x^{\mathrm{(1)}},y^{\mathrm{(1)}}),(x^{\mathrm{(2)}},y^{\mathrm{(2)}}),...,(x^{\mathrm{(m)}},y^{\mathrm{(m)}}\left)\right\}$
• 非监督性学习对样本产生的结果是无法预期的，因此无法对样本数据进行标，Training Set 可表示为$\{x^{\mathrm{(1)}}{x}^{\mathrm{(2)}},...,x^{\mathrm{(m)}}\}$，非监督学习要做的是在这些无标注的数据中寻找某种规则或者模式。比如将数据归类，也叫做聚类( Clustering )就是一种非监督学习算法

K-Means 算法

K-Means 是解决分类问题的一种很常用的迭代算法，具体步骤如下(以 K=2 为例)

• 在数据集中随机初始化两个点（红蓝叉），作为聚类中心(Cluster Centrioid)

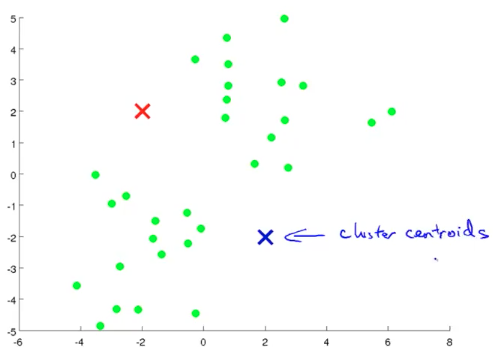
• 对样本进行簇分配（Cluster Assignment）：对数据集中的所有样本计算到聚类中心的距离，按照样本据某个中心点距离远近进行归类

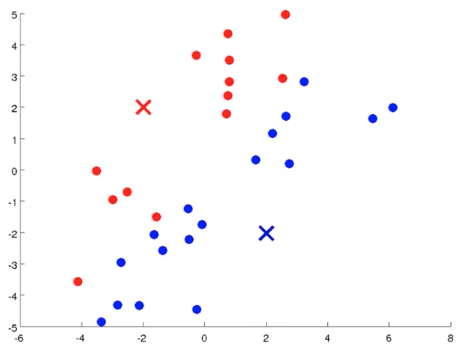
• 移动聚类中心 (Move Centroid): 对分类好的样本，求平均值，得到新的聚类中心

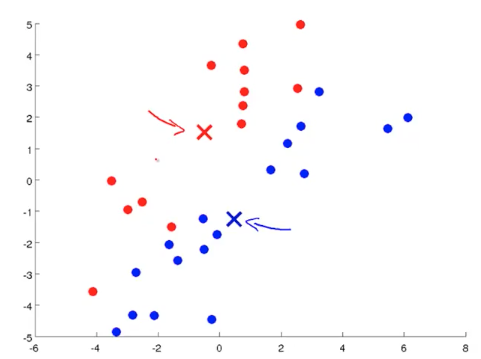
• 重复上述两个步骤，直到中心点不再变化

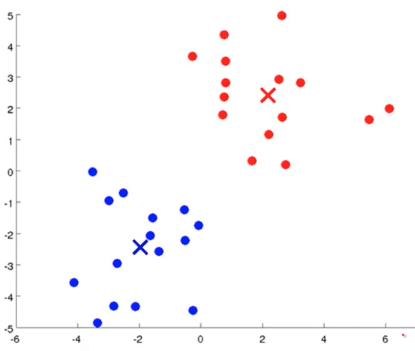
K-Means 函数的输入有两个参数：聚类数量 K 和训练集（默认$x_0=0$ )

随机初始化 K 个聚类中心点:${\mu }_1,{\mu }_1...,{\mu }_k$

Repeat{

//index of cluster(1,2,…K) to which example $x^{\mathrm{(i)}}$ is currently assigned
$\text{end}$

</br>

}

• 第一步的 Octave 实现为：

function idx = findClosestCentroids(X, centroids)

	% Set K
	K = size(centroids, 1);

	% You need to return the following variables correctly.
	idx = zeros(size(X,1), 1);


	for i=1:size(X,1)
	    d_min=Inf;
	    for k=1:K
	        d=sum((X(i,:)-centroids(k,:)).^2); %这一步也可以用向量化实现
	        %  
	        %	 diff = X(i, :)'-centroids(k, :)';
	    	 %	 d = diff'*diff;
	        %
	        if d<d_min
	            d_min=d;
	            idx(i)=k;
	        end  
	    end
	end
end

• 第二步的 Octave 实现为：

function centroids = computeCentroids(X, idx, K)

	% Useful variables
	[m n] = size(X);
	centroids = zeros(K, n);

	for k=1:K
	    num=0;
	    sum=zeros(1,n);
	    for i=1:m
	        if (k==idx(i))
	            sum=sum + X(i,:);
	            num=num+1;
	        end
	    end
	    centroids(k,:)= sum/num;
	end

end

• K-Means 的优化目标函数为：找到$c^{\mathrm{(1)}},...,c^{\mathrm{(m)}},...,{\mu }_1,...,{\mu }_k$使$J$最小：

• 其中 - $c^{\mathrm{(i)}}$:样本$x^{\mathrm{(i)}}$被分配到某个聚类的 index 值，例如：$x^{\mathrm{(i)}}->5$，则$c^{\mathrm{(i)}}=5$ - ${\mu }_k$:聚类中心点 - ${\mu }_{c^{\mathrm{(i)}}}$:样本$x^{\mathrm{(i)}}$被分配到某个聚类的中心点，例如：$x^{\mathrm{(i)}}->5$，$c^{\mathrm{(i)}}=5$，${\mu }_{c^{\mathrm{(i)}}}={\mu }_5$
  • J 也叫做Distortion Function，在实际求解上，参照上一节提供的步骤运算更好理解。

前面提到了在进行 K-Means 运算之前要先随机初始化 K 个聚类中心点:${\mu }_1,{\mu }_1...,{\mu }_k$（$K<m$）,通常的做法是在训练样本中随机选取$K$个样本作为${\mu }_1,{\mu }_1...,{\mu }_k$的值，即${\mathrm{\mu <!--\; \mu \; -->}}_1=x^{(i_1)},{\mathrm{\mu <!--\; \mu \; -->}}_2=x^{(i_2)},\dots <!--\; \dots \; -->,{\mathrm{\mu <!--\; \mu \; -->}}_k=x^{(i_k)}$。如果随机选取的样本点不理想，均值点很可能会落到 local optima，如下图所示：

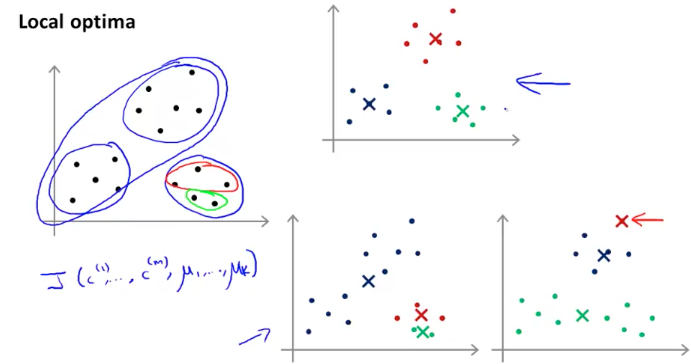
为了避免这种情况出现，我们可以尝试多次计算:

For i = 1 to 100 {

1. Randomly initialize K-means.

2. Run K-means. Get $c^{\mathrm{(1)}},...,c^{\mathrm{(m)}},...,{\mu }_1,...,{\mu }_k$

3. Compute cost function(distortion) $J(c^{\mathrm{(1)}},...,c^{\mathrm{(m)}},...,{\mu }_1,...,{\mu }_k)$

}

4 . Pick clustering that gave lowest cost $J(c^{\mathrm{(1)}},...,c^{\mathrm{(m)}},...,{\mu }_1,...,{\mu }_k)$

维数约减 Dimensionality Reduction

对于多维度的样本数据我们希望可以将其缩减到低维度，这样可以对数据进行可视化处理，便于观察和理解数据。例如将二维数据映射到一维，3 维数据映射到二维，映射过程主要是通过投影完成

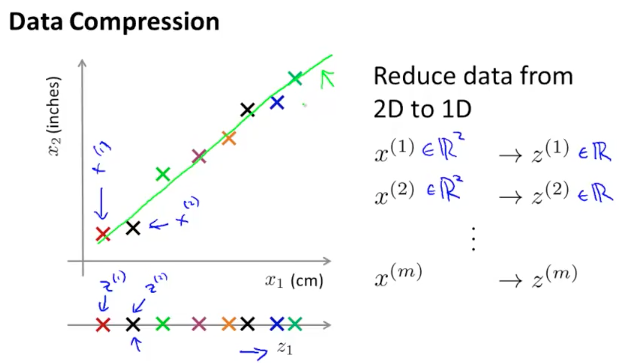
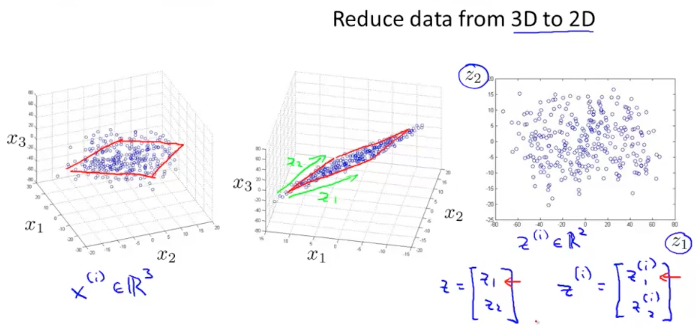
一种常用的降维算法叫做主成分分析PCA( Principal Compoent Analysis)，它可以将$n$维数据映射成$k$维数据。具体来说，是找到$k$个向量$u^{\mathrm{(1)}},u^{\mathrm{(2)}},...,u^{\mathrm{(k)}}$，使各个数据点在该向量上的投影误差（距离）最小。通俗的说，PCA 就是尝试寻找一个低维平面将高维度数据投影到这个平面，且各个点到该平面的垂直距离最短（误差最小）

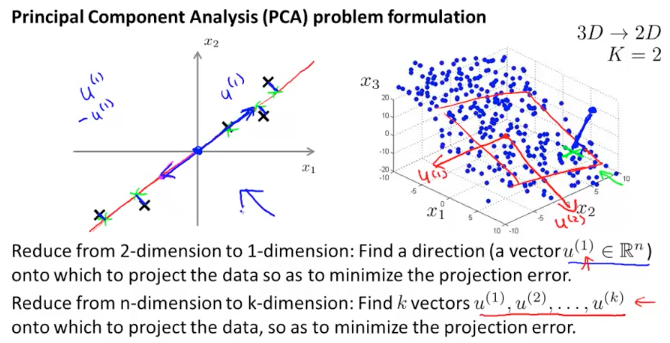
在使用 PCA 之前，通常要对数据进行预处理，使样本保持在统一数量级上。假设有训练样本：$\{x^{\mathrm{(1)}}{x}^{\mathrm{(2)}},...,x^{\mathrm{(m)}}\}$，对其进行 feature scaling(mean normalization):

接下来要解决两个问题，一是怎么计算投影平面$[u^{\mathrm{(1)}},u^{\mathrm{(2)}},...,u^{\mathrm{(k)}}]$，而是怎么计算平面中的点

• 我们定义投影平面为$U_{\text{reduce}}$，维度为：nxk
• 平面中的点构成的矩阵为$Z$维度为 kx1

第一步先计算协方差矩阵得到 sigma 矩阵$\sum$

向量化实现为:

其中$x^{\mathrm{(i)}}$为$n\_1$矩阵，因此$\sum$ 为 $n\_\mathrm{n}$。

第二步计算$\sum$的特征值和特征向量，Octave 可直接使用 svd 函数对矩阵进行奇异值分解:

[U,S,V] = svd(Sigma)

在返回的三个结果中，$U$为 nxn 矩阵，我们从中取出前$k$列，得到$U_{\text{reduce}}$矩阵，既是我们想要的投影平面

第三步计算$Z$矩阵：

其中，$U_{\text{reduce}}^T$为 kxn 的矩阵，x 为 nx1 的矩阵，因此$Z$为 kx1 的矩阵

总结一下上述过程的 Octave 实现为:

Sigma = (1/m) * X'*X;
[U,S,V] = svd(Sigma);

Z = zeros(size(X, 1), K);

U_reduce = U(:, 1:K);
for i=1:size(X,1)
    x = X(i, :)';
    Z(i,:) = x' * U_reduce;
end

这部分涉及到一些的数学推导，需要理解矩阵的特征值，特征向量，奇异值分解以及协方差矩阵的物理意义等等，此处暂时忽略这些概念，把 PCA 当做黑盒来看待

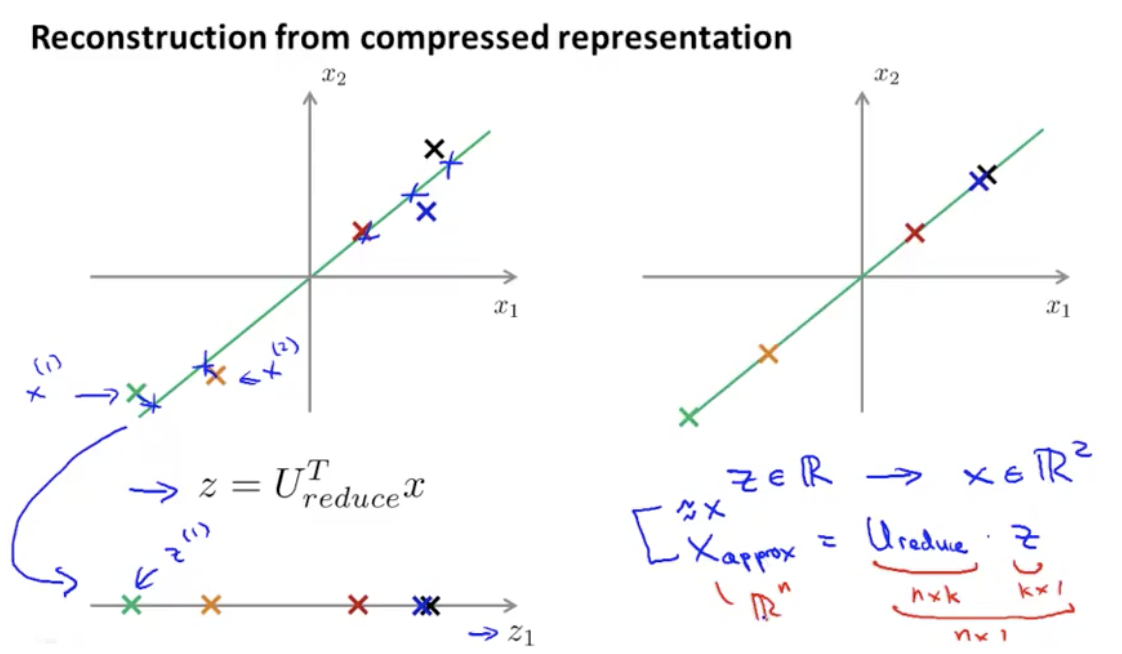
当我们有了低维度的$Z$，如何还原出高维度的$X$，可通过如下式子：

这里，$U_{\text{reduce}}^T$是 nxk 的，$Z$是 kx1 的，$X_{\text{approx}}$是 nx1 的, matlab 实现为:

function X_rec = recoverData(Z, U, K)

	X_rec = zeros(size(Z, 1), size(U, 1));
	for i=1:size(Z,1)
	    v=Z(i,:)';
	    X_rec(i,:)=v' * U(:, 1:K)';
	end
end

接下来的问题是如何选择$k$值，使用下面公式：

其中，分子为样本平均投影误差的平方和，分母为样本数据的平均方差和，选取最小的$k$值，使比值小于等于 0.01。这个式子的意思是“在保留了 99%的样本差异性的前提下，选择了 K 个主成分”，具体的做法如下：

• 选取$k=1$
• 计算$U_{\text{reduce}},z^{\mathrm{(1)}},z^{\mathrm{(1)}}...,z^{\mathrm{(m)}},x_{\text{approx}}^{\mathrm{(1)}},...,x_{\text{approx}}^{\mathrm{(m)}}$
• 检查上述式子结果是否满足条件，如果不满足，重复第一步令$k=k+1$

如果使用 Octave，在[U,S,V] = svd(Sigma); 的返回值中，S矩阵是一个对角阵，我们可以用这个矩阵简化对$k$值的计算：对于给定的任意$k$值，计算

通常情况下选取$k=1$，缓慢增大$k$值，观察上面式子计算结果。这种方式的好处是只需要计算一次svd得到$S$即可，比较高效