异常检测

Posted on 2017-11-08 | In Machine Learning , AI

异常检测主要是通过概率模型对输入的样本数据进行判定，判断是否为异常数据。比如在线购物网站识别用户的异常行为，飞机部件出厂检测，电脑状态检测等。以电脑监控为例，可以使用如下几个值很大或者很小的 feature：

$ x_1 = \thinspace memeory \thinspace use \thinspace of \thinspace the \thinspace computer $
$ x_2 = \thinspace number \thinspace of \thinspace disk \thinspace accesses \thinspace etc $
$ x_3 = \thinspace CPU \thinspace load $
$ x_4 = \thinspace network \thinspace traffic $
$ x_5 = \thinspace CPU \thinspace load \thinspace / \thinspace network \thinspace traffic $
$ x_6 = \thinspace CPU {load^2} \thinspace / \thinspace network \thinspace traffic $

我们的目标就是构建一个概率模型，对任意输入 $x$ 判断其是否是异常数据。在介绍具体算法之前，先回顾一下高斯分布：

p (x) = \frac{1}{\sqrt{2 π} σ} \exp (- \frac{(x - μ)^{2}}{2 σ^{2}})

其中：

期望： $μ = \frac{1}{m} \sum_{i = 1}^{m} x^{(i)}$ 表示样本的均值，极大似然估计值
方差： $σ^{2} = \frac{1}{m} \sum_{i = 1}^{m} (x^{(i)} - μ)^{2}$ 表示样本的与均值之间的平均偏差，方差越大，曲线越扁平；方差越小，曲线越陡峭
如果某种数据样本符合高斯分布，记作 $X ~ N (μ, σ^{2})$ ，高斯分布也叫做正态分布(Normal Distribution)

给定训练集 ${x^{(1)} x^{(2)}, ..., x^{(m)}}$ ， $x$ 属于 n 维并服从高斯分布: $x_{i} ~ N (μ_{i}, σ_{i}^{2})$ 异常检测的概率模型如下：

P (x) = P (x_{1}; μ_{1}, σ_{1}^{2}) P (x_{2}; μ_{2}, σ_{2}^{2}) ... P (x_{n}; μ_{n}, σ_{n}^{2}) = Π_{j = 1}^{n} P (x_{j}; μ_{j}, σ_{j}^{2})

检测步骤如下：

选取特征数据 $x_{j}$
计算每个特征的 $μ_{1} ... μ_{n}, σ_{1}^{2} ... σ_{n}^{2}$ $μ_{j} = \frac{1}{m} \sum_{i = 1}^{m} x_{j}^{(i)}$

σ_{j}^{2} = \frac{1}{m} \sum_{i = 1}^{m} (x_{j}^{(i)} - μ_{j})^{2}

Octave 代码如下:

function [mu sigma2] = estimateGaussian(X)

[m, n] = size(X);
mu = zeros(n, 1);
sigma2 = zeros(n, 1);

for i=1:n
    mu(i)  = (1/m)*sum(X(:,i));
    sigma2(i) =  (1/m)*sum((X(:,i)-mu(i)).^2);
end

end

对新的输入样本 $x$ ,计算 $p (x)$ ，根据阈值判断是否为异常数据 $P (x) < ε$

P (x) = Π_{j = 1}^{n} P (x_{j}; μ_{j}, σ_{j}^{2}) = Π_{j = 1}^{n} \frac{1}{\sqrt{2 π} σ_{j}} \exp (- \frac{(x - μ_{j})^{2}}{2 σ_{j}^{2}})

接下来的问题是，对于不服从高斯分布的样本，我们怎么将其转化为高斯分布样本

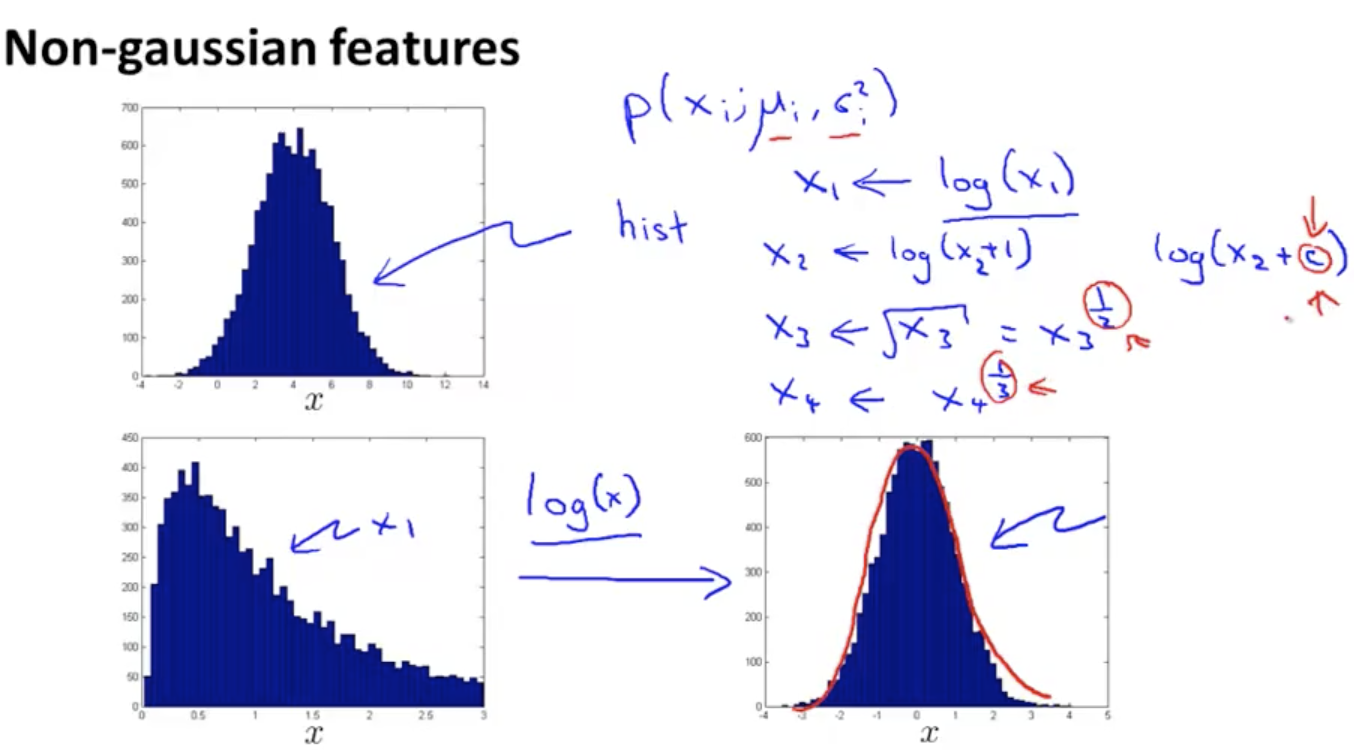
如上图所示，如果样本数据不服从高斯分布，可以使用 $log$ 或指数来调整样本分布。另外，上述模型对某些异常数据可能无法区分，我们希望：

对于正常的样本数据 $x$ ， $p (x)$ 值很大
对于异常的样本数据 $x$ ， $p (x)$ 值很小

但是对于某些异常数据， $P (x)$ 可能也很大，它们在各自样本分布曲线中均处于正常范畴，但是在二维高斯函数分布中却属于异常数据这时我们需要对异常数据进行分析，如下图所示

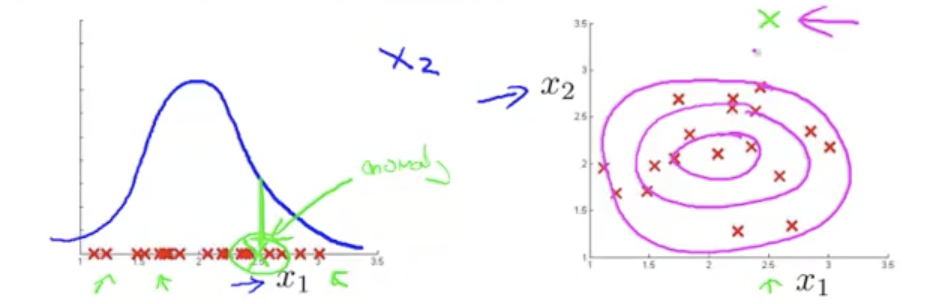
因此我们要优化之前的模型，相比原来独立计算各维度的概率，优化后的模型使用协方差来表示各维度之间的关系：

P (x; μ, \sum) = \frac{1}{(2 π)^{n/2} | \sum |^{1/2}} \exp (- \frac{1}{2} (x - μ)^{T} \sum^{-1} (x - μ))

其中 $μ$ 为 N 维矩阵， $μ = \frac{1}{m} \sum_{i = 1}^{m} x^{(i)}$
$\sum$
为 NxN 协方差矩阵， $\sum = \frac{1}{m} \sum_{i = 1}^{m} (x^{(i)} - μ) (x^{(i)} - μ)^{T}$

多元高斯函数以及协方差的变化对其影响如下：

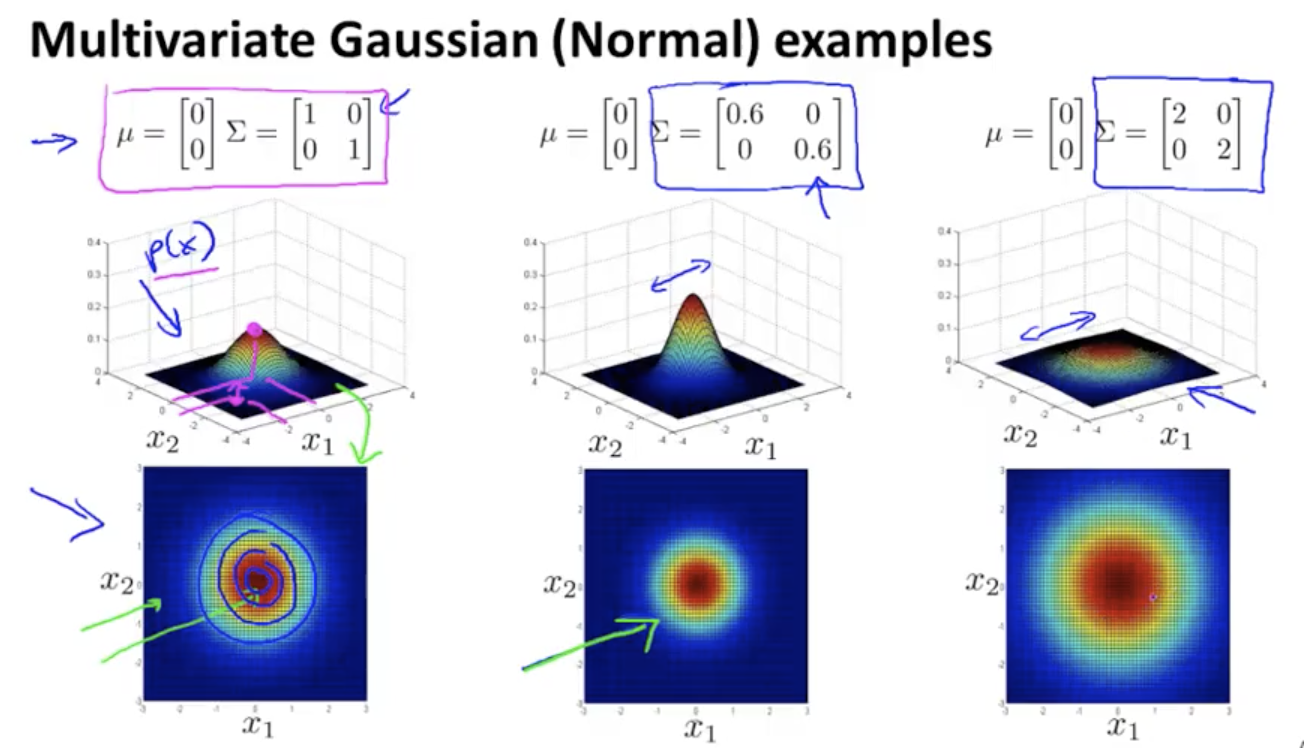
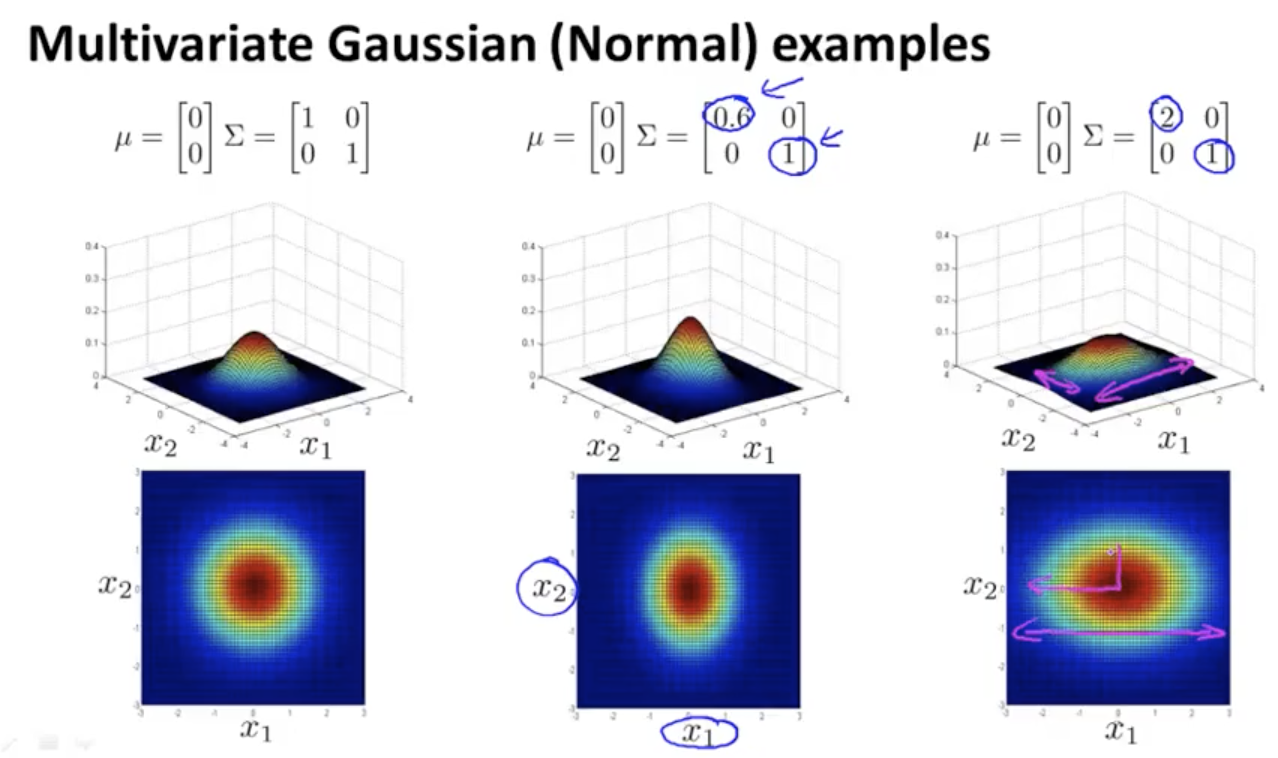
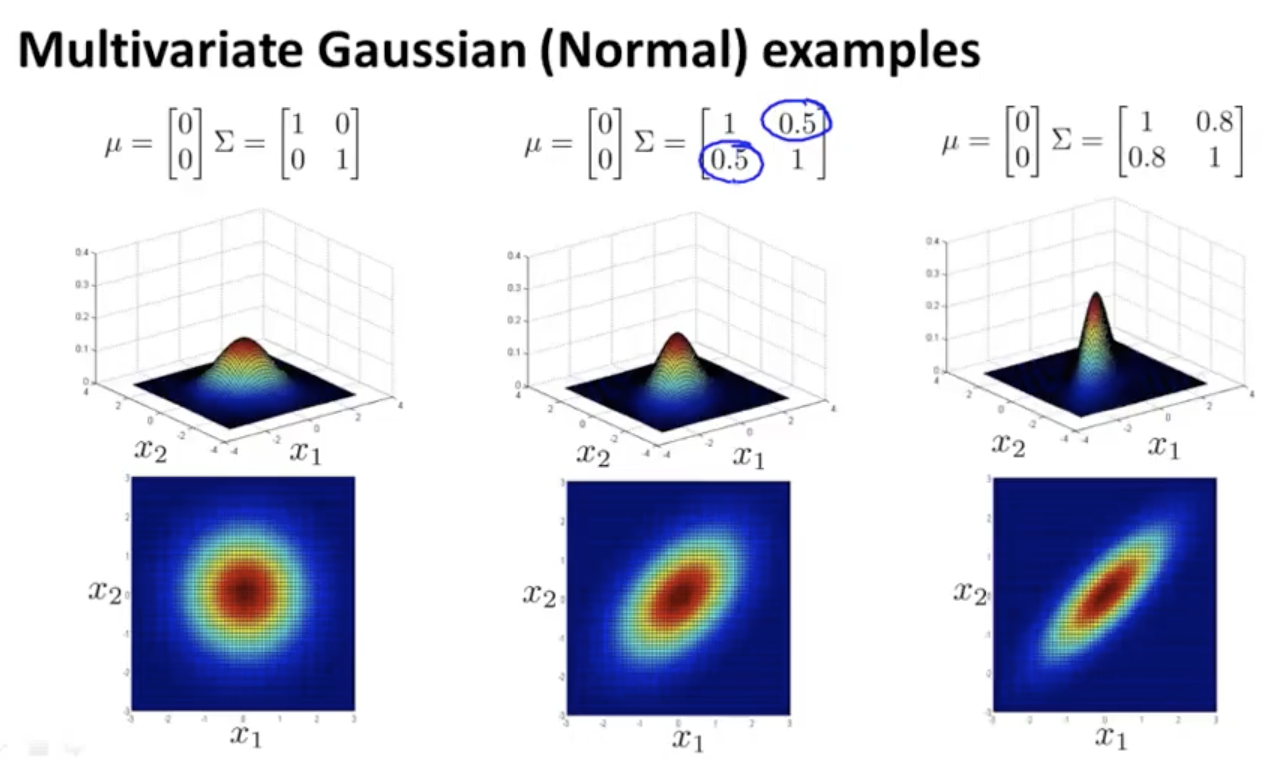
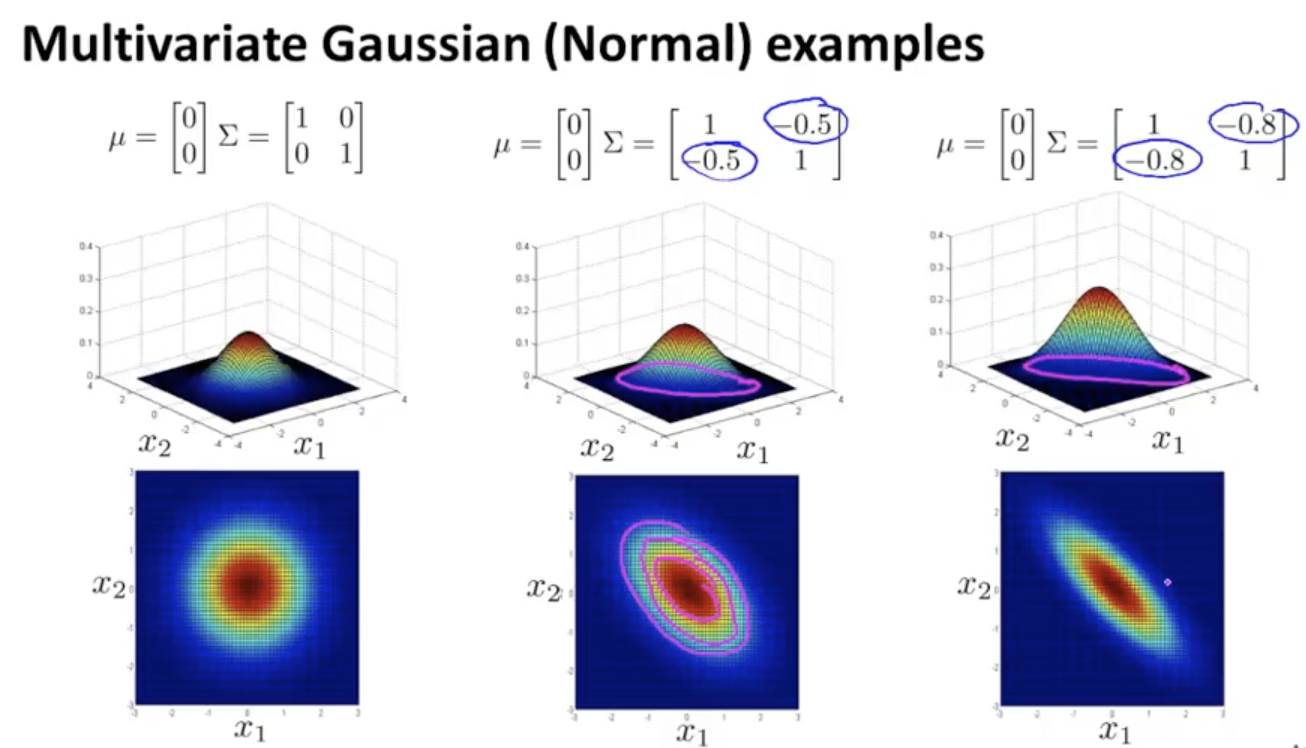
我们可以使用新的概率模型来替换上面式子，同样根据阈值判断是否为异常数据 $P (x) < ε$ 。和之前的公式相比，在数学上一元高斯函数相当于是多元高斯函数的一个特例（协方差矩阵为对角阵）

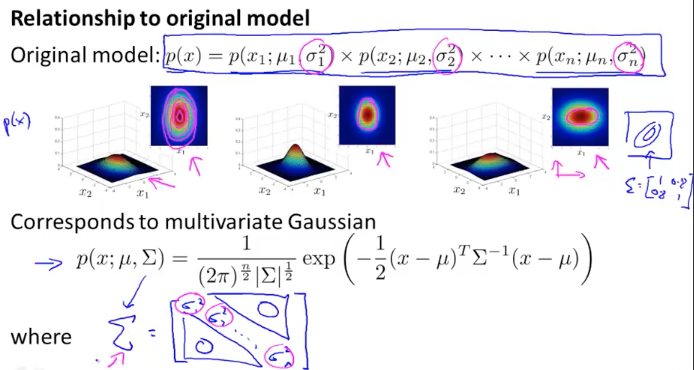
和一元高斯函数相比，多元高斯函数计算复杂度更高，不利于大规模计算以及特征的扩展，当 N 很大时，计算 NxN 的 $\sum$ 矩阵的逆矩阵会很耗时。此外多元高斯模型还要求 m（训练集大小）远大于（至少 10 倍）n（特征数量），否则 $\sum$ 是奇异矩阵，不可逆。而一元模型及时在 m 很小的情况下也可以很好的预测，因此通常情况下我们使用一元模型

如果发现计算多元高斯模型时， $\sum$ 是奇异矩阵不可逆，通常有两种情况，一是 m 小于 n，另一种是包含冗余特征（特征之间线性相关），比如 $x_{1} = x_{2}$ , $x_{3} = x_{4} + x_{5}$ 等

基于内容的推荐系统

假设我们有如下数据，左边是电影名称，右边是用户给电影的评分，假设每部电影有两个特征，分别是爱情片和动作片。我们的目的是根据用户的打分习惯推测出用户未评分的电影分数。

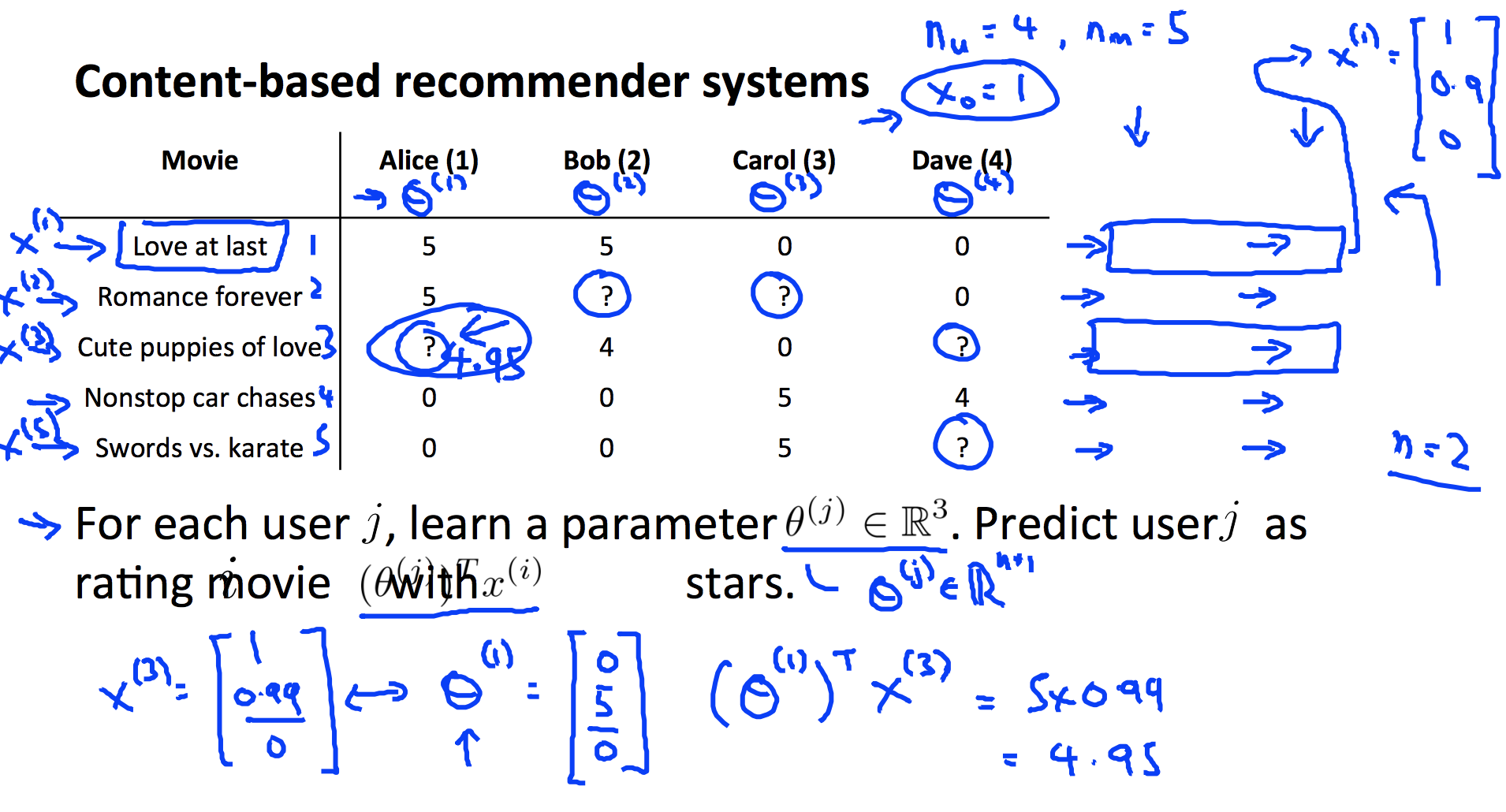
使用 $n_{u}$ 表示用户数量，上面例子中 $N_{u} = 4$
使用 $n_{m}$ 表示电影数量，上面例子中 $N_{m} = 5$
使用 $r (i, j)$ 表示用户 $j$ 是否对电影 $i$ 进行过评分（1 或者 0）
使用 $y^{(i,j)}$ 表示用户 $j$ 对电影 $i$ 的评分
使用 $x^{(i)}$ 表示电影 $i$ 样本特征向量，其中 $x_{0} = 1$ ，以上面例子第一条数据为例： $x^{(1)} = [\begin{matrix} 1 \\ 0.9 \\ 0 \end{matrix}]$
使用 $θ^{(j)}$ 表示用户 $j$ 的参数向量，维度为(N+1)X1
则用户对 $j$ 电影 $i$ 的评分的线性模型为

y^{(i,j)} = (θ^{(j)})^{T} x^{(i)}

上例中，以计算 Alice 对《Cute puppies of love》的评分为例： $x^{(3)} = [\begin{matrix} 1 \\ 0.99 \\ 0 \end{matrix}]$ ，假设 θ 已知， $θ^{(1)} = [\begin{matrix} 0 \\ 5 \\ 0 \end{matrix}]$ ，则 $(θ^{(1)})^{T} x^{(3)} = 5 \* 0.99 = 4.95$ 。抽象出来，对单用户 $j$ 求解 $θ$ 的代价函数以及优化方程为:

min_{θ^{(j)}} \frac{1}{2} \sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)})^{2} + \frac{λ}{2} \sum_{k = 1}^{n} (θ_{k}^{(j)})^{2}

对所有用户，求解 $θ^{(1)}, θ^{(2)}, ..., θ^{n_{u}}$ :

min_{θ^{(1)}, ..., θ^{nu}} \frac{1}{2} \sum_{j = 1}^{nu} \sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)})^{2} + \frac{λ}{2} \sum_{j = 1}^{nu} \sum_{k = 1}^{n} (θ_{k}^{(j)})^{2}

第一个求和项表示对所有用户 j，累加他们所有评过分的电影总和。对上述式子进行梯度下降，求解 θ 值

θ_{k}^{(j)} := θ_{k}^{(j)} - α \sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) x_{k}^{(i)} (for k=0)

θ_{k}^{(j)} := θ_{k}^{(j)} - α (\sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) x_{k}^{(i)} + λ θ_{k}^{(j)}) (for k ≠ 0)

协同过滤(Collaborative Filtering)

协同过滤是一种构建推荐系统的方法，它有一个特点是 feature learning，算法可以自行学习所要使用的特征。还是以上面电影评分为例，对于 $x_{1}, x_{2}$ 两个特征，我们假设有人会告诉我们他们的值，比如某个电影的浪漫指数是多少，动作指数是多少。但是要让每个人都看一遍这些电影然后收集这两个样本的数据是非常耗时的一件事情，有时也是不切实际的，此外，在除了这两个 feature 之外我们还想要获取更多的 feature，从哪里能得到这些 feature 呢。如果我们有一种算法可以在已知个人偏好（θ 值）的前提下，自行推算出 feature 值。如下图所示

假设 Alice, Bob, Carol, Dave 提前告诉了我们他们的个人偏好，即 $θ^{(1)}, θ^{(2)}, θ^{(3)}, θ^{(4)}$ ，根据这些特征向量我们可以推测对于第一部电影 Alice 和 Bob 喜欢，Carol 和 Dave 不喜欢，因此它可能是一部爱情片而不是动作片，即 $x_{1} = 1, x_{2} = 0$ 。数学上看是需要找到 $x^{(1)}$ 使 $(θ^{(1)})^{T} x^{(1)} \approx 5, (θ^{(2)})^{T} x^{(2)} \approx 5, (θ^{(3)})^{T} x^{(3)} \approx 0, (θ^{(4)})^{T} x^{(4)} \approx 0$ 。类似的可以计算出 $x^{(2)}$ , $x^{(3)}$ , $x^{(4)}$ …

因此我们的优化目标为：给定 $θ^{(1)}, θ^{(2)}, ..., θ^{n_{u}}$ ，对单个 feature $x^{(i)}$ 有:

min_{x^{(i)}} \frac{1}{2} \sum_{j:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)})^{2} + \frac{λ}{2} \sum_{k = 1}^{n} (x_{k}^{(i)})^{2}

对多个 feature，给定 $θ^{(1)}, θ^{(2)}, ..., θ^{n_{u}}$ ，求解 $x^{(1)}$ ， $x^{(2)}$ ， $x^{(3)}$ … $x^{(n)}$ 有：

min_{x^{(1)}, ..., x^{(nm)}} \frac{1}{2} \sum_{i = 1}^{nm} \sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)})^{2} + \frac{λ}{2} \sum_{j = 1}^{nm} \sum_{k = 1}^{n} (x_{k}^{(j)})^{2}

使用梯度下降法求解 $x^{(i)}$

x_{k}^{(i)} := x_{k}^{(i)} - α \sum_{j:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) θ_{k}^{(j)} (for k=0)

x_{k}^{(i)} := x_{k}^{(i)} - α (\sum_{j:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) θ_{k}^{(j)} + λ x_{k}^{(i)}) (for k ≠ 0)

对比上一节的公式可以发现，上一节的公式是已知 x 求 θ，这节是已知 θ 求 x，那正确的求解顺序是怎样呢，一种做法是先 Guess 一组 θ 值然后求解 x，再求解 θ 再求解 x，循环直到算法收敛。这种方式可以得到最终的 θ 和 x 值，但是计算过于繁琐和低效，还有一种方式是将两个优化函数联合起来得到一个新的优化函数：

J (x^{(1)}, ..., x^{(nm)}, θ^{(1)}, ..., θ^{(nu)}) = \frac{1}{2} \sum_{(i,j):r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)})^{2} + \frac{λ}{2} \sum_{j = 1}^{nm} \sum_{k = 1}^{n} (x_{k}^{(j)})^{2} + \frac{λ}{2} \sum_{j = 1}^{nu} \sum_{k = 1}^{n} (θ_{k}^{(j)})^{2}

这个式子分别对 x，θ 求导可以还原出上面式子，另外上述式子成立的前提是 x，θ 都为 n 维矩阵，不需要对 $θ_{0}$ 和 $x_{0}$ 做特殊处理。总结一下协同过滤算法：

初始化 $x^{(1)}, ..., x^{(nm)}$ , θ(1) , ... , θ(nu)
</math>为较小的随机数
使用低度下降或其它最优化方法求 $J (x^{(1)}, ..., x^{(nm)}, θ^{(1)}, ..., θ^{(nu)})$ 的最小值，得到最优解 θ 和 x,不需要对 $θ_{0}$ 和 $x_{0}$ 做特殊处理.

x_{k}^{(i)} := x_{k}^{(i)} - α (\sum_{j:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) θ_{k}^{(j)} + λ x_{k}^{(i)})

θ_{k}^{(j)} := θ_{k}^{(j)} - α (\sum_{i:r(i,j)=1} ((θ^{(j)})^{T} x^{(i)} - y^{(i,j)}) x_{k}^{(i)} + λ θ_{k}^{(j)})

对用户的打分计算使用公式 $θ^{T} x$

向量化实现

上述计算也可以通过向量化来表示：

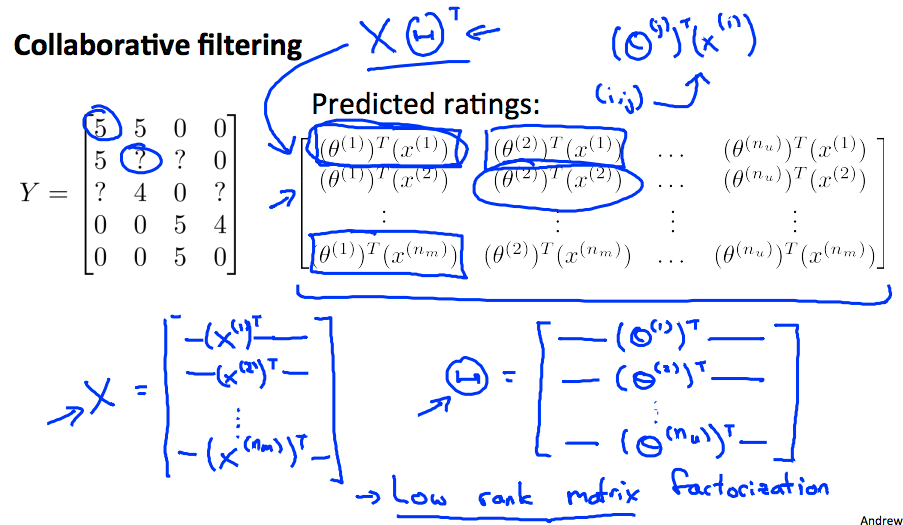
通过对 Y 矩阵的低秩分解求得 θ 和 x。

另一个问题是，我们同样可以通过协同过滤来找到和某个电影相似主题的电影，假设对于电影 $i$ ，我们使用协同过滤的算法得到了一系列特征向量 $x^{(i)}$ ，比如 $x^{(1)} = romance$ , $x^{(2)} = action$ , $x^{(3)} = comdy$ …。怎么找到另一部电影 $j$ 和它类似？可以使用下面式子

Find smallest || x^{(i)} - x^{(j)} ||

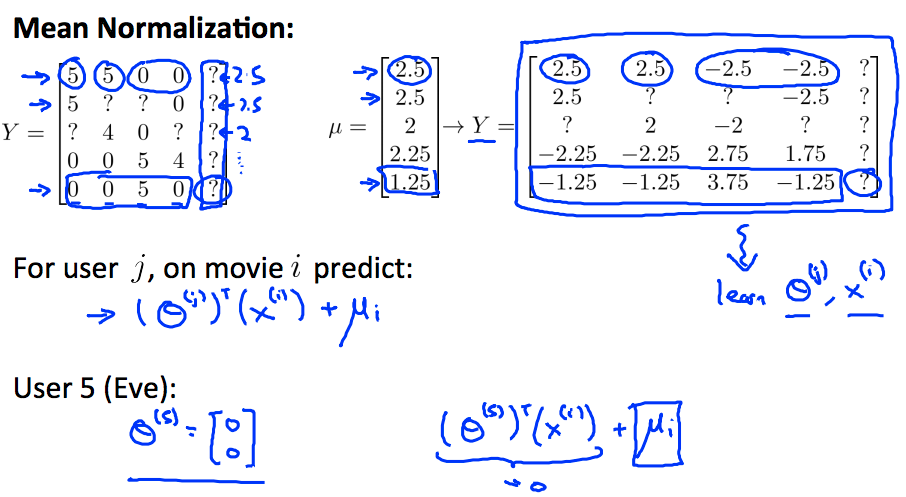
均值归一化

还是上述例子，假设用户 Eve 没有对任何电影评分过，使用上述模型进行计算，将会得到 0 分的结果，如下图所示

解决方式是对于这种情况，使用均值来代替