Learning With Large Datasets

Posted on 2017-11-17 | In Machine Learning , AI

当数据集很大时，进行梯度下降计算会带来较高的计算量。我们需要寻找一些其它的最优化算法来处理大数据的情况

Stochastic gradient descent

以最开始提到的线性回归为例，目标函数为：

h_{θ} (x) = \sum_{j = 0}^{n} θ_{j} x_{j}

代价函数为：

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} {(h_{θ} (x^{(i)}) - y^{(i)})}^{2}

梯度下降公式为：

θ_{j} := θ_{j} - α \frac{1}{m} \sum_{i = 1}^{m} (h_{θ} (x^{(i)}) - y^{(i)}) \cdot x_{j}^{(i)}

上述梯度下降公式也称作“Batch Gradient Descent”它在 $m$ 非常大时（假设 m 为 3 亿，美国人口数量)计算求和的过程非常耗时，它需要把磁盘中所有 m 的数据读入内存，仅仅为了计算一个微分项，而计算机的内存无法一次性存储 3 亿条数据，因此只能批量读入，批量计算，才能完成一次梯度下降的计算。

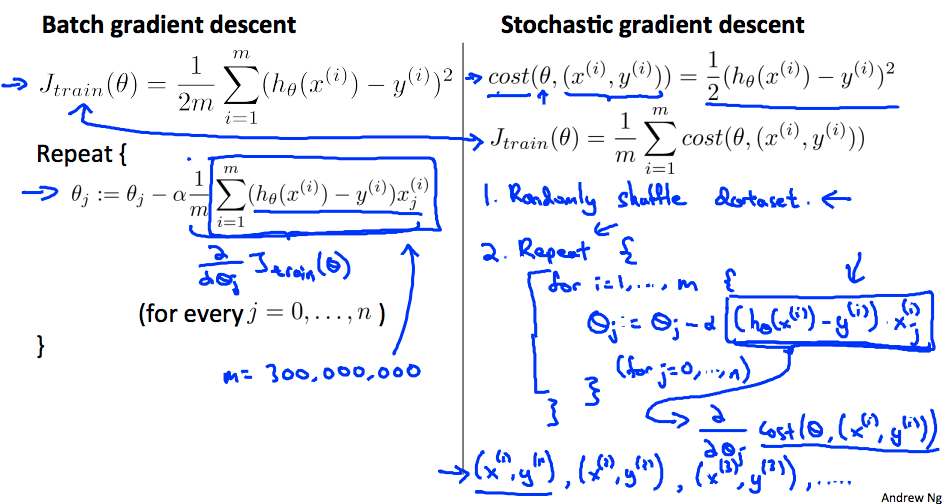
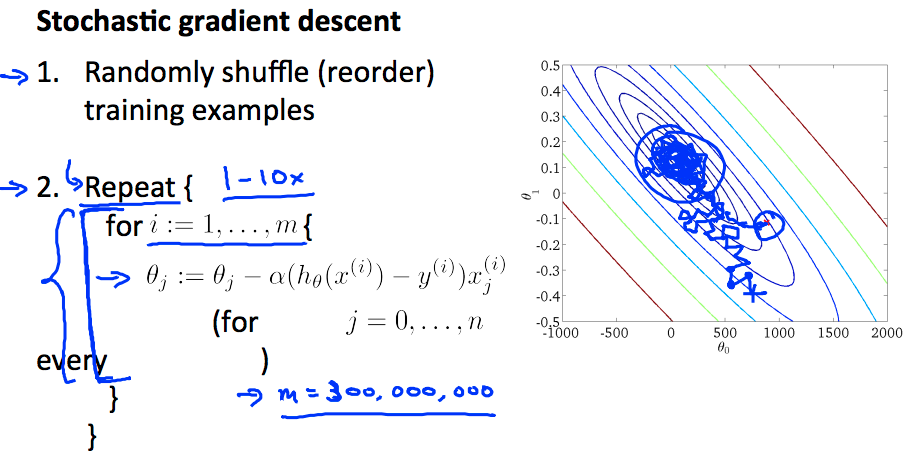
随机梯度下下降法实际上是扫描所有的训练样本，首先是计算第一组样本(x(1),y(1))，对它的代价函数计算一小步的梯度下降，然后把 θ 修改一点使其对第一个训练样本拟合变得好一点。在完成这个内部循环后（先遍历 j 再遍历 i），再转向第二个，第三个样本直到所有样本。外部 Repeat 循环会多次遍历整个训练集，确保算法收敛。需要注意几点：

Repeat 的次数可以选择 1-10，当样本量足够大时，一次内循环就够了
随机梯度下降可以保证参数朝着全局最小值的方向被更新，但无法保证下降的顺序（收敛形式不同）和最终的梯度值不发生变化
随机梯度下降是在靠近全局最小值的区域内徘徊，而不是直接得到全局最小值并停留在那个点上
Learning Rate α 的值通常为常量，如果希望 θ 完全收敛，可以让 α 随时间减小( $α = \frac{const1}{iterationNumber + const2}$ )，通常来说不需要这么做

为了观察算法的学习情况，可以画出随机梯度下降的学习曲线，可能有如下几种情况

Mini-batch gradient descent

Batch gradient descent：每次迭代使用全部 m 个训练样本
Stochasitc gradient descent：每次迭代使用 1 个训练样本
Mini-Batch gradient descent：每次迭代使用 b 个训练样本，b 的取值一般为 2-100

使用 mini-batch 梯度下降的另一个好处是，可以并行处理，将数据分段后，使用向量化进行并行运算