Logistic Regression as a Neural Network
本文部分图片截取自课程视频Nerual Networks and Deep Learning
Logistic Regression Recap
前面机器学习的课程中,我们曾介绍过Logistic Regression的概念,它主要用来解决分类的问题,比如预测结果是True或False的二元分类问题。
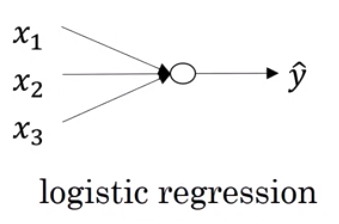
上图所示,我们可以将逻辑回归模型理解为只有一个神经元的神经网络,输入数据通过这个神经元后,得到一组分类结果。如果我们将x,y都用矩阵表示,则公式为
\[\hat{y} = \sigma(w^Tx + b)\]其中$\hat{y}$, $x$, $w$ 和 $b$ 皆为矩阵,$\sigma$为sigmoid函数,定义为$\sigma(z) = \frac{1}{1+e^{-z}}$。我们假设第$i$组训练样本用向量$x^{(i)}$表示,则$x^{(i)}$是$nx1$的(注意是n行1列),那么假设一共有$m$组训练样本,则样本矩阵$X$表示为
\[X= \begin{bmatrix} . & . & . & . & . & . & . \\ . & . & . & . & . & . & . \\ x^{(1)} & x^{(2)} & x^{(3)} & . & . & . & x^{(m)} \\ . & . & . & . & . & . & . \\ . & . & . & . & . & . & . \\ \end{bmatrix}\]类似的$w$是一个nx1的向量,则$w^Tx$是1xm的, 对应的常数项$b$也是1xm的矩阵。对任意第$i$个训练样本,有
对所有训练集则可以使用矩阵运算来表示
\[\begin{bmatrix} z^{(1)} & z^{(2)} & . & . & . &z^{(m)} \end{bmatrix} = w^{T}X + \begin{bmatrix} b_1 & b_2 & . & . & . &b_n \end{bmatrix}\]对任意训练集$i$,另$a^{(i)} = \sigma(z^{(i)})$,则最后的预测结果$\hat{y}$可以表示为
\[\hat{y} = \begin{bmatrix} a^{(1)} & a^{(2)} & . & . & . &a^{(m)} \end{bmatrix}\]因此预测结果$\hat{y}$为1xm的向量
Cost function
对于某一组训练集可知其cross-entropy loss函数为
\[L(\hat(y),y) = - (y\log{\hat{y}}) - (1-y)\log{(1-\hat{y})}\]然后我们对所有$m$组训练集都计算Loss函数,之后再求平均,则可以得到Cost function
\[J(w,b) = \frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) = -\frac{1}{m}\sum_{i=1}^{m}[(y^{(i)}\log{\hat{y}^{(i)}}) + (1-y^{(i)})\log{(1-\hat{y}^{(i)})} ]\]Gradient Descent
有了Cost funciton之后,我们就可以使用梯度下降来求解$w$和$b$,使$J(w,b)$最小。梯度下降的计算方式如下
\[w := w - \alpha\frac{dJ(w,b)}{dw} \\ b := b - \alpha\frac{dJ(w,b)}{db}\]上述式子通过不断的对$w$和$b$进行求偏导,最终使其收敛为一个稳定的值,其中$\alpha$为Learning Rate,用来控制梯度下降的幅度。在后面的Python代码中,使用dw表示 $\frac{dJ(w,b)}{dw}$,db表示$\frac{dJ(w,b)}{db}$,以此类推。
Computation Graph
虽然我们有了上面的算式,但如何有效的计算它是我们接下来要讨论的问题,这里我们介绍一种使用Computation Graph的思路,所谓的Computation Graph的概念,基本思想是将每一步运算都用一个节点表示,然后将这些节点串联起来得到一个Graph,举例来说,假设有一个函数为
\[J(a,b,c) = 3(a+bc)\]我们另
- $u = bc$
- $v = a+u$
- $J = 3v$
则该算式的Computation Graph可以表示如下
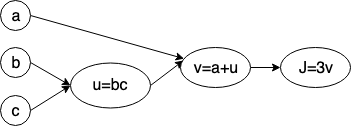
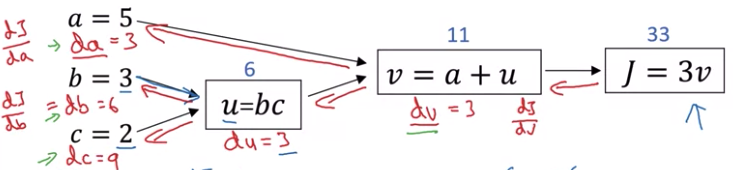
接下来我们要思考如何对Graph中的每一项进行求导,这将是后面计算神经网络backpropagation的基础。显然如果有微积分基础的话,这并不难
- $\frac{dJ}{dv} = 3$
- $\frac{dJ}{du} = \frac{dJ}{dv} \times \frac{dv}{du} = 3 \times 1 = 3$
- $\frac{dJ}{da} = \frac{dJ}{dv} \times \frac{dv}{da} = 3 \times 1 = 3$
- $\frac{dJ}{db} = \frac{dJ}{dv} \times \frac{dv}{du} \times \frac{du}{db} = 3 \times 1 \times c = 3c$
- $\frac{dJ}{dc} = \frac{dJ}{dv} \times \frac{dv}{du} \times \frac{du}{dc} = 3 \times 1 \times b = 3b$
在接下来的代码中,我们需要表示上面的每个导数值,其表示方式为
\[\frac{dFinalOutputVar}{dvar}\]这种写法太过冗余,因此,如果想表示$\frac{dJ}{da}$,在代码中可直接写成da,其余同理,计算这些变量到数值的过程,可类比于神经网络的backpropagation
Loss Function
理解了Computation Graph,我们回到算梯度下降上来,我们先看一种简单的情况,假设我们只有一组训练样本,该样本中只有两个feature,$x_1$和$x_2$,我们用$w_1$和$w_2$表示两个feature对应的权重,则预测的model可以表示为
\[\hat{y} = \sigma(z) = \sigma(w_1x_1 + w_2x_2 + b) \\\]为了求解$w_1$和$w_2$,结合上面给出的Loss函数,得到生成的Computation Graph如下
注意这里使用的是Loss函数,而不是Cost函数,因为当前case为单一的样本,不涉及到所有的样本集
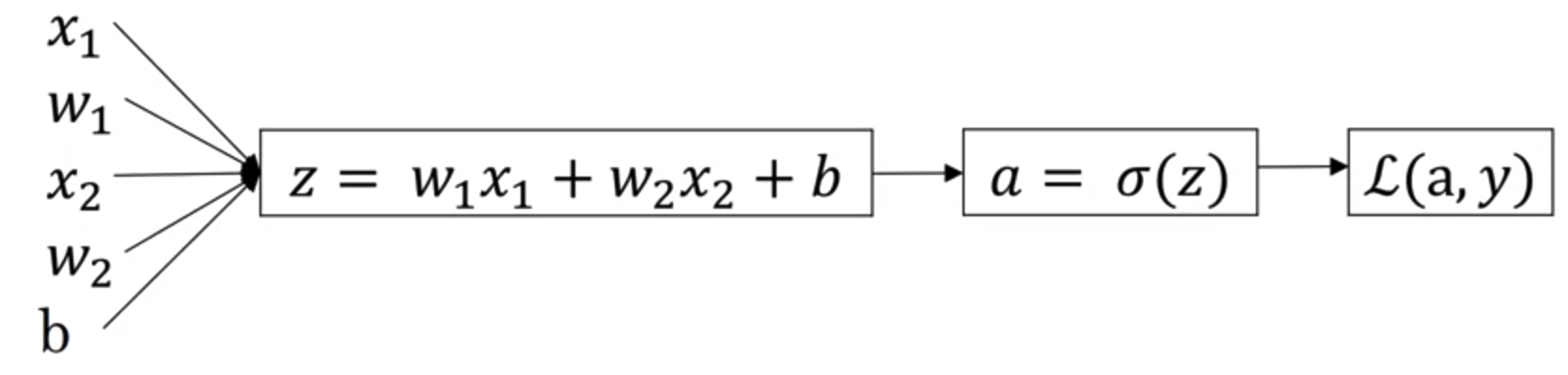
为了使Loss函数的值最小,我们需要使用梯度下降来计算$w_1$,$w_2$和$b$
\[w_1 := w_1 - \alpha\frac{dL(a,y)}{dw_1} \\ w_2 := w_2 - \alpha\frac{dL(a,y)}{dw_2} \\ b := b - \alpha\frac{dL(a,y)}{db}\]接下来利用前面提到的求偏导的方式,一步步反向计算得到 $w_1$ 和 $w_2$的最终值,如下图所示
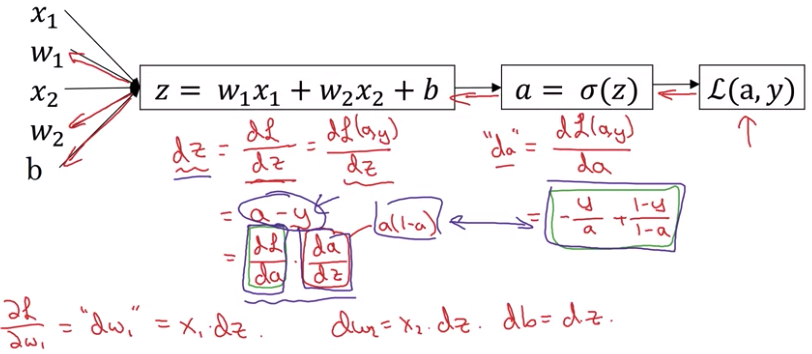
- $da = \frac {dL(a,y)} {da} = - \frac{y}{a} + \frac{1-y}{1-a}$
- $dz = \frac {dL(a,y)} {dz} = \frac {dL(a,y)}{da} \times \frac {da}{dz} = a-y$
- $dw_1 = \frac {dL(a,y)} {dw_1} = x_1 \times dz$
- $dw_2 = \frac {dL(a,y)} {dw_2} = x_2 \times dz$
Cost Function
接着我们可以考虑使用上述方法来计算逻辑回归的cost function,如前所述,对于任意一组的训练集,我们用$x^{(i)}$表示第i个样本, 每个样本$x^{(i)}$包含$n$个feature,则$x^{(i)}$是n x 1的,每组样本的预测结果用$\hat{y}^{(i)}$或$a^{(i)}$表示,假设整个训练集有$m$组样本,则对于cost function可以表示为
可以看到,cost函数只是loss函数的平均值,现在我们假设$n=2$,则每组样本都有两个feature,对应的$w^{(i)}$是$2\times1$的,即[w1,w2],因此对$dw_1^{(i)}$的计算只需要循环$m$次累加$\frac{d(a^{(i)}, y^{(i)})}{dw_1}$,然后求平均即可,$dw_2^{(i)}$同理
伪代码如下
J=0, dw1=0, dw2=0, db=0
for i=1 to m
z[i] = w.tx[i] + b
a[i] = sigmoid(z[i])
J += -y[i]*log(a[i]) + (1-y[i])log(1-a[i])
dz[i] = a[i] - y[i]
for j=1 to n
dw[j] += x[i][j] * dz[i] #第i组样本的第j个feature
db += dz[i]
# if n = 2
#dw1 += x[i][1] * dz[i]
#dw2 += x[i][2] * dz[i]
dw1 = dw1 / m
dw2 = dw2 / m
db = db / m
w1 = w1 - alpha*dw1
w2 = w2 - alpha*dw2
b = b - alpha*db
上面代码展示了某一次梯度下降的计算过程
Resources
附录:Vectorization using Numpy
由于深度学习涉及大量的矩阵间的数值计算,而且数据量有很大,使用for计算时间成本太高。Vectorization是用来取代for循环的一种针对矩阵数值计算的计算方式,其底层可以通过GPU或者CPU(SIMD)的并行指令集来实现。不少数值计算库都有相应的实现,比如Python的Numpy,C++的Eigen等。
比如我们想要计算$z = w^Tx+b$,我们假设$x$和$w$都是nx1的向量,我们使用Python来对比下两种计算方式的差别
#for loop
z = 0
for i in range(1,n):
z += w[i] * x[i]
z+=b
# use numpy
# vectorized version of doing
# matrix multiplications
z = np.dot(w.T,x)+b
numpy数组的另一个特点是可以做element-wise的矩阵运算,这样让我们避开了for循环的使用
a = np.ones([1,2]) #[1,1]
a = a*2 #[2,2]
接下来我们可以使用numpy重新实现以下上一节计算dw代码的for循环部分
J=0,db=0
dw = np.zeros([n,1])
for i=1 to m
#z是1xm的
#x是nxm的
z[i] = w.tx[i] + b
a[i] = sigmoid(z[i])
J += -y[i]*log(a[i]) + (1-y[i])log(1-a[i])
dz[i] = a[i] - y[i]
# for j=1 to n
# dw[j] += x[i][j] * dz[i] #第i组样本的第j个feature
dw += x[i]*dz[i]
db += dz[i]
dw = dw/m
在前面第一节计算矩阵$Z$的式子上
\[Z= \begin{bmatrix} z^{(1)} & z^{(2)} & . & . & . &z^{(m)} \end{bmatrix} = w^{T}X + \begin{bmatrix} b_1 & b_2 & . & . & . &b_n \end{bmatrix}\]如果使用numpy表示,则只需要一行代码
Z = np.dot(w.T,X) + b #b is a 1x1 number
在通过Loss函数计算w值时,我们曾给出过下面式子
\[dz^{(1)} = a^{(1)} - y^{(1)} \\ dz^{(2)} = a^{(2)} - y^{(2)} \\ ... \\ dz^{(i)} = a^{(i)} - y^{(i)} \\\]训练集共有$m$,则$dz$的矩阵(1xm)表示为
另 $A = [a^{(i)}…a^{(m)}]$, $Y = [y^{(i)}…y^{(m)}]$,则
\[dZ = A - Y = [a^{(1)} - y^{(1)}, a^{(2)} - y^{(2)}, ... , a^{(m)} - y^{(m)}]\]在前面求解$dw$的代码中,我们虽然将$dw$向量化后减少了一重循环,但最外层还有一个[1,m]的for循环,接下来我们也可以将这个for循环向量化。
我们的目的是求解$dw$和$d$`,其中$db$为
\[db = \frac{1}{m}\sum_{i=1}^{m}dz^{(i)}\]上述式子可以用numpy一行表示 db = 1/m * np.sum(dZ),对于$dw$,有
