Convolutional Neural Networks

Posted on 2018-03-20 | In AI , Machine Learning , Deep Learning

文中部分图片截取自课程视频Nerual Networks and Deep Learning

CNN是深度学习中一种处理图像的神经网络，可以用来做图像的分类，segmentation，目标检测等等。其工作原理可简单概括为通过神经网络对图片特征的提取来达到我们想要的结果，相比于Full Connected网络，CNN需要学习的参数显著变少，相当于对图像进行了压缩。

卷积运算

CNN对图片特征的提取是基于卷积运算，由于图片中的像素点在空域上是离散的，因此准确的说是离散卷积运算。如果熟悉信号处理可知，卷积运算在频域上是一种滤波，比如图片的边缘包含大量的高频信息，我们可以设计一个高频滤波器对图片进行卷积，这样只有图片中的高频分量才能通过滤波器，即过滤出了图片的边缘。在空域上，卷积运算是一种加权求和的运算。其具体过程为让一个卷积核（卷积核）依次滑过图片中的所有区域，如下图所示

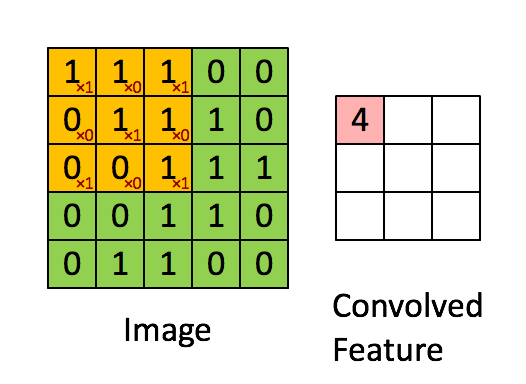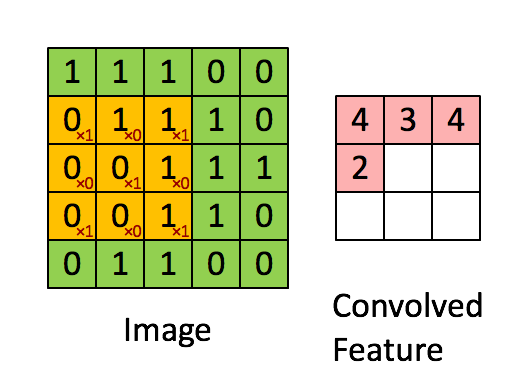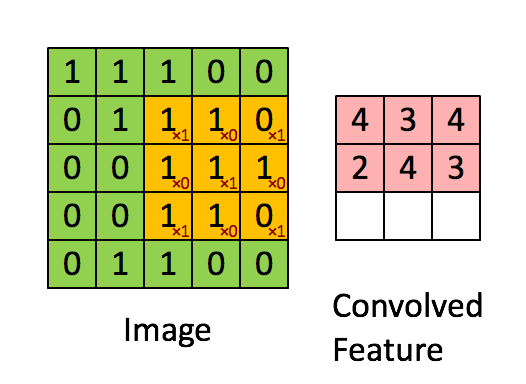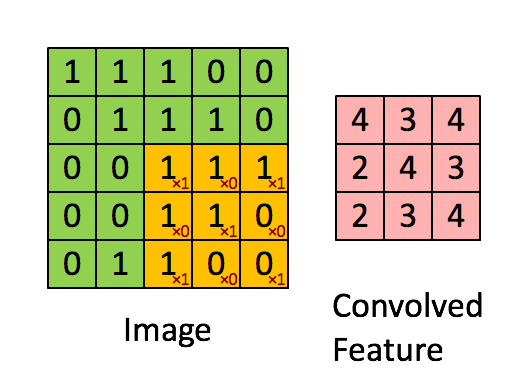
假如我们有一副灰度图片，我们可以选取两个固定的卷积核，分别对图像进行水平和竖直的卷积操作（高通滤波）来提取边缘，结果如下图所示

我们假设图片的大小是nxn的，卷积核的大小是fxf的，那么滤波后图片的大小为

$(n-f+1) \times (n-f+1)$

如果熟悉图像处理算法，可知边缘检测的算子有很多种，比如Sobel，拉普拉斯等。但是这些算子的值都是根据经验来确定的，比如Sobel的算子的值为

$\begin{bmatrix} 1 & 0 & 1 \\ 2 & 0 & -3 \\ 1 & 0 & -1 \\ \end{bmatrix}$

但基于传统图像处理算法对边缘的提取效果并不是最佳的，与其根据经验值来确定卷积核中的值，CNN可以通过训练来找到最佳的卷积核，这也是CNN所要最终解决的问题，即通过训练找到各式各样的卷积核来帮我们完成最终的任务。

Padding

从上面边缘检测的例子中可以看出，每当图片完成一次卷积运算后，它的大小会变小；另外，对于图片中边缘的像素点，只会经过一次的卷积运算，而对于位于图中中心位置的点，则可能经过多次的卷积运算，因此卷积运算对于图片边缘的点并不能有效的运用起来。

为了解决这两个问题，我们可以给输入的图片增加一圈padding，以上面6x6的图片为例，如果我们在图片周围各加一个像素的padding，那么6x6的图片，将会变成8x8，经过卷积运算后的图片尺寸依旧是 8-3+1 = 6x6。我们另$p$为padding的像素数，则卷积后的图片尺寸为

$(n+2p-f+1) \times (n+2p-f+1)$

在CNN中，我们称Valid为没有padding的卷积运算，称Same为有padding的卷积运算，卷积后的尺寸和原图片相同，此时要求

$p = \frac{f-1}{2}$

在计算机视觉中，f通常为奇数。

Strided Convolutions

在前面例子中，卷积核滑过图片时的步长为1，我们也可以改变卷积核滑动的步长，如下图中，卷积核滑动的步长为2

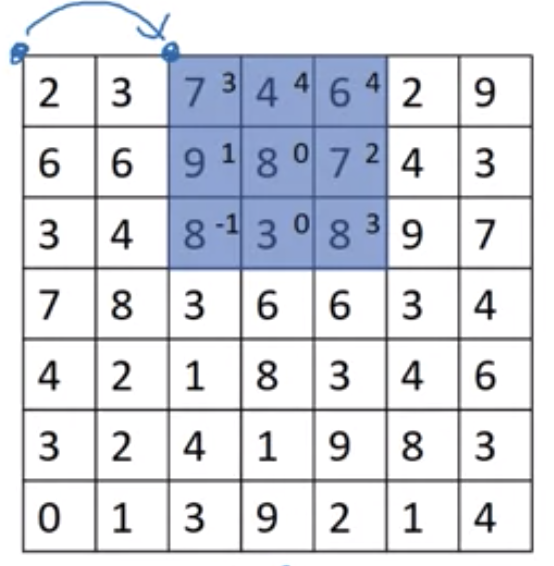
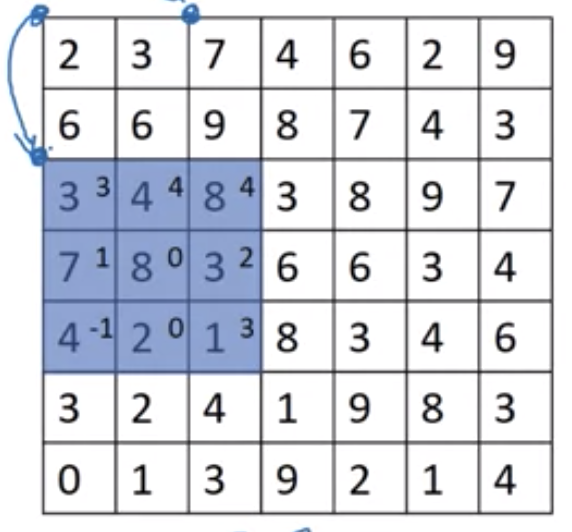
上图中，一个7x7的图片和一个3x3的卷积核，按照步长为2进行卷积运算，得到的图片大小为3x3。计算方法为

$\lfloor{\frac{n+2p-f}{stride} + 1}\rfloor \times \lfloor{\frac{n+2p-f}{stride} + 1}\rfloor$

三维卷积运算

在前面的例子中，我们介绍了二维灰度图片的卷积运算，我们可以将原理推广到三维的RGB图片上，对于RGB图片的卷积运算，我们可以用下图表示

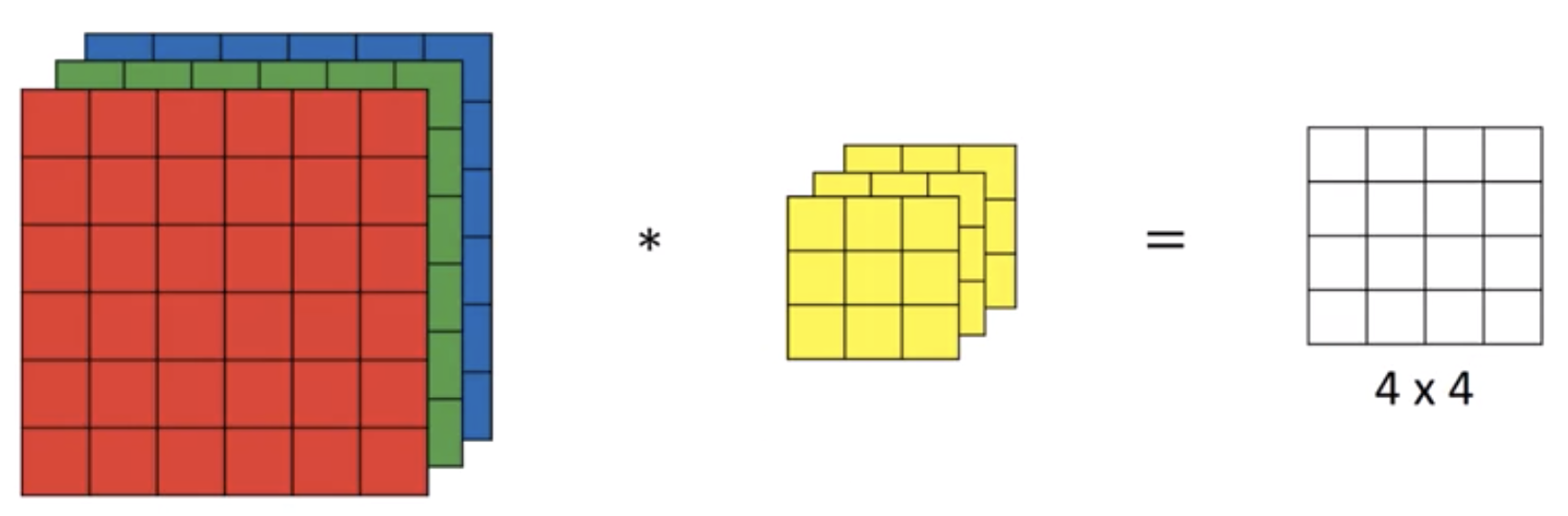
此时我们的输入图片变成了6x6x3的矩阵，表示有三张RGB的二维图片，内存中的排列方式为

r r r ... r
r r r ... r
... ... ...
r r r ... r
g g g ... g
g g g ... g
... ... ...
g g g ... g
b b b ... b
b b b ... b
... ... ...
b b b ... b

值得注意的是，对于图片矩阵，6x6x3的含义和3x6x6的含义并不相同，后者表示的矩阵为

rgb rgb rgb ... rgb
rgb rgb rgb ... rgb
... ... ... ... rgb
rgb rgb rgb ... rgb

同样对于卷积核，也是一个3x3x3的矩阵，对应RGB三个通道。整个卷积运算的过程为RGB三通道图片分别和对应的卷积核进行卷积操作，将结果填充到一个4x4的矩阵中。

注意到，上图中我们只考虑了一种情况，即一张RGB图片和一个卷积核进行卷积得到一个4x4的矩阵，这个卷积核可以是竖直边缘检测的卷积核，那么得到的4x4矩阵则是图片的竖直边缘特征。如果我们要同时提取图片的竖直和水平边缘则需要让图片和另一个卷积核进行卷积，得到另一个4x4的矩阵，那么最终的结果将是一个4x4x2的矩阵，如下图所示

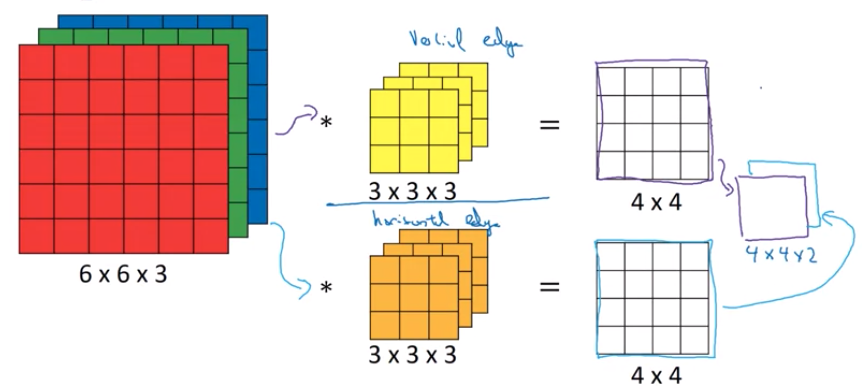
这个视频更好的展示上述卷积计算的过程

小结一下，对于彩色图片的卷积操作，一张$n \times n \times n_c$的图片和$n_c^{‘}$个$f \times f \times n_c$个卷积核做卷积得到的输出为

$(n-f+1) \times (n-f+1) \times n_c^{'}$

其中$n_c^{‘}$为卷积核的个数

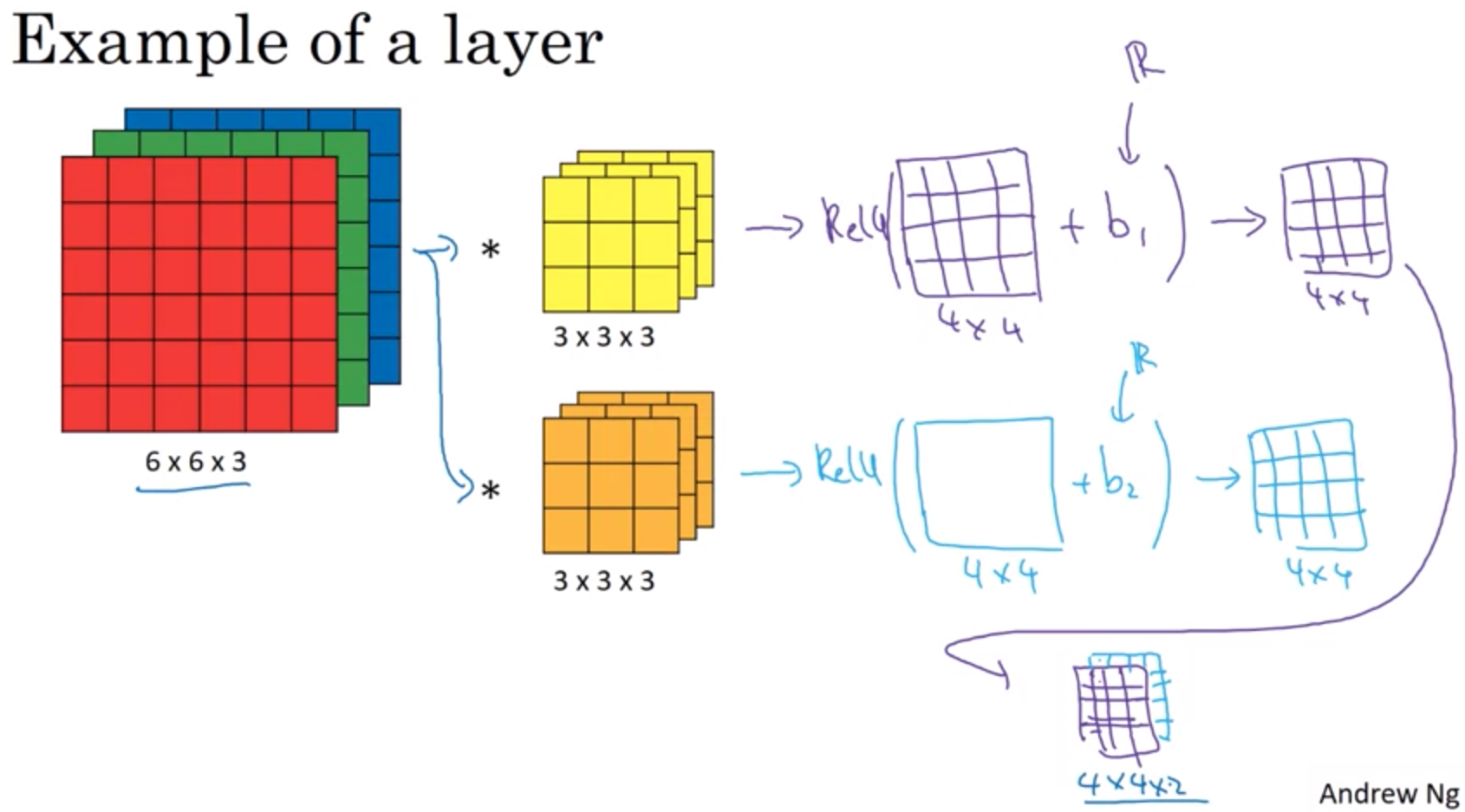
如上图中是一个一层的CNN，其中hidden layer包含两个4x4的节点$a_i$。回忆前面神经网络的概念，对于单层的神经网络，输出可用下面式子表示

$z^{[1]} = W^{[1]}a^{[0]} + b^{[1]} \\ a^{[0]} = g(z^{[1]}) \\$

对应到CNN中，$a^{[0]}$是我们输入的图片，大小为6x6x3，两个卷积核类比于$W^[1]$矩阵，则$W^{[1]}a^{[0]}$类比于$a^{[0]} * W^{[1]}$得到的输出为一个4x4的矩阵，接下来让该矩阵中的各项加上bias，即$b1$，$b2$，再非线性函数$Relu$对其求值，则可得到$a^{[1]}$

如果layer $l$是一个convolution layer，另

$f^{[l]}$ = filter size
$p^{[l]}$ = padding
$s^{[l]}$ = stride
$n_C^{[l]}$ = number of filters

则layer ${l}$的input的size为

$n_H^{[l-1]} \times n_W^{[l-1]} \times n_C^{[l-1]}$

output的size为

$n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$

其中，$n_H^{[l]}$ 和 $n_W^{[l]}$的size计算公式前面曾提到过

$n_H^{[l]} = \lfloor{\frac{n^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}} + 1}\rfloor$

每个Fileter的size为

$f^{[l]} \times f^{[l]} \times n_C^{[l-1]}$

Hidden Layer中每个Activation unit $A^{[l]}$的size为，其中m为batch数量

$m \times n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$

Weights $W^{[l]}$的size为

$f^{[l]} \times f^{[l]} \times n_C^{[l-1]} \times n_C^{[l]}$

Bias $b^{[l]}$的size为 $n_C^{[l]}$

Pooling

Pooling是用来对输入矩阵进行优化的一种方法。举例来说，下图是对一个4x4的矩阵进行max pooling，得到一个2x2的矩阵

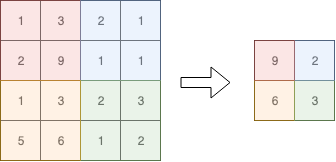
上图中，max-pooling的两个参数 - $stride$为2，$f$为2，对于多维矩阵同理

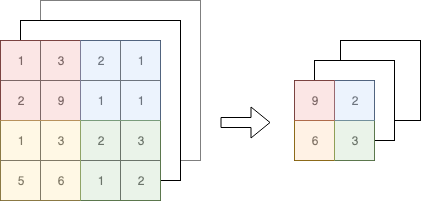
注意，Pooling用到的这两个参数是经验值，并非通过backprop求得。

总结一下，如果Pooling layer的输入为 $n_H \times n_W \times n_C$，则输出的size为

$\lfloor{\frac{n_H-f}{stride} + 1}\rfloor \times \lfloor{\frac{n_W-f}{stride} + 1}\rfloor \times n_C$

一个完整的卷积神经网络

最后我们来看一个完整的卷积神经网络，一般来说，一个卷积神经网络有下面几种layer

Convolution
Pooling
Fully connected

如下图是一个LeNet-5的卷积神经网路

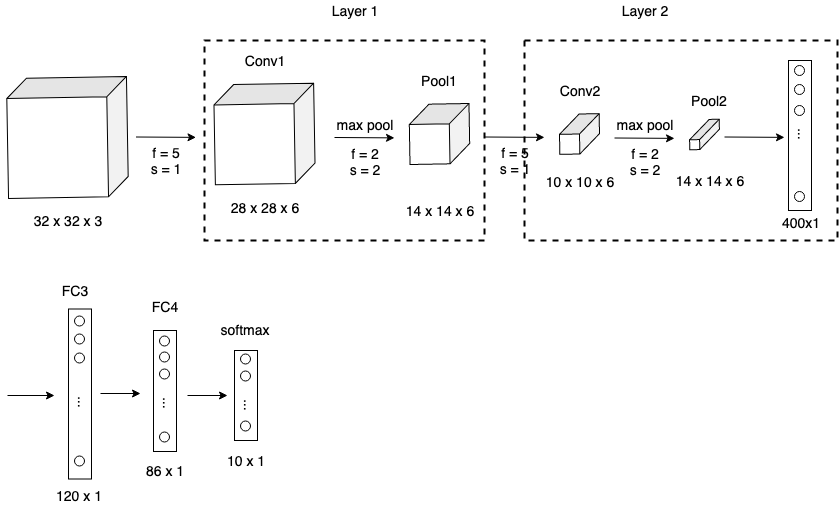
该神经网络后面几层为Fully connected layer。对于卷积神经网络一个比较常见的pattern是conv layer后面追加pooling layer，并且最后几层为FC，然后是一个softmax做分类。我们可以详细的看一下每一层的数据

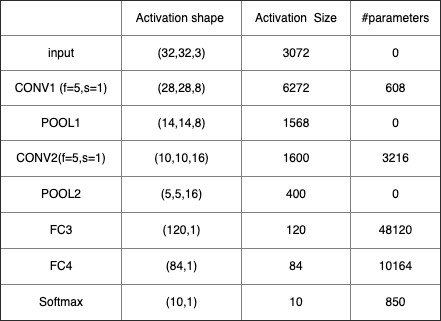
可以看出，hidden layer的Activation units的shape和size都是逐层减少的。看到这里不禁有人会问，这种卷积神经网络和之前介绍的普通神经网络或者FC神经网络相比有什么好处呢？好处大概有这么两点

Parameter Sharing

相比于直接使用FC，使用conv layer的好处在于需要学习的weight数量会显著减少，比如还是上面的例子，如果使用FC，那么第二层的weight数量为 3072 * 4704，这个训练量是巨大的。而如果使用conv layer，待训练的数量只有156个。其背后的原因在于卷积运算的卷积核（feature detector）是可以复用的，比如在图片左上角检测边缘的卷积核对于图片右下角的边缘也适用。因此我们只需要一个卷积核就可滑过整张图片。

Sparsity of connections

对于卷积后图片上每一点的值只和原图中某个局部的区域有关，区域的的大小取决于卷积核的大小，和其余的点无关。而对于FC来说，它将图片从二维矩阵转成了一维向量，对于像素点来说，相当于丢失了位置信息。取而代之的是每个点的计算都和前一个layer的所有点有关联，因此计算效率会大大降低