Neural Style Transfer
Neural Style Transfer
所谓Netural Style Transfer是指将一幅图片的style信息提取出来并应用到另一幅图片的content上,从而合成一副同时具备两幅图片特征的新图片。如下图所示

接下来的问题便是
- 如何提取content image中的content
- 如何提取style image中的style
- 如何提取出的content和style重新组合起来
Content Representation
参考文献[1]的论文中提到,使用卷积神经网络来帮我们提取content。这里我们要先重新回顾一下前面的内容,以图像分类为例,一个卷积神经网络可以分为两部分,前一部分是由conv2d和pooling组成的卷积层,其作用是提取图片中的特征。后一部分是由FC层和Softmax组成的分类层,其作用是将图片的特征flatten成一维向量并映射到某个具体的类别上。
而对于提取特征来说,我们并不需要后面的FC层,只需要保留前面的卷积层即可。论文中使用VGG19,如下图所示
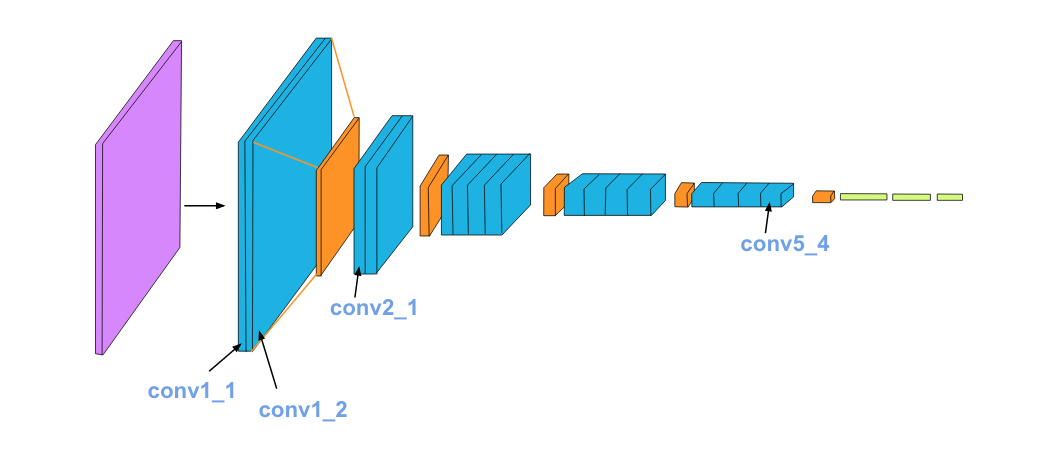
虽然我们保留了卷积层,但我们还要知道图片通过每个卷积层之后的输出,也就是说各卷积核到底在提取图片的哪些特征,阅读参考文献[2,3]可知,随着卷积网络的加深,卷积层提取的特征粒度将越来越大,比如前几层的卷积层可识别图片的边缘,颜色等,随着网络的加深,后面几层则可以识别人脸,身体等大型特征,如下图所示

在论文中,作者观察了VGG19的
conv1_2,conv2_2,conv3_2,conv4_2和conv5_2这几层的输出,发现使用conv4_2可以很好的重建原图的特征。
接下来我们要做的便是根据某输出层(例如conv4_2)的图片来重建一张新的图片,新的图片需要具备原图的重要特征。我们首先创建一张目标图片(可以直接用原图)并让其通过某层(例如conv4_2),结果用$G$表示。接着将原图也通过该层,输出用$C$表示,最后来我们计算$G$和$C$的element-wise的差值,使用下面的式子
上述式子的对$G$的偏导为
\[\begin{equation} \frac{\partial L_{content}(C,G)}{\partial G_{i,j}^{[l]}} = \left\{ \begin{array}{rcl} {(G^{[l]} - C^{[l]})}_{i,j} & & {G_{i,j}^{[l]} > 0} \\ 0 & & {G_{i,j}^{[l]} < 0} \end{array} \right. \end{equation}\]有了上面的loss函数,我们便可以用梯度下降法使$L_{content}最小,$并最终确定$G$的值
Style Representation
这一节我们来讨论如何表示图片中的Style信息。论文中指出图片的style信息可以用feature之间的相关性表示,例如我们有一个张image,通过一个卷积层$l$后得到了一个[4,4,8]feature矩阵,则style信息就可以用这8个[4,4]矩阵的相关性来表示。
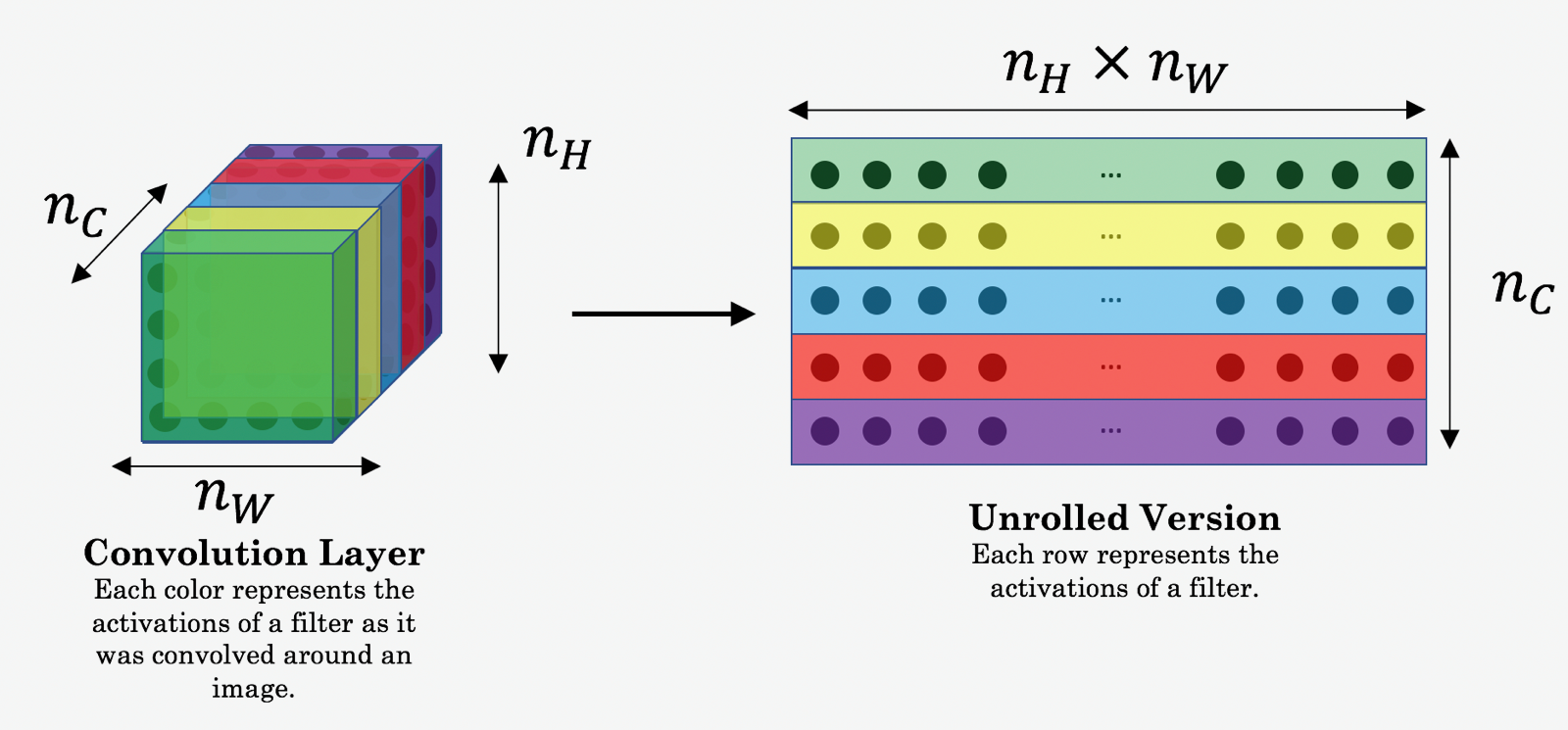

具体来说,假如我们的feature矩阵如左图所示,其中前两层为例(绿色和黄色)分别对应右图的两个红色框的feature矩阵,则所谓的相关性可表示为当第一层出现“竖条”这样的图案时,第二层的颜色是“橘黄色”。
相关性在数学上可以用Gram矩阵表示,我们用$i$,$j$,$k$分别表示$n_i$,$n_j$和$n_c$,用$l$表示第某$l$层,用$a_{i,j,k}^{[l]}$表示feature矩阵,$G,S$分别表示目标图片和Style图片,则$G^{[l]}$的定义如下
\[G_{k,k^{'}}^{[l](S)} = \sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{i,j,k}^{[l](S)}a_{i,j,k^{'}}^{[l](S)} \\ G_{k,k^{'}}^{[l](G)} = \sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{i,j,k}^{[l](G)}a_{i,j,k^{'}}^{[l](G)}\]实际编程中$G^{[l]}$可以用$AA^{T}$来计算,其size为$(n_c^[l],n_c^[l])$。是以上面两个[4,4,8]feature矩阵为例,首先将它们转化为两个[16,8]的二维矩阵,然后计算$AA^T$,则得到的G矩阵为[8,8],如下图所示
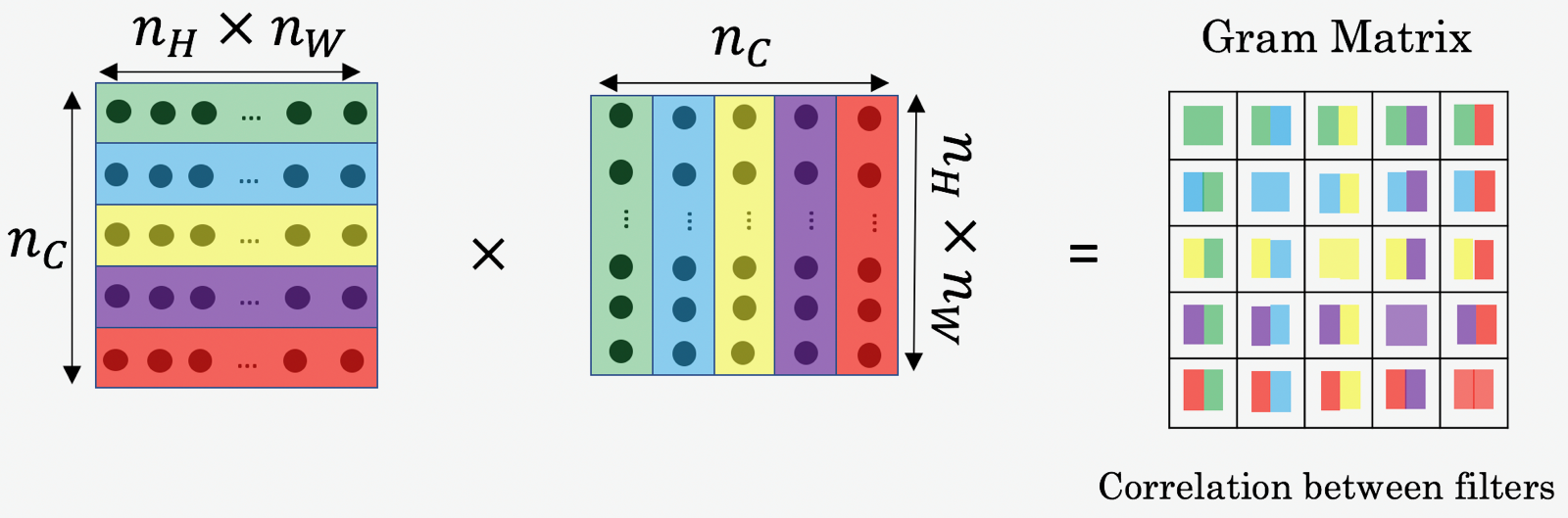
有了gram矩阵的定义,我们就可以算$S$和$G$在$l$层的loss函数
\[J_{style}^{[l]} (S,G) = \left\|G_{k,k^{'}}^{[l](S)} - G_{k,k^{'}}^{[l](G)} \right\|^2 = \frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2}\sum_{k}^{n_C}\sum_{k^{'}}^{n_C}(G_{k,k^{'}}^{[l](S)}-G_{k,k^{'}}^{[l](G)})^2 \\\]将所有layer叠加,总的loss函数为
\[J_{style}(S,G) = \sum_{l=0}^{L}\omega^{[l]}J_{style}^{[l]} (S,G)\]其中$\omega$的取值在[0,1]之间,由于上述式子对$G$可微,我们同样可以用梯度下降找到loss函数的最小值,从而确定$G$
Cost函数
有了前面两个loss函数,接下来我们只需要将它们Combine起来即可,其中$\alpha$和$\beta$用来控制style和content的权重
\[L_{total} = \alpha J_{content}(S,G) + \beta J_{style}(S,G) \\ G := G - \alpha \frac{\partial L_{total}} {\partial G}\]我们接下来要做的就是通过梯度下降不断迭代,更新$G$中的像素点,整个过程如下图所示
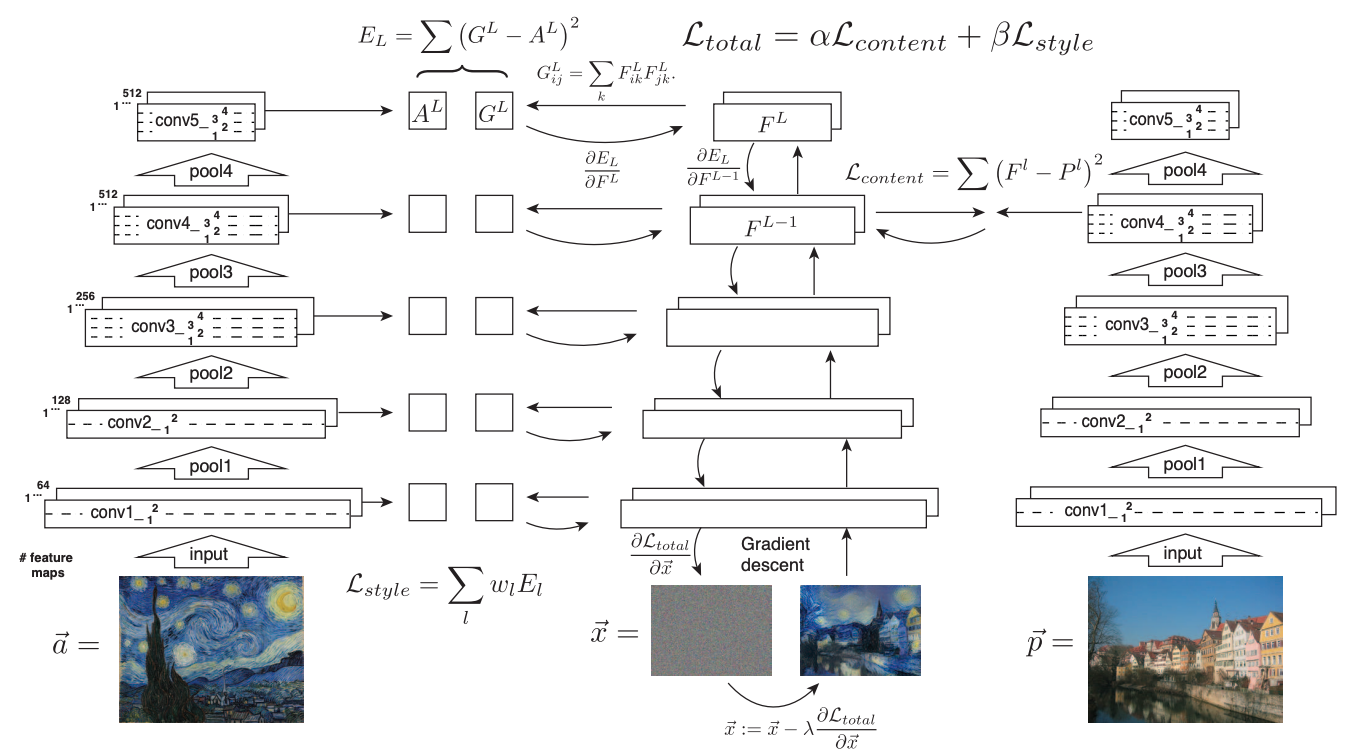
Result
论文给出了一些数据,模型使用VGG19,content来自conv4_2的输出;style则来自conv1_1,conv2_1,conv3_1,conv4_1,conv5_1几层的输出,${\alpha}/{\beta} = 1 \times 10^{-4}$,不同的$\alpha$和$\beta$的比值对结果影响如下

