Recurrent Neural Network
Sequence Data Notations
- $x^{\langle i \rangle}$, 表示输入$x$中的第$i$个token
- $y^{\langle i \rangle}$, 表示输出$y$中的第$i$个token
- $x^{(i)\langle t \rangle}$,表示第$i$条输入样本中的第$t$个token
- $y^{(i)\langle t \rangle}$,表示第$i$条输出样本中的第$t$个token
- $n_x$,表示某个输入token向量长度
- $n_y$,表示某个输出token长度
- $x_5^{(2)\langle 3 \rangle\langle 4 \rangle}$, 表示第二条输入样本中,第三个layer中第4个token向量中的第五个元素
以文本输入为例,假设我们有一个10000个单词的字典和一串文本,现在的问题是,找出下面文本中是人名的单词,输出结果是一维向量,其中1代表名字
x: "Harry Potter and Hermione Granger invented a new spell."
y: 1 1 0 1 1 0 0 0 0
我们用$x^{\langle i \rangle}$表示上述句子中的每个单词,则$x^{\langle 1 \rangle}$表示Harry, $x^{\langle 2 \rangle}$表示Potter,以此类推。假设在我们的字典中,and这个单词排在第5位,则$x^{\langle 1 \rangle}$的值为一个一维向量
注意上面的式子通常用列向量表示,即$x^{\langle i \rangle}$为[10000,1]。
在实际应用中,$x^{\langle 1 \rangle}$往往是一个2D tensor,因为我们通常一次输入$m$条训练样本(mini-batch)。我们假设
m=20,则此时我们有20列向量,我们可以横向将它们stack成一个二维矩阵。比如上面例子中,RNN在某个时刻的输入tensor的大小是[10000,20]的。
相应的,上述句子对应的$y$表示如下,其中$y^{\langle i \rangle}$表示是名字的概率
\[y = [1,1,0,1,1,0,0,0,0]\]Recurrent Neural Network
RNN的输入是一组sequence data,seguence中的每个$x^{\langle i \rangle}$会通过某一系列运算产生一个输出$y^{\langle i \rangle}$,并且该时间片上的输入除了有$x^{\langle i \rangle}$之外,还有可能来自前一个时间片的输出$a^{\langle i-1 \rangle}$,如下图所示
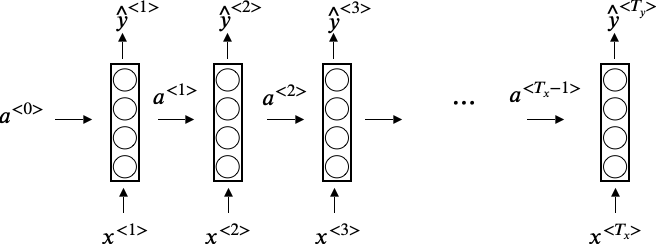
图中的$T$表示时间片,$a^{\langle {T_x} \rangle}$为$T$时刻的hidden state。我们令 $a^{\langle 0 \rangle} = 0$,则 $a^{\langle 1 \rangle}$ 和 $y^{\langle 1 \rangle}$的计算方式如下
\[a^{\langle 1 \rangle} = g(W_{aa}a^{\langle 0 \rangle} + W_{ax}x^{\langle 1 \rangle} + b_a) \\ \hat y^{\langle 1 \rangle} = g(W_{ya}a^{\langle 1 \rangle} + b_y)\]对于$a^{\langle t \rangle}$, 其中常用的activation函数为$tanh$或$ReLU$,对于$\hat y^{\langle i \rangle}$,可以用$sigmoid$函数。Generalize一下
\[a^{\langle t \rangle} = g(W_{aa}a^{\langle {t-1} \rangle} + W_{ax}x^{\langle t \rangle} + b_a) \\ \hat y^{\langle t \rangle} = g(W_y a^{\langle t \rangle} + b_y)\]简单起见,我们可以将$W_{aa}$和$W_{ax}$合并,假设,$W_{aa}$为[100,100], $W_{ax}$为[100,10000](通常来说$W_{ax}$较宽),则可以将$W_{ax}$放到$W_{aa}$的右边,即$[W_{aa}|W_{ax}]$,则合成后的矩阵$W_{a}$为[100,10100]。$W_a$矩阵合并后,我们也需要将$a^{ \langle {t-1} \rangle}$和$x^{\langle t \rangle}$合并,合并方法类似,从水平改为竖直 $[\frac{a^{\langle {t-1} \rangle}}{x^{\langle t \rangle}}]$得到[10100,100]的矩阵。
因此,我们需要学习的参数便集中在了$W_a$, $b_a$和$W_y$,$b_y$上。 在实际应用中,我们的$x$和$a$通常都是三维的矩阵
x.shape = (n_x, m, T_x)
a.shape = (n_a, m, T_a)
其中n_x表示x的one hot vector的长度(字典数量,比如5000),m表示batch size,即样本数量(句子个数),T_x则表示每个样本的时间片数量(可以理解为句子中token的个数)。而$x^{(i)}$或者$a^{(i)}$为某个时刻t`的切片,即
x_i = x[:,:,t]
a_i = a[:,:,t]
Numpy的实现如下
def rnn_cell_forward(xt, a_prev, parameters):
"""
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute next activation state using the formula given above
a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.dot(Wya, a_next) + by)
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
def rnn_forward(x, a0, parameters):
"""
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
a_next = a0
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a
a[:,:,t] = a_next
# Save the value of the prediction in y
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches"
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
Loss函数
上一节中我们已经看到,对每条训练样本来说,任何一个单词产生的输出$\hat y^{(i)\langle t \rangle}$是一个一维向量,形式和分类问题类似,因此对于单个单词的loss函数可以用逻辑回归的loss函数
\[L^{\langle t \rangle}(\hat y ^{\langle t \rangle}, y^{\langle t \rangle}) = - y^{\langle t \rangle}log{y^{\langle t \rangle}} - (1-y^{\langle t \rangle})log{(1-y^{\langle t \rangle})}\]则对于整个样本(句子),loss函数为每个单词loss的和
\[L(\hat y, y) = \sum_{t=1}^{T} L^{\langle t \rangle}(\hat y ^{\langle t \rangle}, y^{\langle t \rangle})\]反向求导的过程如下
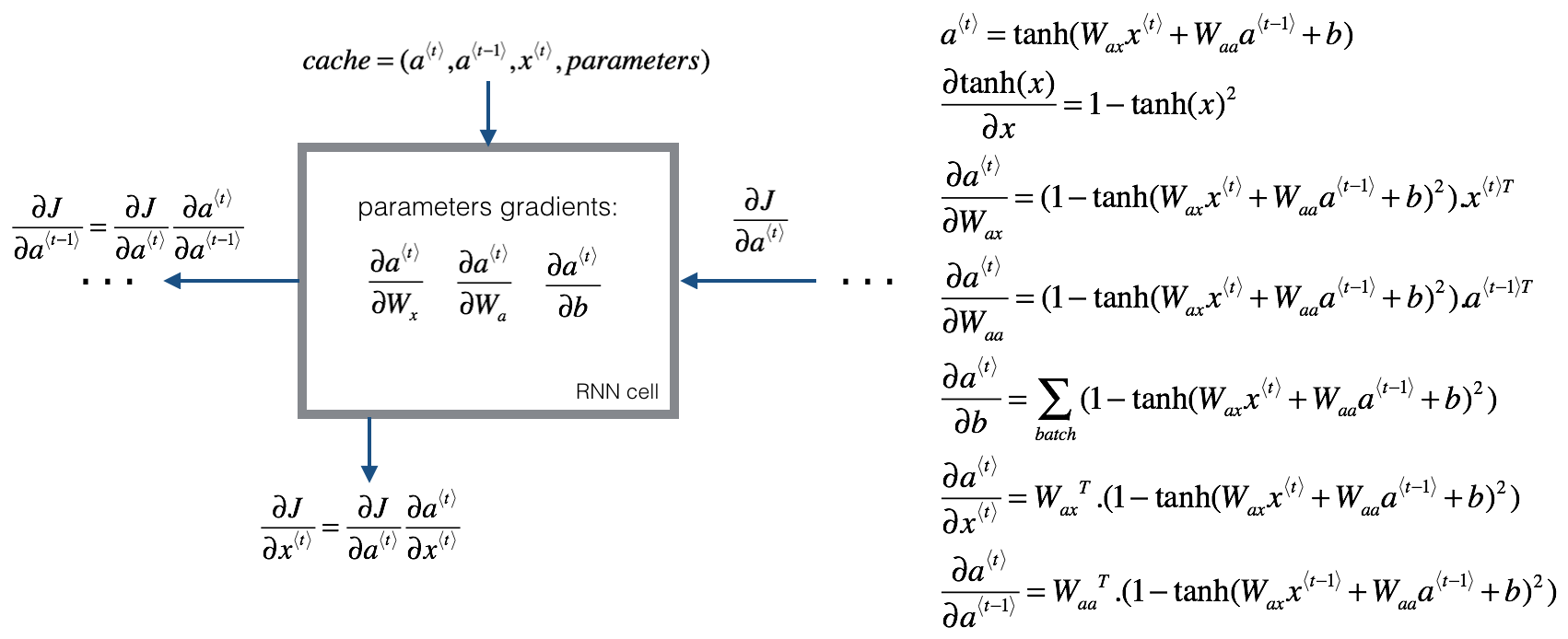
不同的RNN网络
除了上面提到的一种RNN网络外,根据实际应用的不同,RNN可以衍生出不同的结构,如下图所示
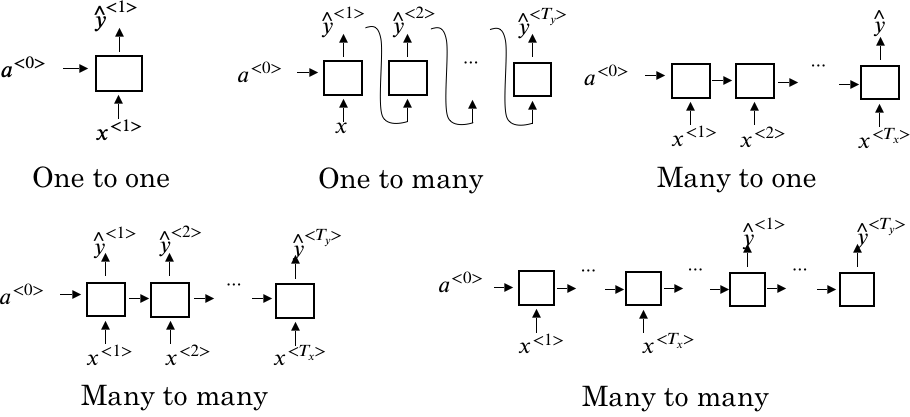
Language Model
Language Model有很多种,其输入为一个句子,输出为预测结果,通常以概率形式表示。假如我们的字典有10000个单词,输入文本如下
Cats average 15 hours of sleep a day. <EOS>
我们可以参考前面提到的RNN网络来构建我们的Model,如下图所示
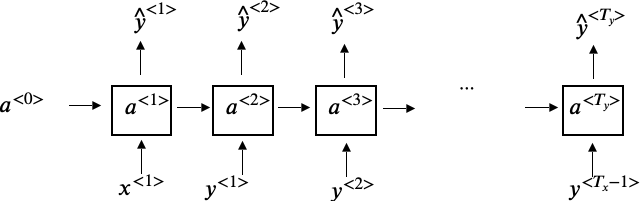
其中每个cell的结构如下图所示
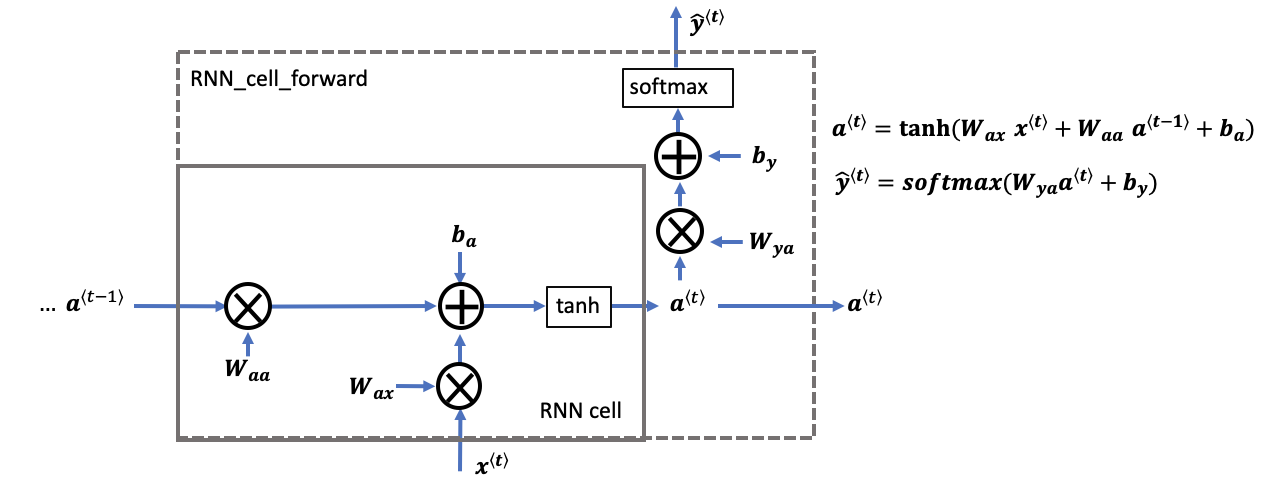
- 另$x^{\langle 1 \rangle}$和$a^{\langle 0 \rangle}$均为0,输出$\hat y^{\langle 1 \rangle}$是一个softmax结果,表示字典中每个单词出现的概率,是一个
[10000,1]的向量,由于未经训练,每个单词出现的概率均为1/10000 - 接下来我们用真实$y^{\langle 1 \rangle}$(”Cats”在字典中出现的概率)和 $a^{\langle 1 \rangle}$作为下一层的输入,得到$\hat y^{\langle 2 \rangle}$,其含义为当给定前一个单词为”Cats”时,当前单词是字典中各个单词的概率即 $P(?? |Cats)$,因此$\hat y^{\langle 2 \rangle}$也是
[10000,1]的。注意到,此时的$x^{\langle 2 \rangle} = y^{\langle 1 \rangle}$ - 类似的,第三层的输入为真实结果$y^{\langle 2 \rangle}$,即$P(average |Cats)$,和$a^{\langle 2 \rangle}$,输出为$\hat y^{\langle 2 \rangle}$,表示$P(?? |Cats average)$。同理,此时$x^{\langle 3 \rangle} = y^{\langle 2 \rangle}$
- 重复上述步骤,直到走到EOS的位置
上述的RNN模型可以做到根据前面已有的单词来预测下一个单词是什么
梯度消失
不难发现,上面的RNN模型是基于前面的单词来预测后面出现的单词出现的概率,但是对于一些长句子,单词前后的联系可能被分隔开,比如英语中的定语从句
The cat, which already ate ... , was full
The cats, which already ate ..., were full
上面例子例子中cat和was, cats和were中间隔了一个很长的定语修饰,这就会导致当RNN在预测was或者were时,由于前面的主语信息(cat或者cats)位置很靠前,使得预测概率受到影响(如果RNN能识别出此时主语是cat/cats则was/were的预测概略应该会提高)。具体在RNN中的表现是当做back prop时,由于网络太深,会出现梯度消失的问题,也就是说我们无法通过back prop来影响到cat后者cats的weight。
GRU
GRU(Gated Recurrent Uinit)被设计用来解决上述问题,其核心思想是为每个token引入一个GRU unit - $c^{\langle t \rangle}$,计算方式如下
\[\hat c^{\langle t \rangle} = tanh (W_c[c^{\langle {t-1} \rangle}, x^{\langle t \rangle}] + b_c) \\ \Gamma_u ^{\langle t \rangle} = \delta (W_u[c^{\langle {t-1} \rangle}, x^{\langle t \rangle}] + b_u) \\ c^{\langle t \rangle} = \Gamma_u ^{\langle t \rangle} * \hat c^{\langle t \rangle} + (1-\Gamma_u ^{\langle t \rangle}) * c^{\langle {t-1} \rangle}\]其中,$\Gamma_u ^{\langle t \rangle}$用来控制是否更新$c^{\langle t \rangle}$的值,$\delta$通常为sigmoid函数,因此$\Gamma_u ^{\langle t \rangle}$的取值为0或1;*为element-wise的乘法运算
回到上面的例子,假设我们cats对应的$c^{\langle t \rangle}$值为0或1, 1表示主语是单数,0表示主语是复数。则直到计算was/were之前,$c^{\langle t \rangle}$的值会一直被保留,作为计算时的参考,保留的方式则是通过控制$\Gamma_u ^{\langle t \rangle}$来完成
Tha cat, which already ate ..., was full.
c[t]=1 c[t]=1
g[t]=1 g[t]=0 g[t]=0 g[t]=0 ... g[t]=0
可以看到当$\Gamma_u ^{\langle t \rangle} $为1时,$c^{\langle t \rangle} = c^{\langle {t-1} \rangle} = a^{\langle {t-1} \rangle}$,则前面的信息可以被一直保留下来。
注意到$c^{\langle t \rangle}, \hat c^{\langle t \rangle}, \Gamma_u ^{\langle t \rangle}$均为向量,其中$\Gamma_u ^{\langle t \rangle}$向量中的值为0或1,则上面最后一个式子的乘法计算为element-wise的,这样$\Gamma_u ^{\langle t \rangle}$就可以起到gate的作用。
LSTM
Long Short Term Memory(LSTM)是另一种通过建立前后token链接来解决梯度消失问题的方法,相比GRU更为流行一些。和GRU不同的是
- LSTM使用$a^{\langle {t-1} \rangle}$来计算 $\hat c^{\langle t \rangle}$和$\Gamma_u ^{\langle t \rangle}$
- LSTM使用两个gate来控制$c^{\langle t \rangle}$,一个前面提到的$\Gamma_u ^{\langle t \rangle}$,另一个是forget gate - $\Gamma_f ^{\langle t \rangle}$
- LSTM使用了一个output gate来控制$a^{\langle t \rangle}$
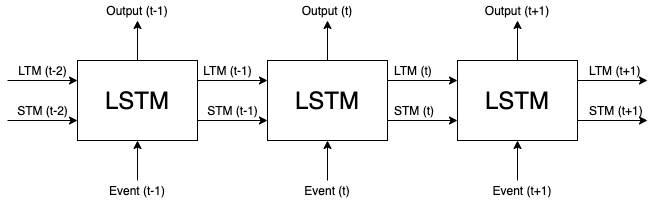
上述LSTM式子引入了三个gate函数,虽然步骤比较复杂,但是逻辑上还是比较清晰,也容易更好的整合到RNN网络中,下图是一个引入了LSTM的RNN的计算单元
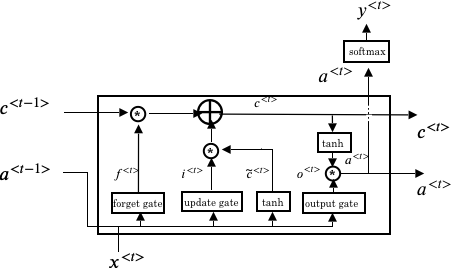
每个LSTM单元都是可微分的,它里面一共包含四种运算:加法,乘法,tanh和 sigmoid每种运算均可微。如果把各个LSTM单元串联起来,则RNN的模型变为
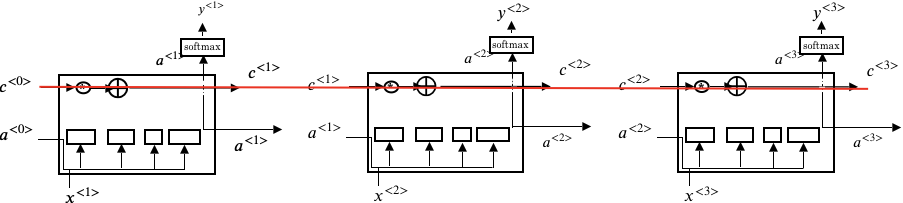
上述红线表示了$c^{\langle t \rangle}$的记忆过程,通过gate的控制,可以使$c^{\langle 3 \rangle} = c^{\langle 1 \rangle}$, 从而达到缓存前面信息的作用,进而可以解决梯度消失的问题。
另一种更加直观理解LSTM的方式是LSTM cell看成四个gate的组合
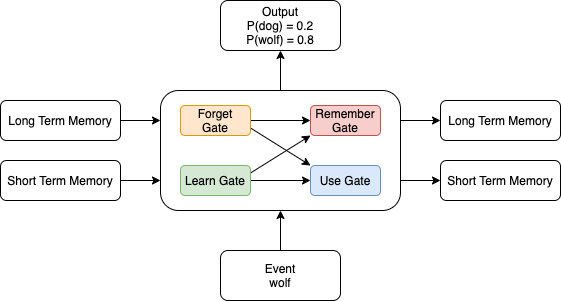
将每个RNN cell串联起来可已得到
Learn Gate
Learn Gate首先将short-term memroy($STM_{(t-1)}$)和$E_t$进行combine,然后将结果和一个ignore vector进行element-wise的相乘来决定矩阵中那些元素需要保留,哪些舍弃。这个ignore vector同样是通过$STM_{(t-1)}$和$E_t$生成,只是非线性函数用了sigmoid来限制输出的值域。
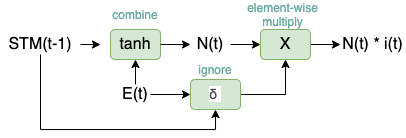
其中$N_t$和$i_t$表示为
\[N_t = tanh(W_n{[STM_{t-1}, E_t]}+b_n) \\ i_t = \delta(W_i{[STM_{t-1}, E_t]}+b_i)\]Forget Gate
Forget Gate用来控制long-term memory中哪些保留哪些舍弃,具体做法是$LTM_{t-1}$乘以一个forget factor$f(t)$。
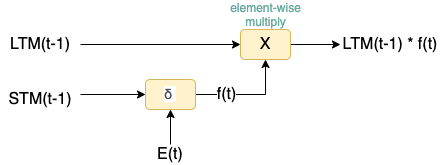
其中$f(t)$计算如下
\[f(t) = \delta(W_f{[STM_{t-1}, E_t]}+b_f)\]Remember Gate
Remember Gate将上面两个gate的输出进行相加
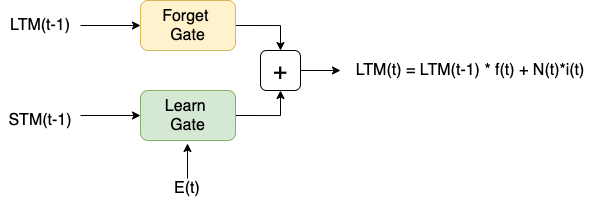
Use Gate
Use Gate的输入来自Learn Gate和Forget Gate,组合方式如下
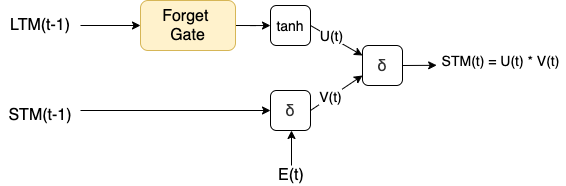
其中$U_t$和$V_t$的计算方式如下
\[U_t = tanh(W_uLTM_{t-1}f_t + b_u) \\ V_t = \delta(W_v[STM_{t-1}, E_t] + b_v)\]我们将上面四个gate组合到一起,可以得到下面的结果,和我们上面的结构类似
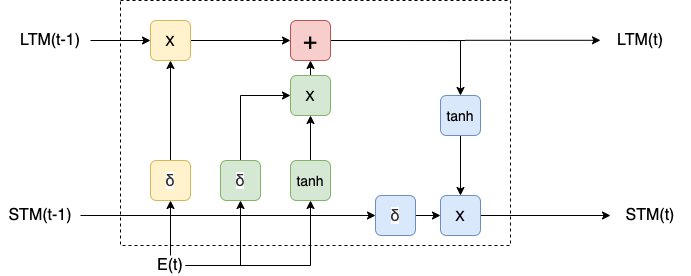
LSTM的numpy实现
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
c_next -- next memory state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
c stands for the cell state (memory)
"""
# Retrieve parameters from "parameters"
Wf = parameters["Wf"] # forget gate weight
bf = parameters["bf"]
Wi = parameters["Wi"] # update gate weight (notice the variable name)
bi = parameters["bi"] # (notice the variable name)
Wc = parameters["Wc"] # candidate value weight
bc = parameters["bc"]
Wo = parameters["Wo"] # output gate weight
bo = parameters["bo"]
Wy = parameters["Wy"] # prediction weight
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
concat = np.zeros((n_a + n_x, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft, it, cct, c_next, ot, a_next
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell
yt_pred = softmax(np.dot(Wy, a_next) + by)
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
def lstm_forward(x, a0, parameters):
"""
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
bi -- Bias of the update gate, numpy array of shape (n_a, 1)
Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
bo -- Bias of the output gate, numpy array of shape (n_a, 1)
Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
c -- The value of the cell state, numpy array of shape (n_a, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
"""
# Initialize "caches", which will track the list of all the caches
caches = []
### START CODE HERE ###
Wy = parameters['Wy'] # saving parameters['Wy'] in a local variable in case students use Wy instead of parameters['Wy']
# Retrieve dimensions from shapes of x and parameters['Wy']
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# initialize "a", "c" and "y" with zeros
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next
a_next = a0
c_next = np.zeros(a_next.shape)
# loop over all time-steps
for t in range(T_x):
# Get the 2D slice 'xt' from the 3D input 'x' at time step 't'
xt = x[:,:,t]
# Update next hidden state, next memory state, compute the prediction, get the cache
a_next, c_next, yt, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a
a[:,:,t] = a_next
# Save the value of the next cell state
c[:,:,t] = c_next
# Save the value of the prediction in y
y[:,:,t] = yt
# Append the cache into cache
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
