The Histogram Filter Approach for Robot Localization
Course Notes from Udacity Self-Driving Car Nanodegree Program
Prerequisite
概率分布模型
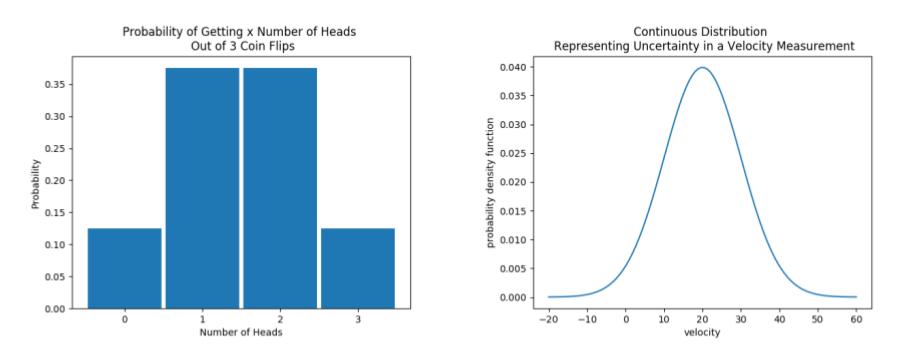
概率分布模型是概率的一种数学描述,和任何一种数学公式一样,概率模型可以被二维可视化,也可以用于线性代数和微积分的计算。概率统计模型有两种,一种是离散概率,一种是连续概率。其分布曲线如下图所示:
- 对于离散概率分布函数
g(x),有如下性质- 对于所有的
x值,对应的y值均大于等于0 - 对于任意
x值,其对应的y值表示该x事件发生的概率p(x) - 所有
g(x)值的和为1 - 对任意
g(x)的值均小于等于1
- 对于所有的
- 对于连续概率分布函数
f(x),有如下性质- 对于所有的
x值,对应的y值均大于等于0 - 对于任意
x值,它的概率为0 - 对于某个区间内的event发生的概率为该区间的面积
f(x)的面积为1- 对任意
f(x)的值可以大于1
- 对于所有的
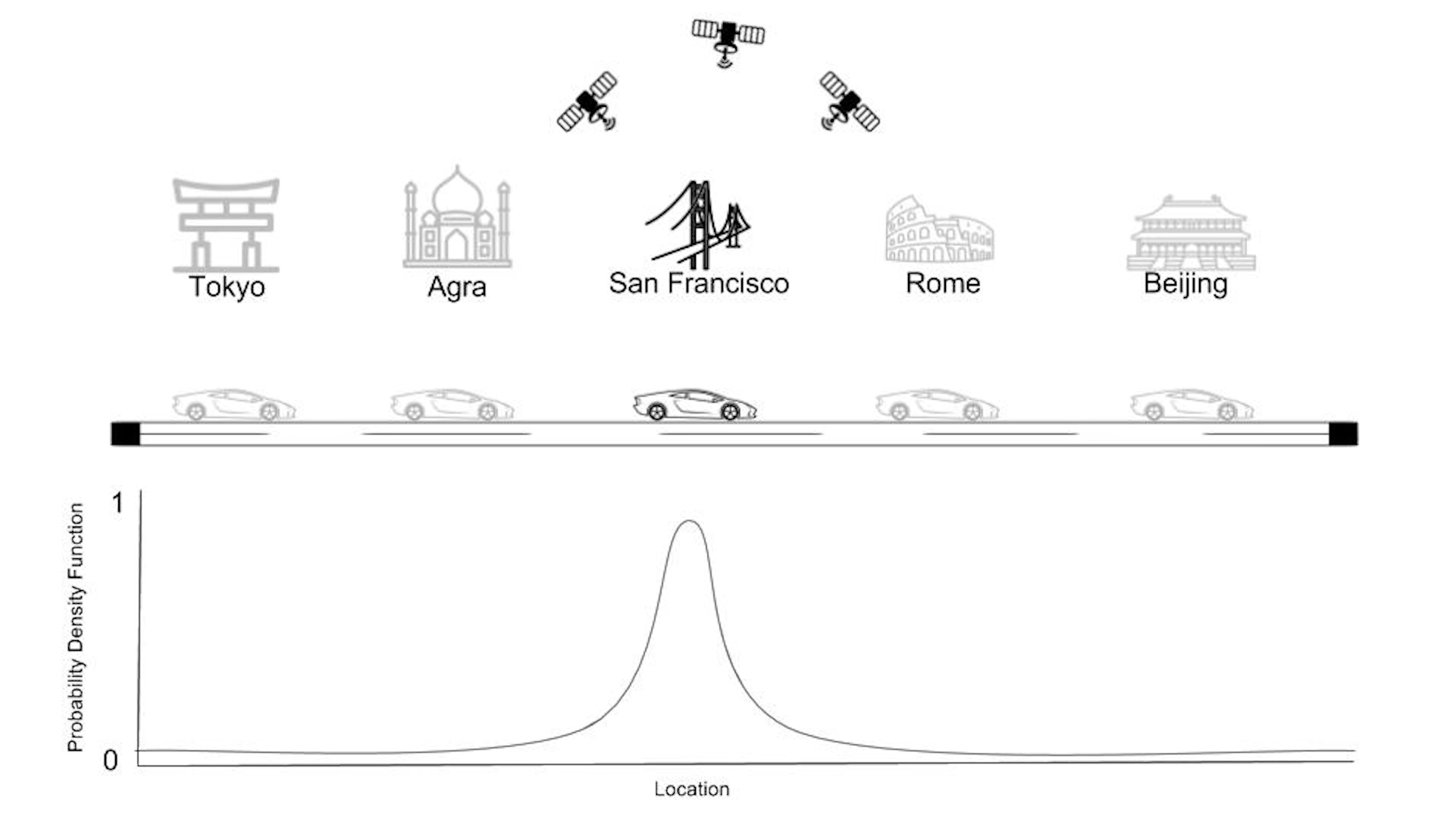
Localization的原理
在上一篇文章的末尾,我们曾简单的提到了机器人定位自己位置的大概原理,通常的做法是先使用多个GPS进行定位,然后再结合自身各种传感器采集的数据进行位置矫正。一种矫正的方法是使用到卡尔曼滤波,这一节我们先通过一个简单的一维离散模型初步认识一下卡尔曼滤波的过程。
Sense
假设我们有一个机器人,想要从A点走到B点,AB之间可以平均分成5个格子,则在没有任何信息输入的情况下,机器人认为自己位于AB之间某一位置的概率为1/5=0.2,这个概率称为先验概率。
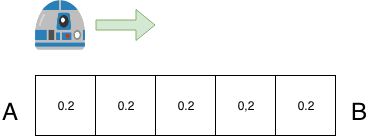
我们可以用一个Python数组表示每个位置的概率为:
p=[0.2,0.2,0.2,0.2,0.2]
而实际上我们的机器人是装有传感器的,他可以感知每个格子中的颜色。由前一篇文章可知,通过传感器,机器人可以引入额外的信息,根据贝叶斯公式,这些信息可以帮助我们矫正先验概率,从而得到更为准确的后验概率。
我们假设AB之间的5个格子为绿色或者红色中的某一种,机器人的传感器可以识别颜色,则引入传感器后,机器人可以更精确的描述自己在AB两点之间的位置。比如当传感器感知到红色的时候,机器人知道自己可能大概率处于红色的格子里,那么在机器人眼中红色格子的概率就应该大于0.2,相应的绿色格子的概率就应该小于0.2。
那么该如何量化这个概率呢?答案是使用贝叶斯公式,我们将红色,绿色格子中的先验概率0.2乘以各自的矫正因子,假设红色的矫正因子为0.6,绿色为0.2,则可以得出下面结果:
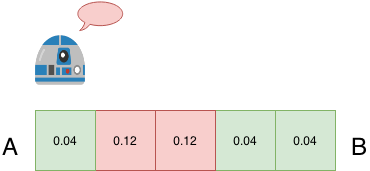
将上面结果归一化后得到下面结果:

这个结果表示的是当机器人的传感器感知到红色时,5个格子的概率分布。其概率含义如下:当机器人看到红颜色时,位于红色格子的概率为1/3,位于绿色格子的概率为1/9,即
上面从先验概率通过贝叶斯公式得到后验概率的过程称为Sense,我们可以接种用Python描述上述过程:
p=[0.2, 0.2, 0.2, 0.2, 0.2] #先验概率
world=['green', 'red', 'red', 'green', 'green'] #格子颜色
#调整因子
pHit = 0.6
pMiss = 0.2
#Z为传感器残疾结果
def sense(p, Z):
q=[]
for i in range(len(p)):
hit = (Z == world[i])
## 贝叶斯公式,求乘积
q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
#归一化
total = sum(q)
q = map(lambda x:x/total,q)
return q
sense函数非常重要,接下来会不断使用这个函数,因此一定要充分理解。回到上面的例子,当机器人sense到自己红色的时候,此时自己内部的概率分布发生了变化,从左图变成了右图
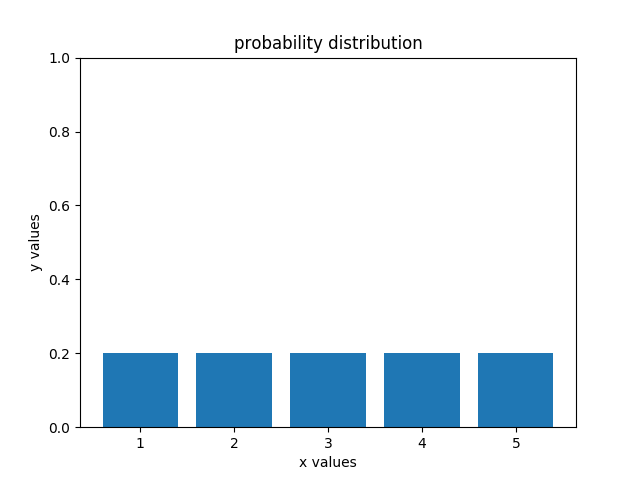
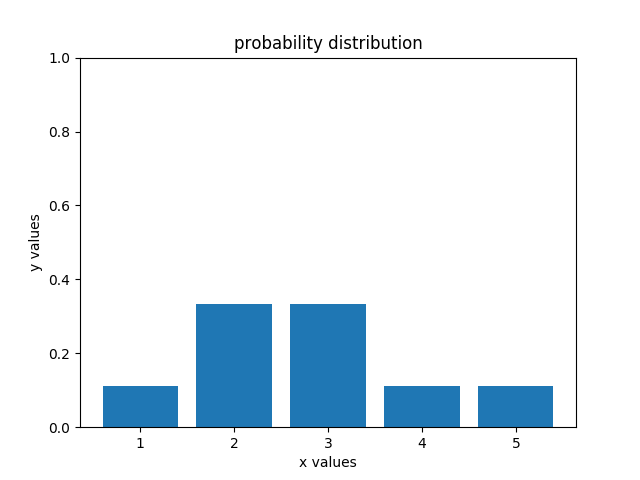
右图说明,机器人大概率知道自己位于第2号或者第3号格子内,但是具体在哪一个格子自己并不清楚,想要知道自己具体在哪个格子里需要再引入额外信息进行判断,于是机器人向前移动了一步,又进行了一次sense
p = move(p,1)
p = sense(p,'green')
对于move函数下一节会具体介绍,这里可理解为机器人向前移动了一个格子
此时,机器人发现自己移动了一格后,sense到了绿颜色,于是概率分布又发生了变化:

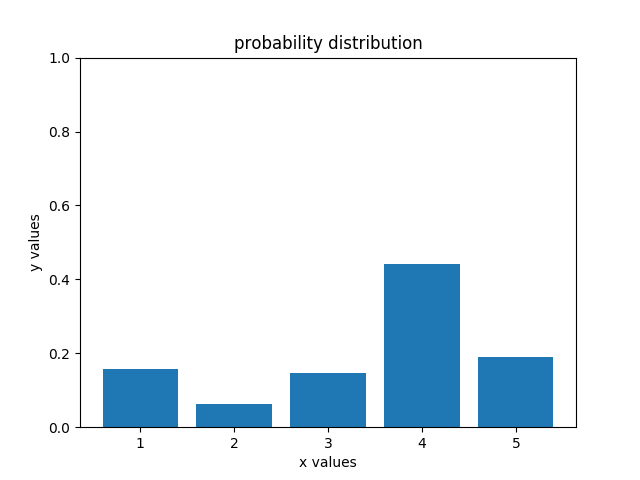
新的概率分布如右图所示,我们发现第4个格子的概率最大,此时机器人便可以明确的知道自己位于第4个格子中了。
当我们有了sense函数之后,机器人就可以边移动,边采集数据,然后不断更新每个位置上的概率从而确定自己的位置:
p = sense(p,'red')
p = move(p,1)
p = sense(p,'green')
p = move(p,1)
...
简单总结一下,机器人通过传感器不断引入观测数据,从而完成了将原先均匀分布的先验概率提升为包含一定位置信息的后验概率概率。sense的本质上是一种引入信息的过程,它会提高系统整体的熵。
Move
回到定位问题上,除了上面提到的sense问题以外,我们还需要考虑另一个问题,就是机器人的移动问题。所谓移动问题是指机器人在前进过程中并不能总是能准确的移动到某个位置。比如,我们想让一个机器人向右移动一格,而当机器人移动时,它有一定的概率出错,比如移动了两格或者没移动,因此移动的不准确同样也会造成概率分布的混乱。
我们举一个具体的例子,还是假设机器人从A移动到B,AB之间有5个格子,而此时,机器人已经明确知道自己在第2个格子中,即概率分布为:
p = [0,1,0,0,0]
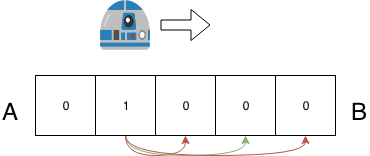
假设机器人现在想要向右移动2个格子,但由于会有一定几率的出错,根据多次试验的结果,假设我们统计出了下面数据:
上面数据的含义是,假设机器人位于i的位置,那么它移动到i+2的位置的概率为0.8,移动1格或3个的概率为0.1。此时当机器人前进2格时,对应的概率分布变成了:
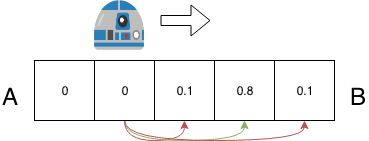
p = [0,0,0.1,0.8,0.1]
可见机器人的每次移动实际上都是丢失信息的,体现在从一个确定的位置(概率为1)变为三个不确定的位置(概率分别为0.1,0.8,0.1)。可以想象一下,假如机器人不停的移动1000次(假设走到第5个格子之后又回到第1个格子),概率分布会变成怎样呢?我们可以来一起计算一下
def move(p, U):
q = []
for i in range(len(p)):
s = pExact * p[(i-U) % len(p)]
##计算全概率,求和
s = s + pOvershoot * p[(i-U-1) % len(p)]
s = s + pUndershoot * p[(i-U+1) % len(p)]
q.append(s)
return q
p=[1,0,0,0,0]
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1
for _ in range(1,10001):
p = move(p,1)
print(p) #[0.2,0.2,0.2,0.2,0.2]
如果不理解move函数可以不必关注其细节,只需观察move前后的概率分布变化即可
上面结果可以看出,如果移动的次数足够多,概率分布将变为均匀分布,变化如下图所示
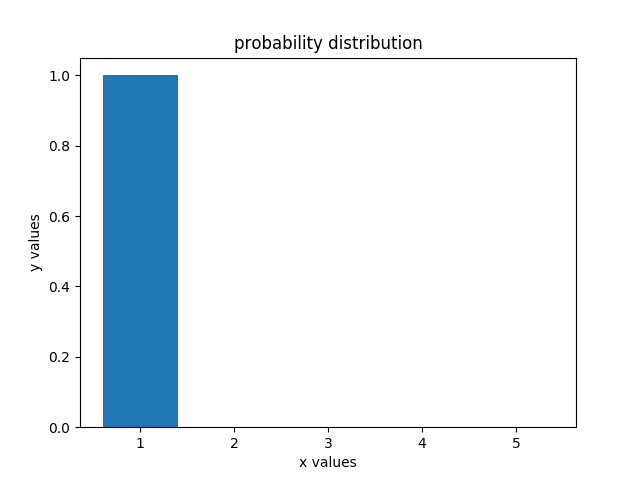
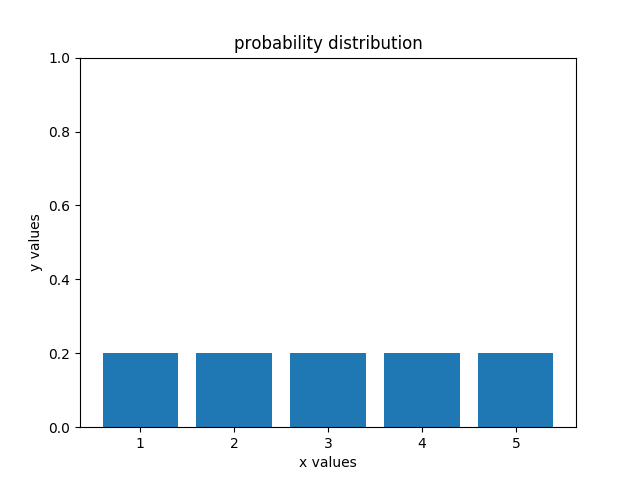
总结一下,对于move来说,本质上是一个损失信息的过程,每次机器人移动都会引入一定的不确定性,移动的次数越多,每个位置的不确定性会越大,系统整体的熵会降低最终达到均匀分布的状态。
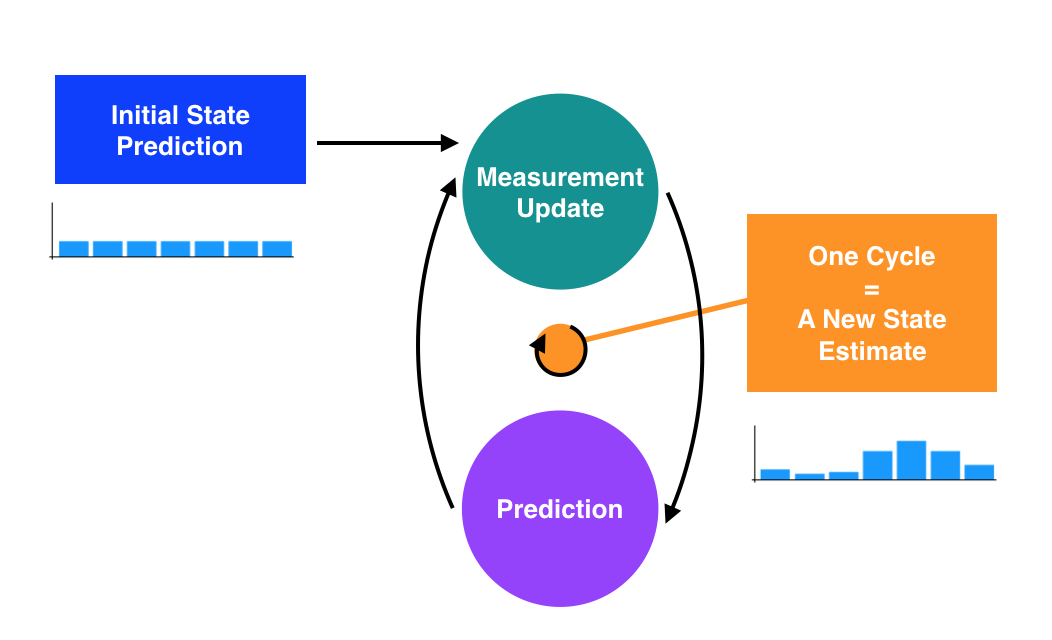
Sense and Move
了解了sense和move,我们不难发现,机器人移动的过程实际上就是不断获得新信息和不断损失信息的交替循环,机器人没移动一步,会通过传感器得到一个观测值来矫正自己的位置,同时又因为移动带来的不确定性而损失掉一部分信息。这个过程可以如下图所示:
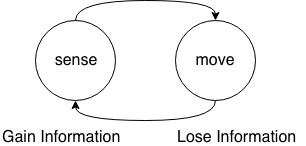
我们可以接着用代码来模拟下这个过程
p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
motions = [1,1]
for k in range(len(measurements)):
#sense
p = sense(p,measurements[k])
#move
p = move(p,motions[k])
上述代码中,机器人先sense到了red,然后向右移动1个格子,接着又sense到了green,然后向右又移动了1个格子,此时得到的概率分布如左图所示
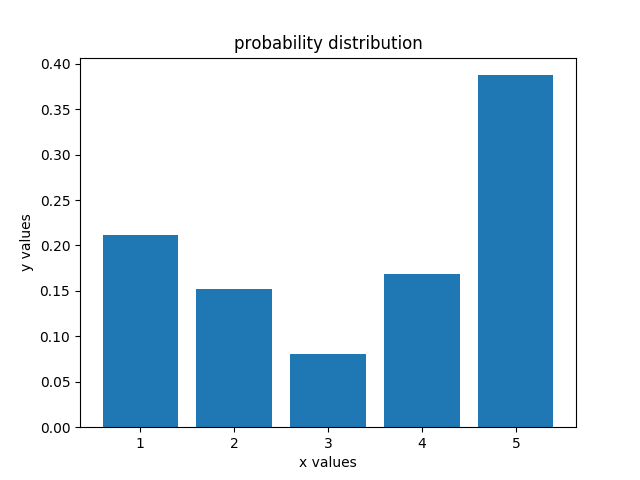
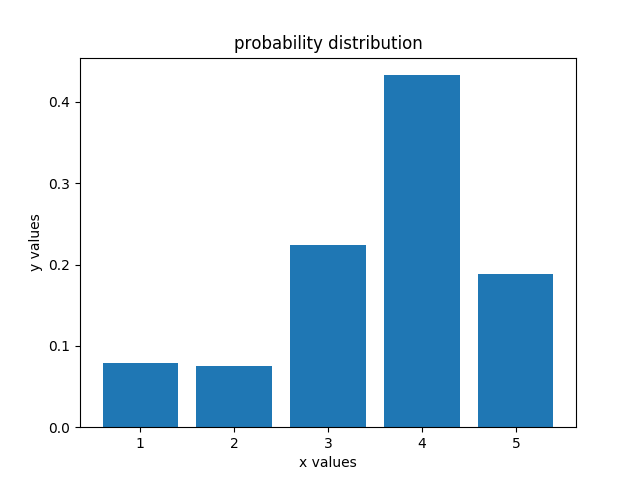
观察左图可发现,第5个格子的概率最大,说明机器人知道自己目前在第5个格子中。假如我们将measurements改为['red','red'],概率分布变为右图,此时机器人知道自己位于第4个格子里,这也符合我们的推测。
小结
这一节我们给出了一种确定机器人位置的理论模型和实现方法。我们先来一起回顾下这个过程,首先我们需要有一个位置的先验概率,然后通过sense函数来提升先验概率,从概率角度看,sense的过程是使用贝叶斯定理求乘积的过程。接下来由于机器人在移动过程中会带来不确定性,因此会损失一部分信息,从概率分布上看,损失信息的过程是求全概率的过程(求和)。最后机器人通过不断的sense和move来更新概率分布。整个过程如下图所示