The Kalman Filter Approach for Robot Localization

Posted on 2018-08-12 | Post modified 2018-08-30 | In AI , Autonomous-Driving

一维卡尔曼滤波

如果理解了前面使用直方图进行Localization的原理，也就大概理解了卡尔曼滤波的原理。这一节我们会继续对上一一篇文章中的例子再进行一些完善，将离散概率分布函数变成连续的概率分布，因为在现实世界中，位置往往是时间的函数，而时间是连续的，因此我们需要用一个连续概率函数对上述场景进行模拟。

不论概率分布式是离散还是连续的，其定位的原理是不变的，都是sense和move两个过程的交替更迭。

高斯函数

回顾前面介绍Localization的步骤，第一步是需要有一个先验概率，一个连续型的概率密度函数，这个函数可以使用高斯函数来表示，

$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} exp ^{-\frac{(x-\mu)^2}{\sigma^2}}$

对于高斯函数来说，方差越大，概率分布函数越“胖”，样本偏离均值的幅度越大；相反的，方差越小，样本偏离均值的幅度越小，概率分布函数越“瘦”。如果用高斯函数来描述机器人的位置，我们希望方差越小越好，这样均值位置就越接近机器人的真实位置。

更多关于高斯函数的特性请自行查阅文档。

Measurement Update

回到定位问题上，假设我们有一个先验的高斯概率密度函数为$f(x)$，其均值和方差分别为(mu=120, sigma=40)，校验因子的概率密度函数为$g(x)$，其均值和方差分别为(mu=200,sigma=30)，如下图所示

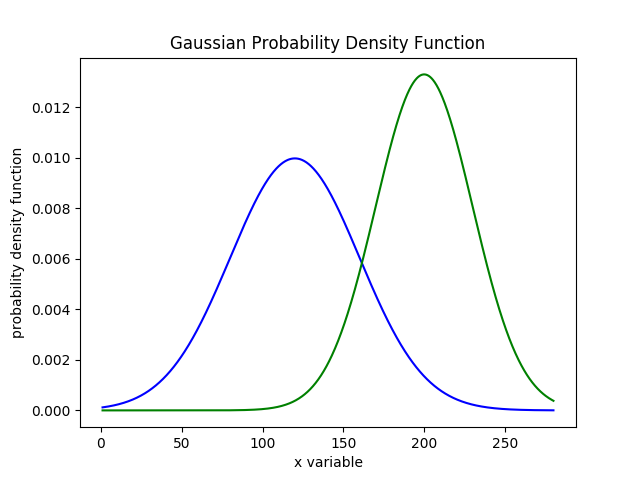
接下来机器人进行了一个次measure，根据贝叶斯公式，后验概率应该等于$f(x)*g(x)$，得到的结果如下图

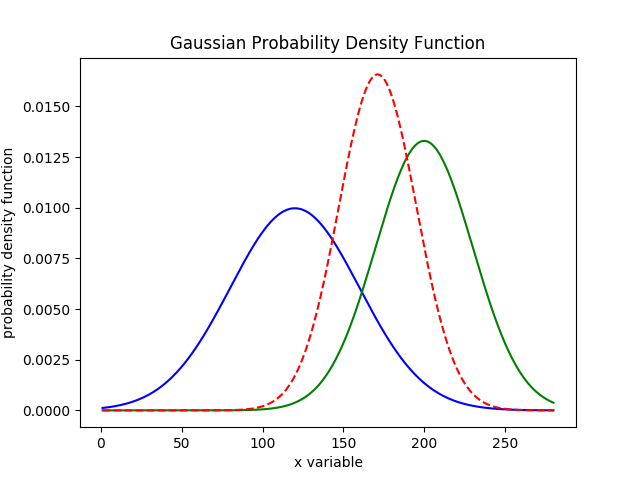
从这个结果中，我们能观察出几条重要的结论：

计算后的高斯分布的均值位于120和200之间
方差变的更小，峰值为三者最高，说明measure获取了新的信息，提高了位置预测准确率

产生这个结果的原因从直观上不太好理解，实际上可以从数学的角度进行证明，当两个高斯函数相乘后，产生的新的均值为

$\mu = \frac{\sigma^{-2}_1\mu_1 + \sigma^{-2}_2\mu_2}{\sigma^{-2}_1 + \sigma^{-2}_2}$

由于$\mu_2 > \mu_1$，很直观的有 $\mu_1<\mu<\mu_2$。相应的，产生的新的方差为

$\sigma^2 = \frac{\sigma^2_1\sigma^2_2}{\sigma^2_1+\sigma^2_2}$

这个看起来没有那么直观，我们不妨代入几个数试试，令$\sigma^2_1 = \sigma^2_2 = 4$，$\sigma=2$的值为2；令$\sigma^2_1 = 8$,$\sigma^2_2 = 2$，$\sigma=1.6$，以此类推。

measure过程的Python代码如下：

def measure(mean1, var1, mean2, var2):
    new_mean = (var2 * mean1 + var1 * mean2) / (var1 + var2)
    new_var = 1/(1/var1 + 1/var2)
    return (new_mean, new_var)

为了简化计算，上述代码只返回了均值和方差，如果要计算对于高斯函数，将其带入即可

Motion Update

sense完之后就可以开始move了，move是一个损失信息的过程，为了量化损失的信息，我们引入一个损失概率密度函数，该函数也服从高斯分布，我们用(u,r)表示，其中u是均值，r是方差。为了计算损耗后的概率分布，我们只需要让当前的概率密度函数和损失概率密度函数“求和”即可：

$\mu' = \mu + u \\ \sigma'^2 = \sigma^2 + r^2\\$

因此我们可以写出move的代码:

def predict(mean1, var1, mean2, var2):
    new_mean = mean1 + mean2
    new_var = var1 + var2
    return (new_mean, new_var) 

sense & move

将生面的sense和move结合起来，我们就得到了一维卡尔曼滤波的完整过程:

import math
from Kalman.predict import predict
from Kalman.measure import measure

##先验概率
mu = 0
sig = 1000

##矫正因子
measurements = [5.0,6.0,7.0,9.0,10.0]
measurement_sig = 4.0

##损耗因子
motion = [1.0,1.0,2.0,1.0,1.0]
motion_sig = 2.0

## sense and move
for index in range(0,len(measurements)):
    #sense
    (mu,sig) = measure(mu,sig, measurements[index],measurement_sig)
    #move
    (mu,sig) = predict(mu,sig, motion[index],motion_sig)

上述代码逻辑和前面离散demo基本一致，不同的是概率密度函数变成了连续的高斯函数，这里就不再做过多的分析。下图为移动5次后的概率分布结果