首页 | Home
博客 | Blog
关于 | About

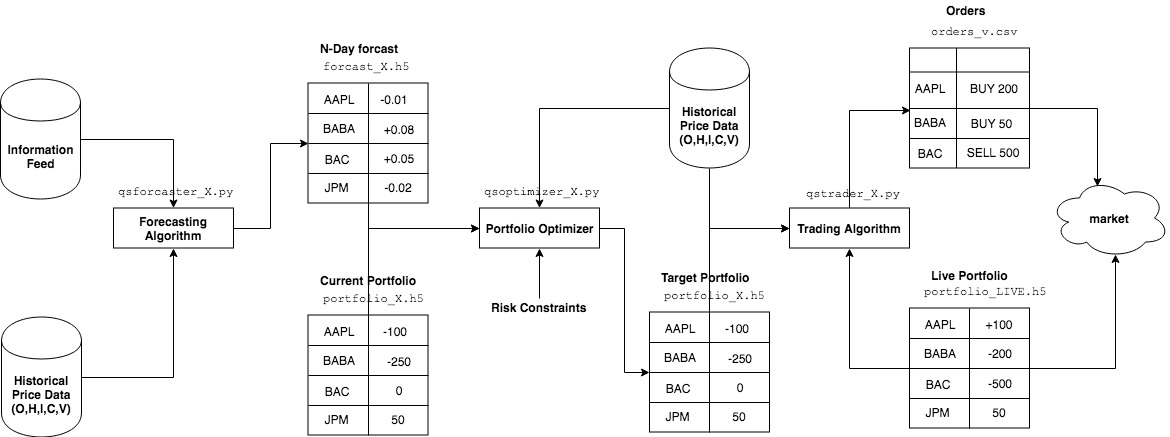
资产组合与市场机制

Posted on

Online course from Coursera & Udacity

Portfolio Management

  • Expense ratio
    • Used by mutual funds & ETFs
    • Usually less than 1%
  • “Two and twenty”
    • Classic structure for hedge funds.
    • 2% of assets under management + 20% of the returns.
    • 1M with 20% per year = 60k per year
  • How/Why different?
    • 共同基金或者ETF基金经理目标是增大基金数额来赚取管理费
    • 私募基金或者对冲基金经理目标是提高基金收益

How to Attract Investors

  • 资金来源
    • Individuals
      • 个人投资者，资金占比较少
    • Institusions
      • 机构投资者
        • Harvard Foundation
        • CalPERS
    • Funds of Funds
      • 来自其他基金的投资
  • Two Main Types of Fund Goals
    • Reference to a benchmark
      • 有指标参考，比如跑赢S&P500等
    • Absolute return
      • 低风险策略，只关注收益回报

Metrics for Assessing Fund Performance

  • Common Metrics
    • Annual Return
      • metric:
        • (value[end] / value[star])) -1
        • (value[end] - value[start])/value[start]
      • Example: $100 to $110
        • (110/100) -1 = 0.1 = 10%
        • (110-100)/100 = 0.1 = 10%
    • Risk
      • 定义风险：Standard deviation of return
        • daily return
          //日回报保准差
  daily_rets[i] = (value[i]/value[i-1]) -1
  std_metrics = stdev(daily_rets)
      • Draw down
        • 最大跌幅
        • 平均跌幅
  • Reward/Risk
    • 收益风险比，How much reward you are getting for your risk?
    • Sharpe Ratio
      • Most “important” measure of asset performance.
      • How well does the return of an asset compensate the investor for the risk taken
      • The higher the Sharpe ratio the better.
      • When comparing two assets each with the same return, higher ratio gives more return for the same risk.
      S = E [ R-Rf ] σ = E [ R-Rf ] var E [ R-Rf ] = K* dailyRet std(dailyret)

      • seudo code

          metric = k * mean(daily_rets)/stdev(daily_rets)
  # k = sqrt(250) for daily returns
  # 250: days in a trading year
    • Sortino Ratio
      • Sortino ratio only penalizes for negative volatility in the calculation of risk.
      • Sharpe ratio penalizes for both positive and negative volatility.
    • Jensen’s Alpha
  • Example

假设有一只Fund，它参考Dow Jones指数的benchmark如下：

  Return Sharpe STDEV D-down Corr
xxFund 33% .94 0.58% -8.67% 0.89
$DJI 43% .63 1.23% -27.38% 1.00
  1. 该基金没有收益率没有跑赢大盘，但是Sharpe指数高于大盘，说明它的整体波动率较低，相对于收益的风险更小
  2. 同样，STDEV，D-down 数据也偏低，说明日均波动较小

Market Mechanics

  • Types of Orders
    • But,Sell
    • Market, Limit
    • Shares
    • Price(if Limit)
    • Additional possibilities:
      • Sell short
    • More complex orders
  • The Order Book(买盘与卖盘)
    • Ask (Buy)
    • Bid (Sell)
  • Mechanics of Short Selling
    1. Borrow the shares 像券商融券
    2. 立刻卖掉融到的券
      • 拿到现金
      • 需要在未来归还券商融到的股票
    3. 如果价格未来价格下跌
      • 只需要支付较低价格来买回股票还给券商
      • 差价即是利润

Computing Inside a Hedge Fund

Company Worth

假设我们今天有

  • 使用折现率

假设我们投资一家公司，这个公司每年一股能产生1美金的利润(dividend)，那么我们现在应该以每股多少钱购入它的股票？换句话说，这个公司现在每股的价值该怎么计算，或者说这个公司的固执该怎么计算呢？为了比较，假设我们也可以把买这家公司股票的前钱存到银行，同样每年能赚取1美金。假设银行的利息是1分钱，那么我们需要向银行存入0.99美元，一年后能拿到1块钱。对于公司来说，它承担的风险比银行高，因此它的收益也比银行高，假设我们只需要投资0.95美元一年后即可得到1块钱收益。这意味着

一年后1美元利润，现在只值0.95美元。而0.95/1这个比例值也叫做这个折现率（discount rate）

|now          |year1      |year2     |year3
Company ----> $1.00 ----> $1.00 ---->$1.00 --->...
$0.95
Bank   -----> $1.00 ----> $1.00 ---->$1.00 --->...
$0.99

注意，上面提到的折现率不仅仅是针对的一年的，而是无限长时间内的，而时间越长，1美元折现的价值越低, 如果过了几百年，1美元折现到现在基本上约等于0。这也意味着一家每年固定利润为1美金的公司，随着时间的增长，它的估值并不是无穷大的，因为未来的1美金对于现在来说，基本上就等于0

--->0.95---->0.95^2----->0.95^3......-->~0.0
    |year1  |year2      |year3       |year n

我们可以通过折现率用下面公式计算一家公司的估值

\[Value=Sum(dividen*gamma^i) = \sum_{i=1}^\infty dividen * gamma^i = {dividend * 1}/{(1-gamma)}\]

其中$dividen$表示公司的每股利润（股息），$gamma$表示折现率，上面例子中，这家公司的估值为20美金

\[Value=\sum_{i=1}^\infty 1.00 * 0.95^i=\frac{1.00}{(1-0.95)}=20.00\]
  • Book Value
    • 净资产
    • “Total” assets minus intangible assets and liabilities.

综上所述，公司的价值为：未来估值+净资产。另一种更直观的计算方式为：#(outstanding shares) * price 即流通股数 * 股票价格

CAPM

CAPM是Capital Assets Pricing Model的缩写，翻译过来叫做资本资产定价模型。1966年由Jack Treynor, William Sharpe, John Linter和Jan Mossin共同提出，其中Sharpe,Markowitz和Merton Miller还因此共同获得了诺奖。这个理论的提出，改变了当时人们对投资的理念，基于这个模型和有效市场假说，有观点认为投资指数基金或者配置资产来跟踪指数是比较好的选择，也就是所谓的被动投资。

本课程的投资观点（量化交易）是一种主动投资的理念，Tucker Balch指出基于这种理念也可以取得不错的汇报，但是CAPM模型影响力非常大，是各种投资产管理理论的基础，因此有必要仔细了解

  • CAPM假说
    • Return of stock has two components:
      • Systematic (the market)
      • Residual
    • Expected Value of residual = 0
    • Market return
      • Risk free rate of return + Excess return

上图为BABA和NASDAQ近三个月的走势叠加图, 可以看到大部分时间BABA和NASDQ的走势基本持平。波动的部分则为BABA自身的股价变化。CAPM认为股价由两方面决定， 一方面市场波动，一方面是个股波动。他们之间的关系为

\[\gamma_i=\beta_i * \gamma_m + \alpha_i\]

$\gamma_i$表示股价，它的值为市场波动系数$\beta_i$乘以前一天的价格加上个股当天波动的价格$\alpha_i$。按照CAPM理论，在大部分时间内，某家公司的股价应该随着指数的波动而波动，即$\alpha_i$的期望为0，而如果表现出偏离，则说明这家公司具备某些可以挖掘的信息。

Resources

附 Install QSTK on MacOS

官方指南 有些步骤已经过时，这里整理一份暂时可用的，测试通过了\Examples\Basics\下的所有tutorial.py，环境为Python2.7

  • Install Pip
brew install python
pip install --upgrade setuptools
pip install --upgrade pip
  • Install virtualenv
pip install nose
pip install virtualenv
  • Install Numpy, Scipy and Matplotlib

这些库依赖gfortran，后者在brew库中已经被移到gcc，因此这里brew install gfortran会失败，可以用gcc替代:

brew install gcc

如果在执行make时卡住，尝试更新XCode插件sudo xcode-select --install。 安装GCC成功后，还需要先更新home brew的两个Science库:

brew tap brewsci/homebrew-science
brew tap brewsci/bio

然后安装 Numpy, Scipy and Matplotlib

brew install numpy
brew install scipy
brew install matplotlib
  • 创建一个QSTK的测试目录
mkdir ~/QSTK
cd ~/QSTK
  • 使用virtualenv进行环境隔离
virtualenv env --distribute --system-site-packages
source ~/QSTK/env/bin/activate

activate之后的安装都将与全局环境隔离，这里要先check一下env/lib/下的python版本， 如果误使用了python3，要还原回来，需要重新指定python版本

virtualenv --python=/usr/bin/python2.7 ~/QSTK/env
  • 安装QSTK及其依赖
pip install pandas
pip install scikits.statsmodels
pip install scikit-learn
pip install cvxopt
pip install QSTK

创建matplotlib配置文件:echo "backend: TkAgg" > ~/.matplotlib/matplotlibrc

  • 测试QSTK demo
curl -O https://spark-public.s3.amazonaws.com/compinvesting1/QSTK-Setups/Examples.zip
unzip Examples.zip

使用Examples目录中的Validation.py进行测试，如果发现TimeSeries类找不到：

2.7.14_3/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/QSTK/qstkutil/qsdateutil.py", line 36, in _cache_dates
    return pd.TimeSeries(index=dates, data=dates)
AttributeError: 'module' object has no attribute 'TimeSeries'

原因是panda版本过新，还原到0.7.3版本

pip install pandas==0.7.3
  • 测试Basic下的一系列tutorial.py
python tutorial1.py

如果发现

numpy TypeError: The numpy boolean negative, the `-` operator, is not supported, use the `~` operator or the logical_not function instead.

则表示numpy的版本不对，具体是哪个版本还不清楚，暂时的解法是按照提示去出错的地方，修改代码。上述步骤完成后，测试tutorial1.py，成功后可发现Basics目录下生成了多个pdf文件

  • 退出virtutalen环境
/bin/deactive
  • 卸载QSTK
rm -rf ~/QSTK