PyTorch实现神经网络

Posted on 2019-07-10 | In PyTorch , Machine Learning , Deep Learning

上一篇文章中我们用PyTorch实现了一个线性回归的模型，这篇文章我们将用神经网络来重新训练我们的模型。虽然我们只有一个feature和极为少量的训练样本，使用神经网络不免有些OverKill了，但使用神经网络的一个有趣之处是我们不知道它最后会帮我们拟合出的什么样的模型。

我们下面会用PyTorch搭建两个简单的神经网络来重新拟合上一篇文章中的模型，最后我们会做一个稍微复杂一点的全FC网络做图片分类。

一个神经元的神经网络

PyTorch中神经网络相关的layer称为module，封装在torch.nn中，由于我们的模型是线性的，我们可以用nn.Linear这个module，此外由于我们的例子中只有一个feature，加上我的输出也是一个值，因此我们的神经网络实际上只有一个神经元，输入是一个tensor，输出也是一个tensor。

import torch
import torch.nn as nn

t_x = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_x = torch.tensor(t_x).unsqueeze(1) #convert t_x to [11x1]
t_xn = t_x*0.1

linear_model = nn.Linear(1,1)
output = linear_model(t_xn)
print(output)

上述代码中我们创建了一个linear_model，这个model只有一个神经元，输入和输出只有一个tensor。接着我们创建了一个11x1的input tensor。由于我们的model没有经过训练，因此输出为一堆无意义的tensor。默认情况下nn.Linear包含bias，而weight值被初始化为一个随机数

print("weight: ",linear_model.weight) #tensor([[-0.1335]], requires_grad=True)
print("bias: ",linear_model.bias) #tensor([-0.4349], requires_grad=True)

接下来我们参考上一篇文章来训练我们的模型

optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
def train_loop(epochs, learning_rate, loss_fn,x, y):
    for epoch in range(1, epochs + 1):    
        optimizer.zero_grad()
        t_p = linear_model(x)
        loss = loss_fn(y, t_p)
        loss.backward()
        optimizer.step()
        print(f'Epoch: {epoch}, Loss: {float(loss)}')

上述代码中和前一节大同小异，有下面几点值得注意

待训练参数$\omega$和$b$保存在linear_model.parameters()中
由于params保存在了model中，因此PyTorch知道如何update这些参数，不再需要我们手动编写梯度下降的代码
loss函数使用系统自带的nn.MSELoss对应上一节的L2 loss函数

由于我们的linear_module在数学上就是在计算$y = \omega x + b$，我们可以猜到训练结果和前文是一致的

train_loop(3000, 1e-2, nn.MSELoss(),t_xn, t_y)
print("params:", list(linear_model.parameters()))
#tensor([[5.3491]], requires_grad=True), Parameter containing:
#tensor([-17.1995], requires_grad=True)]

训练结果符合我们预期，表面上看这个例子好像没什么意义，但它告诉我们可以使用神经网络来训练线性回归模型，在下一节我们将继续改进在这个简单的神经网络。

非线性模型

为了更精准的拟合数据，我们可以采用非线性模型，比如高阶的线性回归，但与其手动的定义模型，我们还是用神经网络帮我们寻找这个模型。不同的是这次我们要对数据做一些非线性变换，具体来说是引入一个hidder layer和activation函数。我们新的model结构如下

seq_model = nn.Sequential(
    nn.Linear(1,13),
    nn.Tanh(),
    nn.Linear(13,1))

print(seq_model)
# Sequential(
#   (0): Linear(in_features=1, out_features=13, bias=True)
#   (1): Tanh()
#   (2): Linear(in_features=13, out_features=1, bias=True)
# )

上述代码中我们引入了一个[1,13]的hidden layer，然后跟了一个Tanh()的非线性变换作为activation函数，最后的output layer又把结果变成[1,1]的tensor，整个model的结构如下图所示

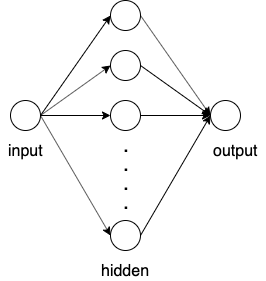
显然相比于前面的模型，这个模型略微复杂了一些。在训练我们的模型之前，我们先来分析下有多少个待学习参数。对于hidden layer我们有13个$\omega$，13个$b$，对于output layer，我们有一个$\omega$和一个$b$。因此一共有28个待学习的参数，我们也可以用下面代码来查看

for name,param in seq_model.named_parameters():
    print(name, param.shape)

# 0.weight torch.Size([13, 1])
# 0.bias torch.Size([13])
# 2.weight torch.Size([1, 13])
# 2.bias torch.Size([1])

上述代码会打印出整个network中待学习的参数。接下来我们用同样的思路训练我们的模型

optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)
def train_loop(epochs, learning_rate, loss_fn,x, y):
    for epoch in range(1, epochs + 1):    
        optimizer.zero_grad()
        t_p = seq_model(x)
        loss = loss_fn(y, t_p)
        loss.backward()
        optimizer.step()
        print(f'Epoch: {epoch}, Loss: {float(loss)}')

train_loop(5000, 1e-3, nn.MSELoss(),t_xn, t_y)

在5000次迭代后，loss收敛在1.950253963470459，接下来我们来可视化一下我们model并观察预测结果

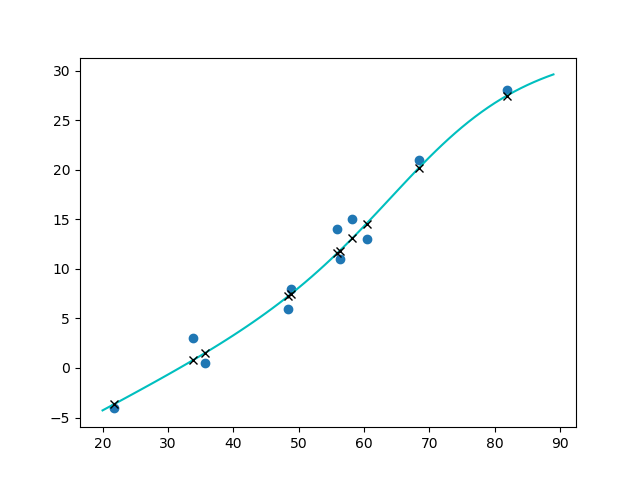
上图中实心的点为我们的原始数据，绿色的曲线是神经网络拟合出的曲线，标记为x的点为预测值。

可见相比于上一节的线性模型，我们训练出了一个非线性的预测函数，但实际上我们并不知道这个函数的具体公式是怎样的（虽然我们可以强行将神经网络展开，但是没有必要，我们只知道我们训练了28个参数，这也是神经网络比较神奇的地方。此外我们的hidden layer有13个neuron，这个值是随意指定的，我们也可以尝试增加更多的hidden layer和调整每个layer的神经元数量来达到更精准的拟合。

小结一下，这一节我们用PyTorch构建了一个两层的神经网络，训练了一个非线性模型，解决了一个简单的回归问题。但上述网络还是有些简单，在下面一节中我们将构建一个稍微复杂一点的网络来解决分类问题。

Fashion MNIST

这一节我们来设计一个稍微复杂一点的神经网络来解决图像识别的问题，我们要用的数据集是Fashion MNIST。数据集中的每个图片均为(28 * 28)的灰度图片，首先我们来准备数据

from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
                                transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('./F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)

# Download and load the test data
testset = datasets.FashionMNIST('./F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)

上述trainloader中包含了训练用的图片文件和标注，testloader存放我们的测试数据。transform的作用是对样本数据做Normalization。接下来我们遍历一下trainloader，观察训练数据的尺寸

print(len(trainloader)) #938
for images, lable in trainloader:
    print(images.shape) #torch.Size([64, 1, 28, 28])
    print(labels.shape) #torch.Size([64])

可以看到我们的训练集包含938组训练样本，每组样本的shape为[64,1,28,28]，表示每组64张图片，每张图只有一个channel，长宽均为28像素。

对于每一张图片来说，由于是灰度图片，只有一个通道，因此我们可以将输入的图片等价为一个[1x784]的一维向量，feature数量为像素点的个数。由于feature数量并没有很大，我们不需要引入卷积神经网络，使用若干层Fully Connected Layer（后面简称FC）堆叠即可。

FC (784,256)
ReLU()
FC (256,128)
ReLU()
FC (128,64)
ReLU()
FC (64,10)
Softmax()

和前面不同的是，这次我们要解决的是一个分类问题，因此我们的输出是Softmax(x)后的结果，这会直接影响我们的loss函数的选择。通常情况下，我们可以用nn.CrossEntropyLoss()。但根据文档

This criterion combines nn.LogSoftmax() and nn.NLLLoss() in one single class. The input is expected to contain scores for each class.

我们需要将FC的输出直接传给CrossEntropyLoss(),而不是softmax的输出。实际应用中，我们更希望将两者分开，因此这里我们使用nn.NLLLoss()。确定了loss函数后，我们可以测试下我们的model

class Classifier(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 128)
        self.fc3 = nn.Linear(128, 64)
        self.fc4 = nn.Linear(64, 10)
        # Dropout module with 0.2 drop probability
        self.dropout = nn.Dropout(p=0.2)

    def forward(self, x):
        x = x.view(x.shape[0], -1) #convert the input tensor to [64,784]
        x = self.dropout(F.relu(self.fc1(x)))
        x = self.dropout(F.relu(self.fc2(x)))
        x = self.dropout(F.relu(self.fc3(x)))
        x = F.log_softmax(self.fc4(x), dim=1)

        return x

model = Classifier()
images,labels = next(iter(trainloader))
output = model(images)

这里需要注意的是，对于nn.LogSoftmax我们需要指定dim的值，dim=1表示按row进行sum。我们可以观察一模型的输出

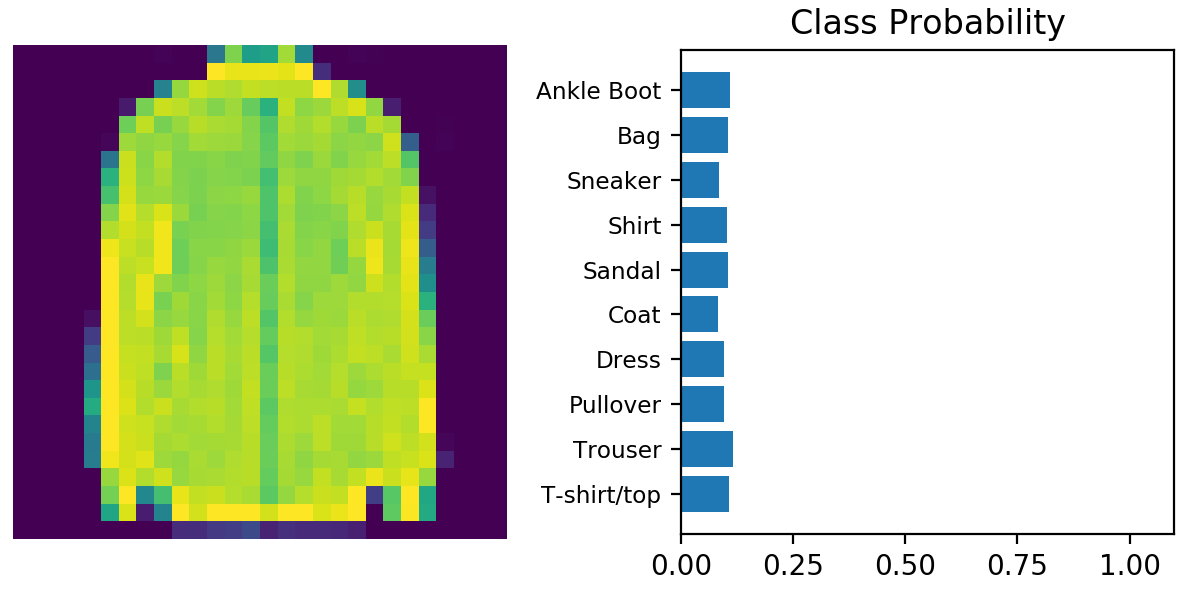
由于我们的模型还未经训练，因此输出结果基本可以认为是等概率分布，接下来我们按照前面的方法来train我们的模型

loss_fn = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 5
for e in range(epochs):
    running_loss = 0
    for images, labels in trainloader:
        optimizer.zero_grad()
        outputs = model(images)
        loss = loss_fn(outputs,labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    else:
        print(f"Traning loss: {running_loss}")

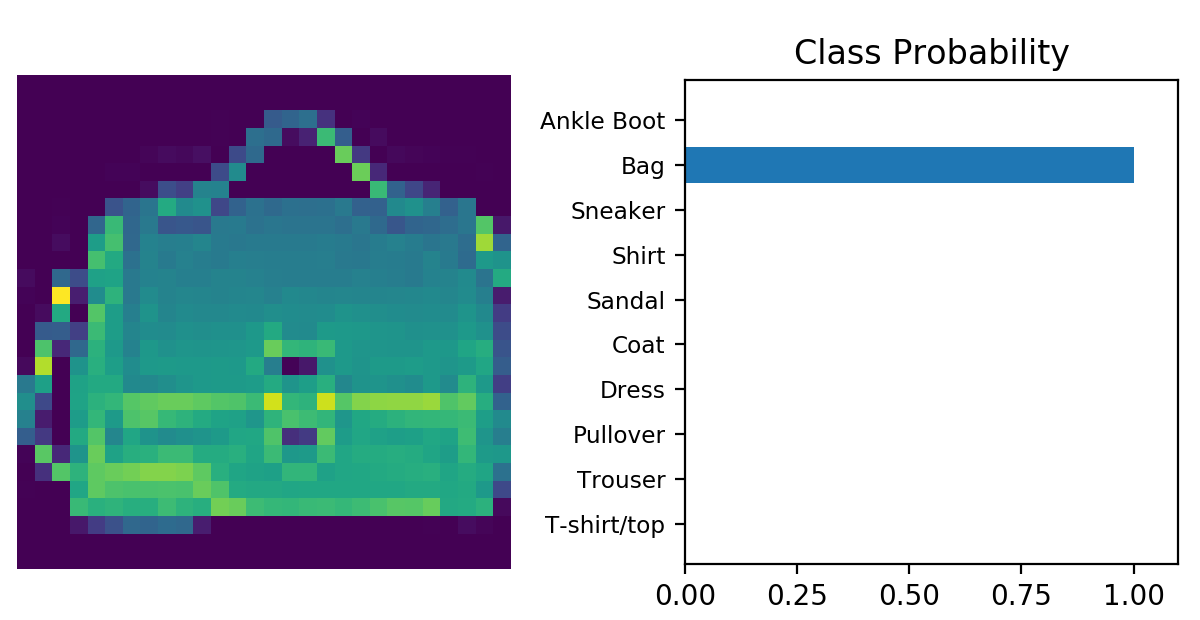
迭代5次后Loss收敛在0.317，此时我们跑一张测试集的图片，并观察输出结果

解决过拟合问题

从上图中看，貌似我们的模型还不错，但是我们需要一个量化指标来衡量模型的准确率，常见的做法是在每一个training loop结束时，用我们的测试集测试一次并观察输出结果。由于每一张图片会产生10个结果，我们只取概率最高的一项，而一次loop有64张图片，因此我们的结果是一个[64,1]的向量。

为了得到上述结果我们要用到PyTorch中的topk函数，这个函数会返回概率由高到低的前k个结果，对于我们的场景，我们只需要返回第一个，因此用topk(1,dim=1)即可。另外由于我们要将预测结果和测试集中的label做比较，因此我们需要确保这两个tensor的size是一致的

images, labels = next(iter(testloader))
output = torch.exp(model(images)) #convert the output tensor to [0,1]
top64 = output.topk(1,dim=1) #[64,1]
labels = labels.view(64,-1) #convert labels to [64.1]

上述代码可以确保我们的输出结果可以和label的size一致。接下来我们要计算准确率，方法很简单，用比较结果为true的数量除以结果数量（10）即可，我们可以使用torch.mean

equals = top64 == labels
accuracy = torch.mean(equals.type(torch.FloatTensor))

有了上面的铺垫，现在我们可以在训练中加入validation的代码

test_loss = 0 
accuracy = 0
with torch.no_grad():
    for images, labels in testloader:
        log_ps = model(images)
        test_loss += loss_fn(log_ps, labels) #计算test_loss
        ps = torch.exp(log_ps)
        top_p, top_class = ps.topk(1, dim=1)
        equals = top_class == labels.view(top_class.shape[0],-1) 
        accuracy += torch.mean(equals.type(torch.FloatTensor)) #计算accuracy

train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))

print("Epoch: {}/{}.. ".format(e+1, epochs),
        "Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
        "Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
        "Test Accuracy: {:.3f}".format(accuracy/len(testloader)))

这一次我们增加了epochs值为30，然后观察Training Loss和Test Loss两个指标的变化情况，如下图所示

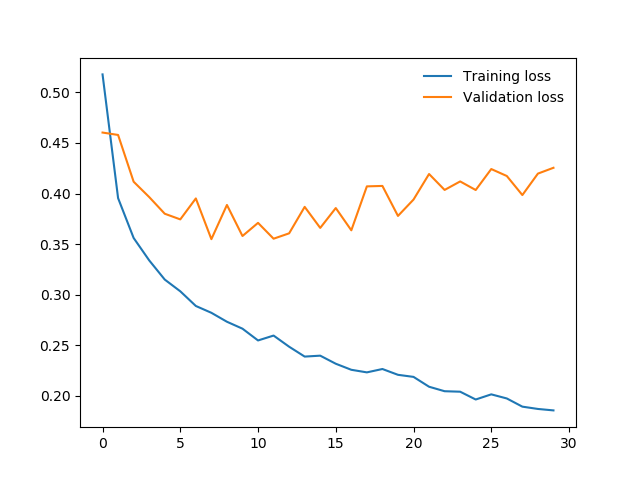
显然我们的模型出现了过拟合，即training error不断降低，但是testing error却不降反升。为了解决过拟合，常用手段是引入Dropout层，即对参数做Regularization。修改我们的model，加入dropout

class Classifier(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 128)
        self.fc3 = nn.Linear(128, 64)
        self.fc4 = nn.Linear(64, 10)
        # Dropout module with 0.2 drop probability
        self.dropout = nn.Dropout(p=0.2)

    def forward(self, x):
        x = x.view(x.shape[0], -1)
        x = self.dropout(F.relu(self.fc1(x)))
        x = self.dropout(F.relu(self.fc2(x)))
        x = self.dropout(F.relu(self.fc3(x)))
        x = F.log_softmax(self.fc4(x), dim=1)

        return x

引入Dropout之后我们还需要修改一下训练代码，当我们对测试数据做forward的时候，需要禁掉Dropout，我们要调一下model.eval()，而在下次training开始前，我们再调一下model.train()来开启Dropout，代码如下

with torch.no_grad():
        model.eval() #disable dropout
        for images, labels in testloader:
            ...
            #validation code
            ...
model.train()#enable dropout

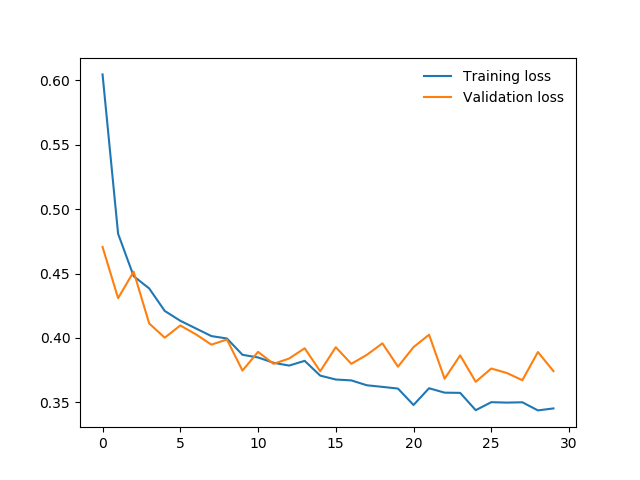
重新训练，观察上述两个指标的变化情况，如下图所示。基本上我们可以认为我们的模型可以正常工作了。

小结

这个例子中我们训练了一个相对复杂一点的神经网络，并解决了一个图片分类的问题。我们使用Fully Connected Layer作为hidden layer，通过Softmax对结果分类。需要注意的是，我们的模型并不是一个CNN模型，而是将像素点全部打散后将每个像素点作为一个单独的feature。这种实际上损失了图片在spatial方面的信息，只适用于识别简单的，分辨率低的图片。对于复杂高分辨率的图片，需要使用CNN来构建模型

总结一下上面的步骤

准备数据，并可视化。这一步可以使用PyTorch的datasets和torch.utils.data.DataLoader
对数据做预处理，这一步可以使用PyTorch的transforms
设计model
选取Optimizer和loss函数，训练
观察training error和validation error，并在validation error区域稳定时停止training
用测试集测试我们的model

PyTorch实现神经网络

一个神经元的神经网络

非线性模型

Fashion MNIST

解决过拟合问题

小结

Resoures