Storage Allocation
Stack Storage
Array and pointer
A ----used----- ------unused----
|
sp
# Allocate x bytes
sp += x
return sp-x
- Allocating and freeing take
O(1)time. - Must free consistent with stack discipline
- Limited applicability, but great when it works
- One can allocate on the call stack using
alloca(), but this function is deprecated, and the compiler is more efficient with fixed-size frames.
Limitation: there is no way to free memory in the middle of the used-region on the stack. ONly the last object can be freed.
Heap
C provides malloc() and free(). C++ provides new and delete.
Unlike Java and Python, C and C++ provide no garbage collectors. Heap storage allocated by the programmer must be freed explicitly. Failure to do so can creates a memory leak. Also, watch for dangling pointers and double freeing
Memory checkers (e.g. AddressSanitizer, Valgrind) can assist in finding these pernicious bugs.
Fixed-size Allocation
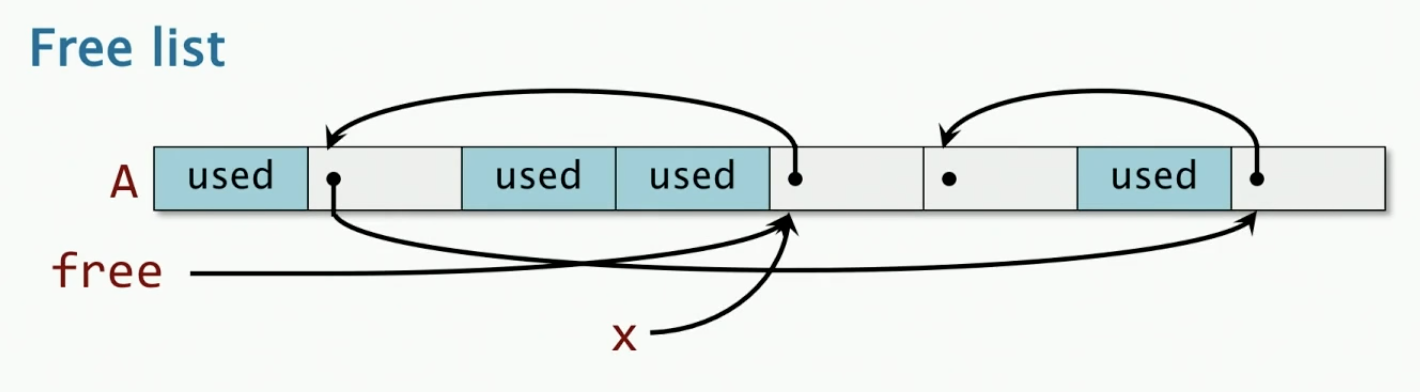
- Every piece of storage has the same size
- Unused storage has a pointer to next unused block
Allocate 1 object
x = free;
free = free->next;
return x;
Fixed-size Deallocation
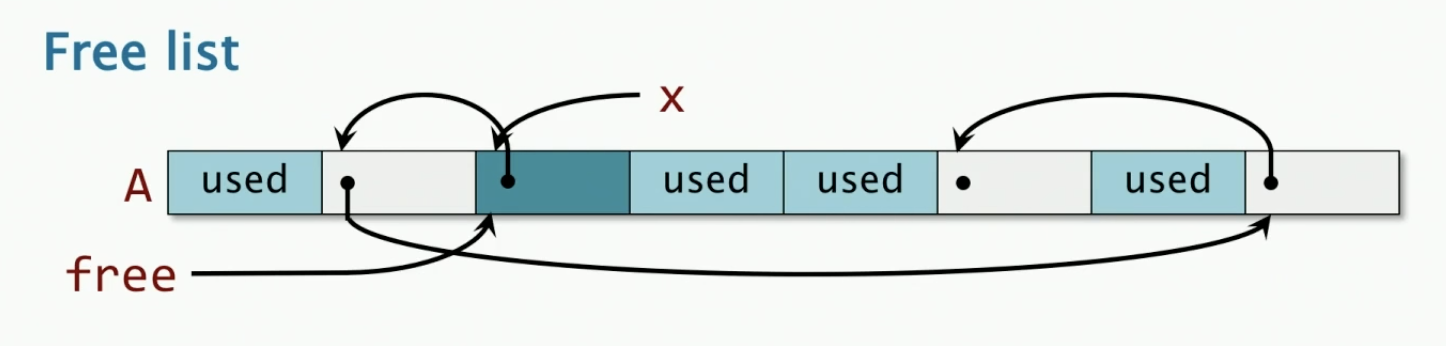
free object x
x->next = free;
free = x
- Allocating and freeing take
O(1)time - Good temporal locality
- Poor spatial locality due to external fragmentation - blocks distributed across virtual memory - which can increase the size of the page table and cause disk thrashing (page fault)
- THe translation lookaside buffer(TLB) can also be a problem (map virtual address to physical address)
Mitigating External Fragmentation
- Keep a free list per disk page.
- Allocate from the free list for the fullest page.
- Free a block of storage to the free list for the page on which the block resides.
- If a page becomes empty(only free-list items), the virtual-memory system can page it out without affecting program performance
- 90-10 is better than 50-50

Probability that 2 random accesses hit the same p age = .9 x .9 + .1 x .1 = .82 vs .5 x .5 + .5 x .5 = .5
Variable-Size Allocation
Binned free lists
- Leverage the efficiency of free lists
- Accept a bounded amount of internal fragmentation
- Each bin is going to store a particular size

Allocate x bytes
- If bin
k=[lg x](以2为底log向上取整) is nonempty, return a block. - Otherwise, find a block in the next larger nonempty bin
k' > k, split it up into blocks of size $2^{k^’-1}, 2^{k^’-2}, 2^{k^’-3}, … ,2^{k}, 2^{k}$, and distribute the pieces.
Note that we’ll have two $2^{k}$, one of them will be returned.
For example, x=3, k = log[x] = 2. Bin 2 is empty
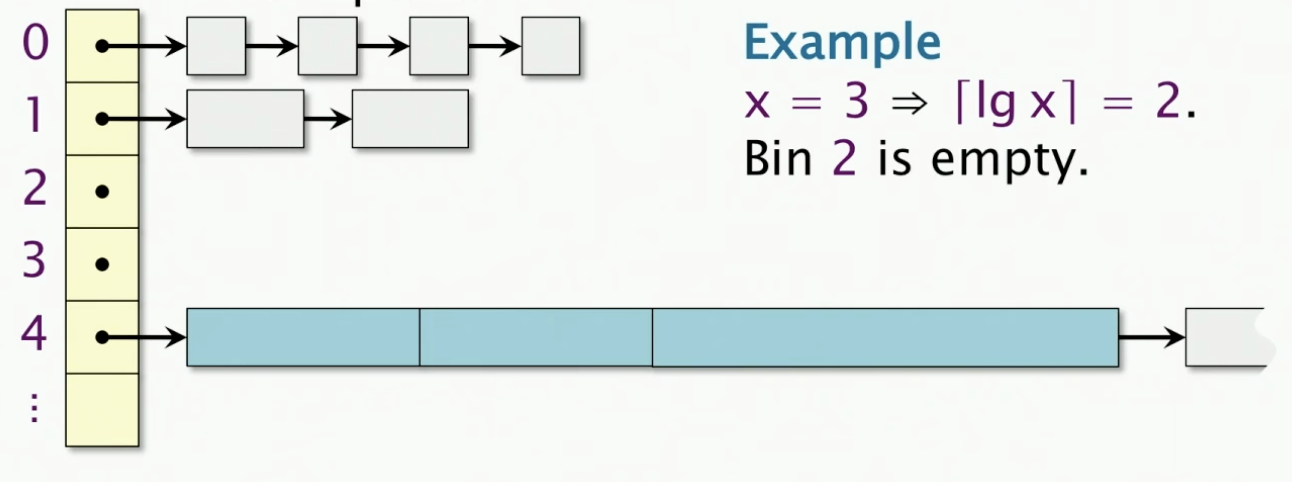
So we are going to look for a non-empty bin, which is 4 in this case. so k' = 4.
Next, we’ll split the block into 2^(3), 2^(2), 2^(2) and return 2^(2) = 4, as shown below.
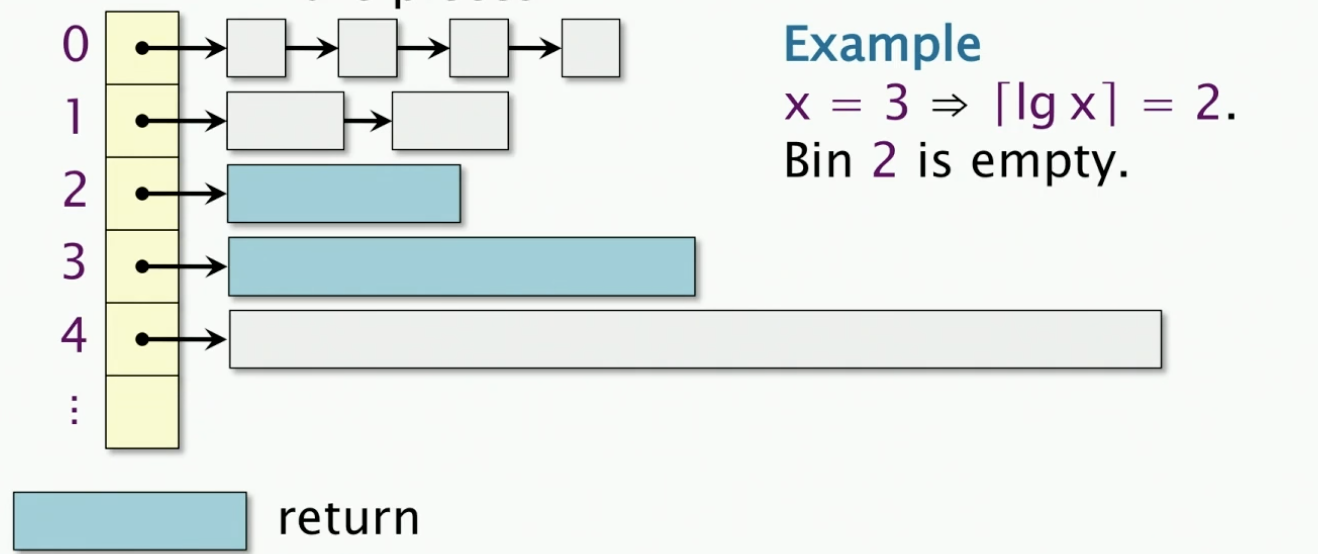
if no larger blocks exist, ask the OS to allocate more memory.
mmap,sbrkthose are system calls for asking memory
In practice, this exact scheme isn’t used. There are many variants. It turns out that the efficiency is very important for small allocations. The overhead of this scheme could cause performance bottlenecks. In reality, we usually don’t go all the way down to the block of size 1. We might stop at block of size 8 bytes. This does increase internal fragmentations because we have some waste space.
Alternatively, we can also group blocks into pages. All of blocks in the same page have the same size.
The standard implementation of malloc uses mmap andd sbrk to allocate memory. It doesn’t use any memory allocator.
Analysis of Binned Free Lists
Theorem. Suppose that the maximum amount of heap memory in use at any time by a program is M. If the heap is managed by a BFL allocator, the amount of virtual memory consumed by heap storage is O(MlgM)
Proof. An allocation request for a block of size x consumes 2^{lg[x]} <= 2x storage. Thus, the amount of virtual memory devoted to blocks of size 2^k is at most 2M. Since there are most lgM free lists, the theorem holds.
Storage Layout of a program
This is how the virtual memory address space is laid out.
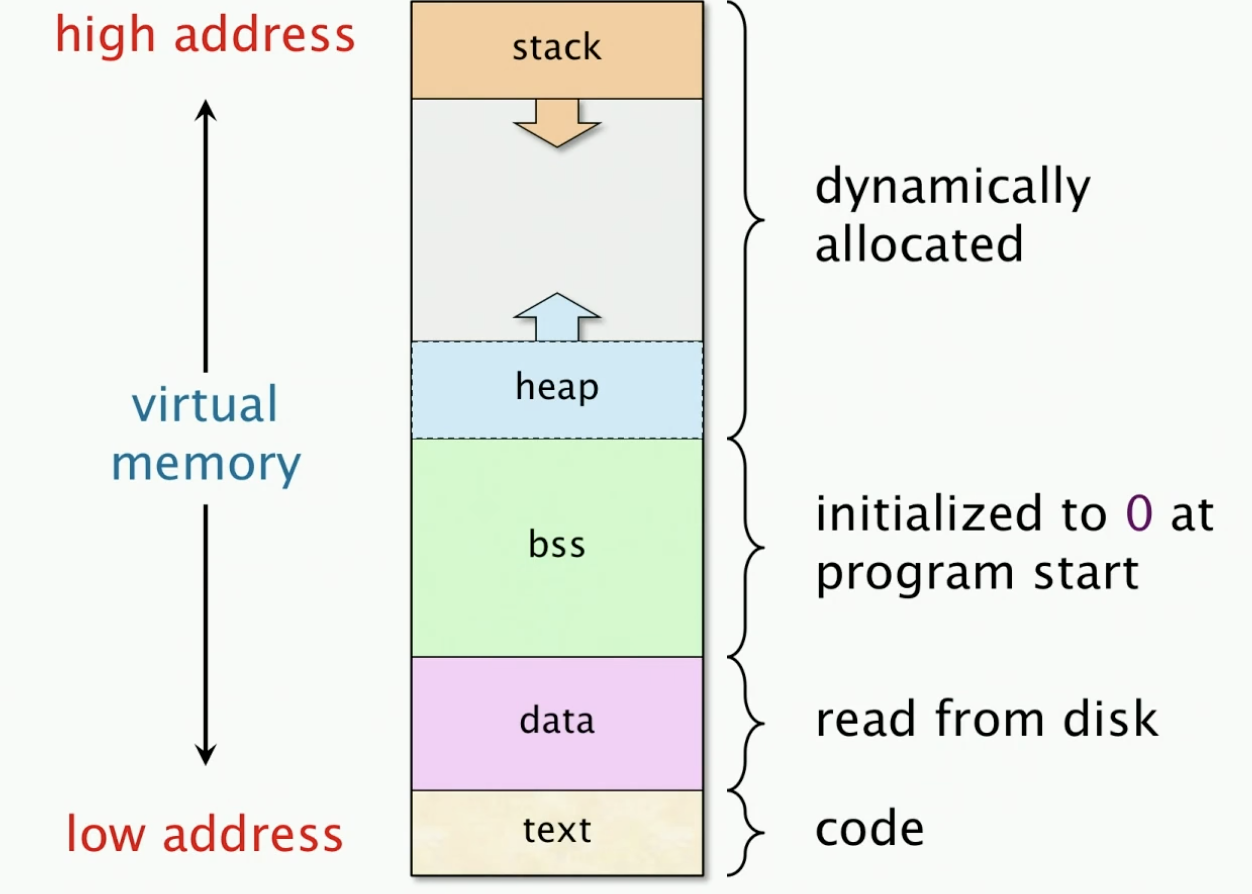
In practice, the stack and heap pointer are never going to hit each other because we’re working with 64bit addresses.
How virtual is virtual memory
Q: Since a 64-bit addressed space takes over a century to write at rate of 4 billion bytes per second, we effectively never run out of virtual memory. Why not just allocate out of virtual memory and never free?
A1: Will be running out of physical memory
A2: External fragmentation would be horrendous! The performance of the page table would degrade tremendously leading to disk thrashing, since all nonzero memory must be backed up on disk in page-size blocks.
Goal of storage allocators
Use as little virtual memory as possible, and try to keep the used portions relatively compact.
Garbage Collection
Terminology
- Roots are objects directly accessible by the program (globals, stack, etc.).
- Live objects are reachable from the roots by following pointers.
- Dead objects are inaccessible and can be recycled.
In order for GC to work, in general, you need to have the GC identify pointers, which requires
- Strong typing.
- Prohibit pointer arithmetic (which may slow down some programs). Beacuse if the program changes the location of the pointer, then GC no longer knows where the memory region starts anymore.
Reference Counting
Keep a count of the number of pointers referencing each object. If the count drops to 0, free the dead object.
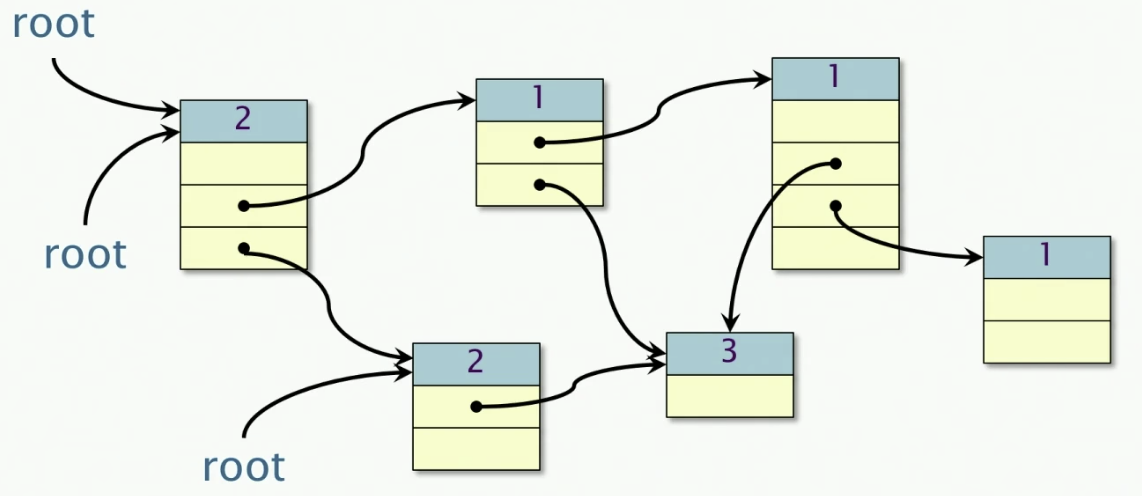
A retain cycle is never garbage collected!
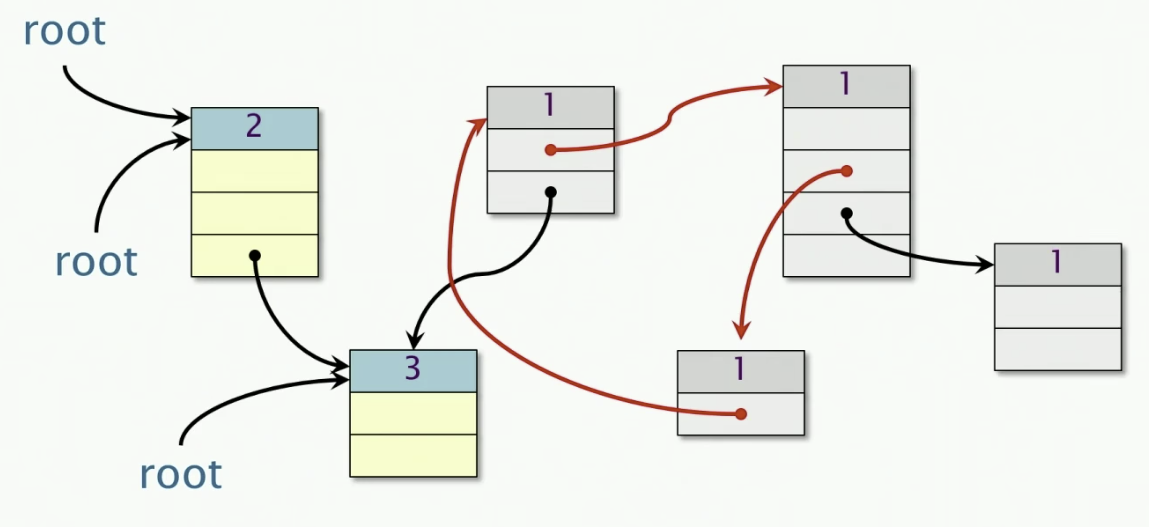
Objective-C solves this issue by introducing a two specical pointers, namely strong pointers and weak pointers. The reference count only stores the incoming of strong pointers. The weak pointers don’t contribute to the ref count.
Mark-and-Sweep GC
Define a Graph Abstraction
Objects and pointers from a directed graph G = (V,E). Live objects reachable from the roots. Use BFS to find the live objects.
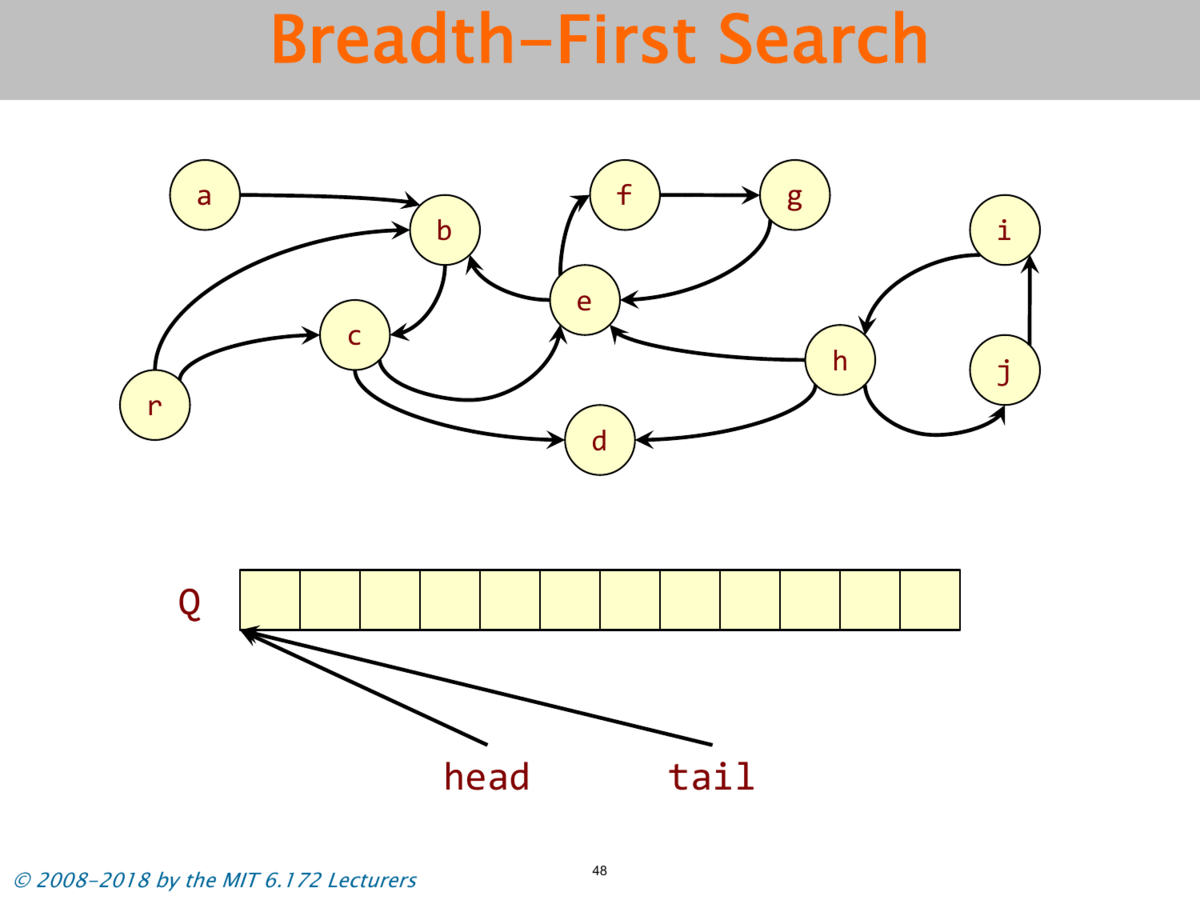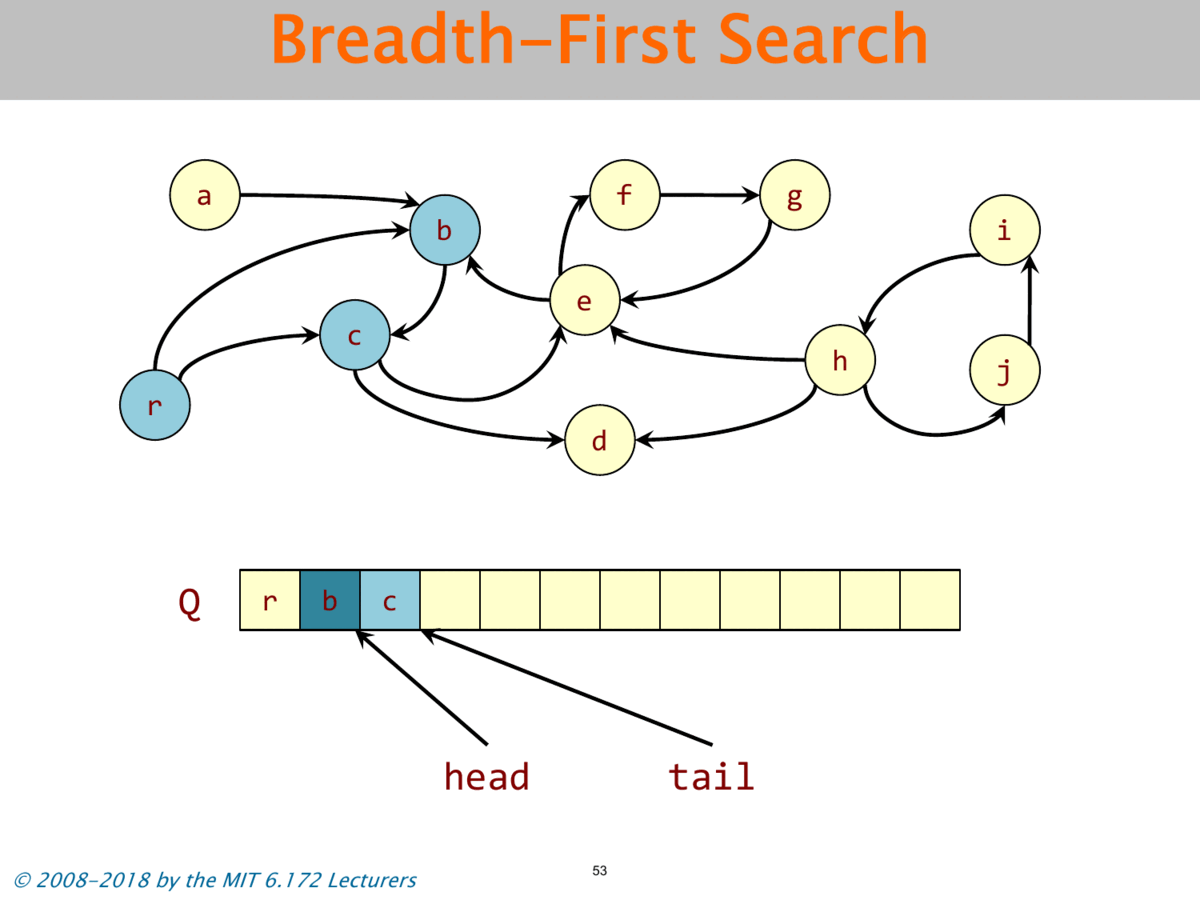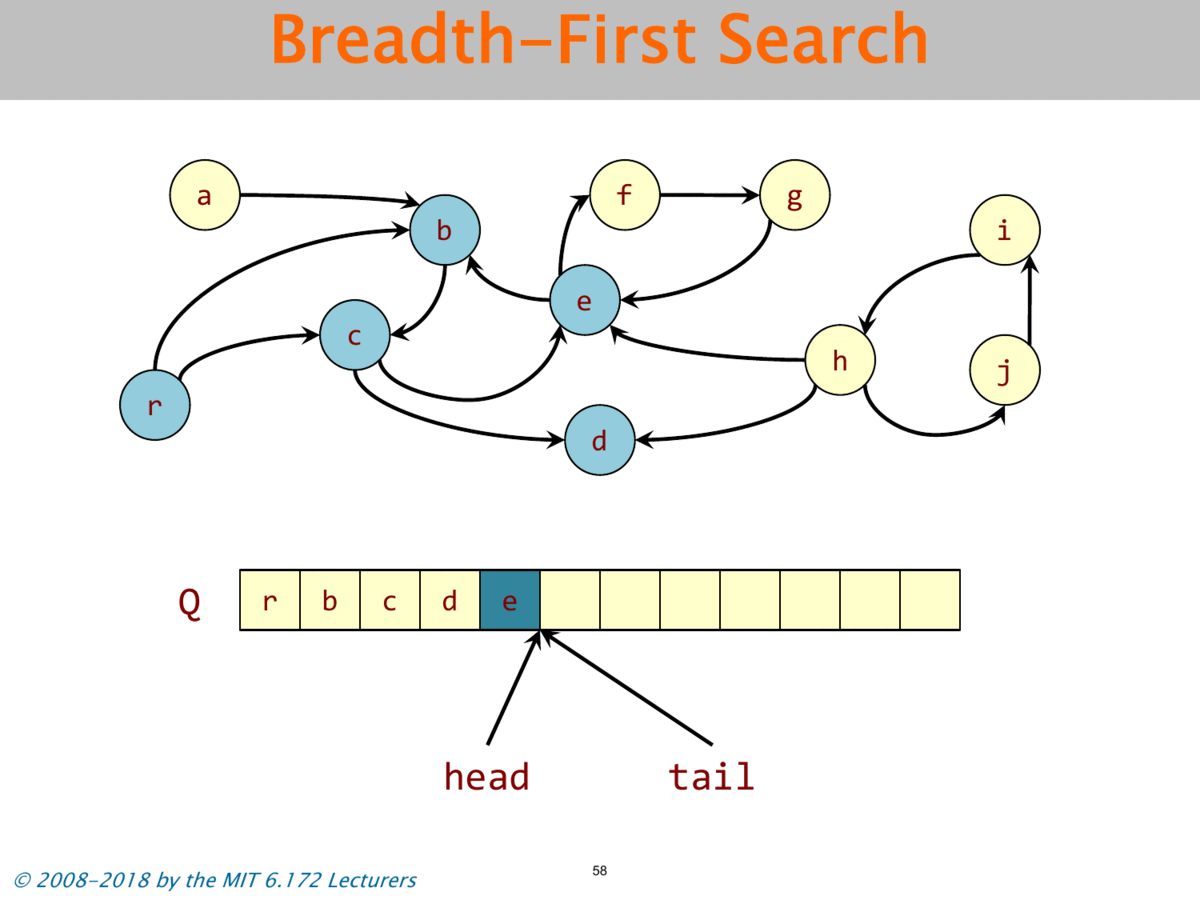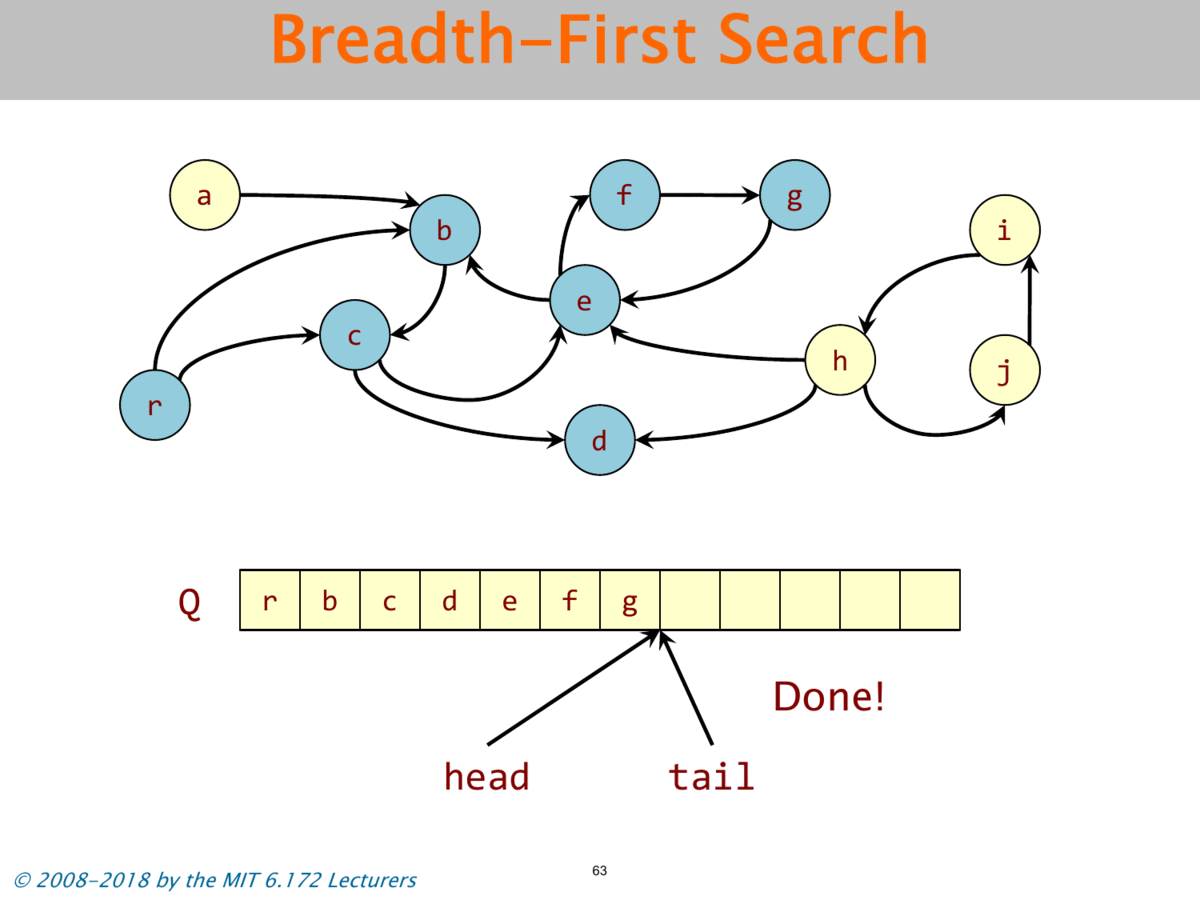
# seudo code
queue<vertex> Q;
for (v : vertices) {
if (root(v)) {
v.mark = 1;
enqueue(Q, v);
} else {
v.mark = 0;
}
}
while(!Q.empty()){
u = dequeue(Q);
for (v : v.children) {
if(v.mark == 0){
v.mark = 1;
enqueue(Q, v);
}
}
}
The Mark and Sweep procedures has two stages
- Mark Stage: Breadth-first search marked all of live objects
- Sweep Stage: Scan over memory to free unmarked objects
Mark-and-sweep doesn't deal with fragmentation. It doesn’t compact the live objects to be contiguous in memory. It just frees the ones that are unreachables. It doesn’t do anything with the ones that are reachable.
Stop-And-Copy GC
At a higher level, it is similar to Mark-And-Sweep GC. It uses BFS to identify the live objects. Since all vertices are placed in contiguours storage in Q, we can use our queue as new memory. All unreachable objects will be implicitly deleted. This procedure will deal with external fragmentation.
Linear time to copy and update all vertices.
