Basic Concepts of Quantization

Introduction

Quantization refers to the process of mapping a large set to a smaller set of values. It is a widely used model compression technique that reduces the memory footprint and computational costs of deep learning models. For example, in an 8-bit quantization process, a 32-bit float number(torch.float32) will be mapped to an 8-bit integer (torch.int8) in the memory.

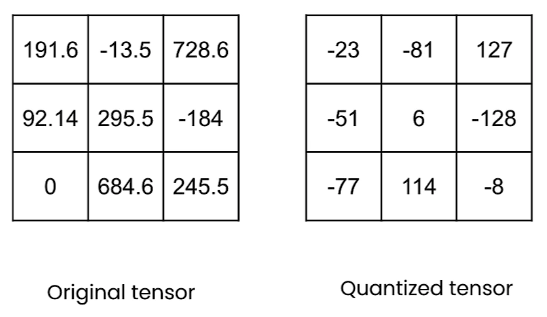
In a typical neural network, quantization can be applied to quantize the model weights and the activations. When quantization is applied after the model has been fully trained, it is referred to as post-training quantization (PTQ).

The advantages of quantization include:

• Smaller model
• Speed gains
  • Memory bandwidth
  • Faster operations
    • GEMM: matrix to matrix multiplication
    • GEMV: matrix to vector multiplication

Linear Quantization

Linear Quantization uses a linear mapping to map a higher precision range(e.g. float32) to a lower precision range(e.g. int8) with a fixed scaling factor and zero point. This ensures that floating-point numbers are effectively represented in a lower precision format with minimal information loss.

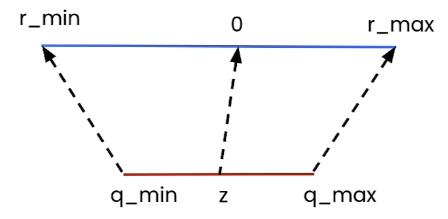
The linear mapping formula can be described as:

Where $r$ is the original value(e.g. fp32), $q$ is the quantized value(e.g. int8), $s$ is scale and $z$ is the zero point. For example, with $s=2$ and $z=0$, we get $r = 2(q-0) = 2q$. If $q = 10$, then we have $r = 2 \times 10 = 20$.

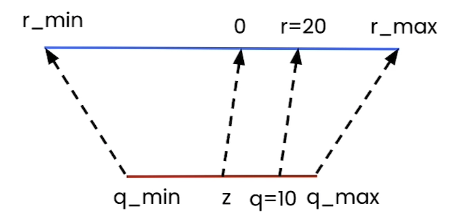
The formula for calculating $q$:

PyTorch’s implementation:

import torch

def linear_q_with_scale_and_zero_point(
    tensor, scale, zero_point, dtype = torch.int8):
    scaled_and_shifted_tensor = tensor / scale + zero_point
    rounded_tensor = torch.round(scaled_and_shifted_tensor)

    q_min = torch.iinfo(dtype).min # -128
    q_max = torch.iinfo(dtype).max # 128
    q_tensor = rounded_tensor.clamp(q_min,q_max).to(dtype)
    
    return q_tensor

def linear_dequantization(quantized_tensor, scale, zero_point):
    return scale * (quantized_tensor.float() - zero_point)

Note that if we pick up a random scale and zero_point number, the quantized error could be really high. So how do we determine $s$ and $z$? If we look at the extreme values for $[r_{min}, r_{max}]$ and $[q_{min}, q_{max}]$, we should have:

If we subtract the first equation from the second one, we get the scale:

For the zero point, we need to round the value since it is a n-bit integer

def get_q_scale_and_zero_point(tensor, dtype=torch.int8):
    q_min, q_max = torch.iinfo(dtype).min, torch.iinfo(dtype).max
    r_min, r_max = tensor.min().item(), tensor.max().item()

    scale = (r_max - r_min) / (q_max - q_min)
    zero_point = q_min - (r_min / scale)

    # clip the zero_point to fall in [quantized_min, quantized_max]
    if zero_point < q_min:
        zero_point = q_min
    elif zero_point > q_max:
        zero_point = q_max
    else:
        # round and cast to int
        zero_point = int(round(zero_point))
    
    return scale, zero_point

To put everything together, we now have one single function to quantize a tensor:

def linear_quantization(tensor, dtype=torch.int8):
    scale, zero_point = get_q_scale_and_zero_point(tensor, dtype=dtype)
    quantized_tensor = linear_q_with_scale_and_zero_point(
        tensor,
        scale, 
        zero_point, 
        dtype=dtype)
    
    return quantized_tensor, scale , zero_point

Symmetric vs Asymmetric mode

There are two modes in linear quantization:

• Asymmetric: map $[r_{min}, r_{max}]$ to [$q_{min}$, $q_{max}$]. This is what we implemented in the previous section.
• Symmetric: map $[-r_{max}, r_{max}]$ to [$-q_{max}$, $q_{max}$], where $r_{max} = max(|tensor(r)|)$

In the symmetric mode, we don’t need to use the zero point(z = 0). This is because the floating-point range and the quantized range are symmetric with respect to zero.

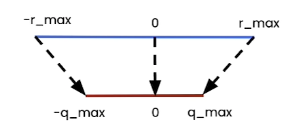
Hence, we can simplify the equation to

PyTorch’s implementation for calculating scale:

def get_q_scale_symmetric(tensor, dtype=torch.int8):
    r_max = tensor.abs().max().item()
    q_max = torch.iinfo(dtype).max

    # return the scale
    return r_max/q_max

Once we have the scale value calculated, we can reuse the function in the asymmetric mode to get the quantized tensor.

def linear_quantization(tensor, dtype=torch.int8):
    scale = get_q_scale_symmetric(tensor, dtype=dtype)
    quantized_tensor = linear_q_with_scale_and_zero_point(
        tensor,
        scale, 
        0,  # zero_point = 0
        dtype=dtype)
    
    return quantized_tensor, scale

The trade-off between symmetric and asymmetric mode of quantization are:

• Utilization of quantized range:
  • When using asymmetric quantization, the quantized range is fully utilized.
  • When symmetric mode, if the float range is biased towards one side, this will result in a quantized range where a part of the range is dedicated to values that we’ll never see. (e.g., ReLU where the output is positive).
• Simplicity: Symmetric mode is much simpler compared to asymmetric mode.
• Memory: We don’t store the zero-point for symmetric quantization.

In practice, when quantizing to 8 bits, we often use symmetric quantization. However, when quantizing to fewer bits (e.g., 4 bits, 2 bits), we prefer to use asymmetric quantization.

Finer Granularity for more Precision

In addition to per-tensor quantization, we can also do per-channel and per-group quantization, as shown below

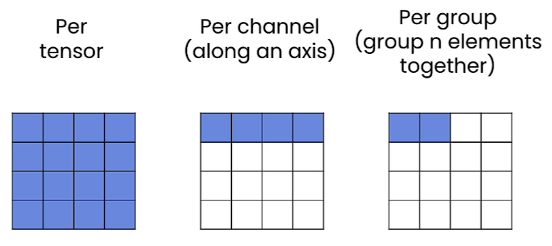
The idea is that we don’t have to use the same scale and zero-point for every tensor. Instead, we can divide tensor in multiple group and apply different scale and zero-point to each group.

Per-Channel Quantization

We usually use per-channel quantization when quantizing models in 8 bits. In PyTorch, we can use tensor.shape[dim] to grab the channel we want to quantize. For example, for a torch.Size([2, 3]) tensor, if we set the dim = 0, we will get 2 from the shape value, meaning we will quantize the two rows of the tensor. In symmetric quantization, this also means we need two scales, one for each row.

def linear_q_symmetric_per_channel(r_tensor, dim, dtype=torch.int8):
    # r_tensor is [2,3]
    output_dim = r_tensor.shape[dim]
    # store the scales
    scale = torch.zeros(output_dim)

    for index in range(output_dim):
        sub_tensor = r_tensor.select(dim, index) # this gives you a [1, 3] tensor
        scale[index] = get_q_scale_symmetric(sub_tensor, dtype=dtype)

    # scale is a 1x2 tensor, [s1, s2], to let each row divided by s[i], we need to reshape
    # the scale tensor in a column order (a 2x1 tensor):
    # [s1,
    #  s2]
    #
    scale_shape = [1] * r_tensor.dim()
    scale_shape[dim] = -1
    # reshape the scale
    scale = scale.view(scale_shape)
    quantized_tensor = linear_q_with_scale_and_zero_point(
        r_tensor,
        scale=scale,
        zero_point=0,
        dtype=dtype)
   
    return quantized_tensor, scale

Per-Group Quantization

In per-group quantization, we perform group quantization in a group of N elements. The common values for N are 32, 64 or 128.

Per-group quantization can require a lot more memory. Let’s say we want to quantize a tensor in 4-bit, and we choose group_size = 32, symmetric mode (z=0), and we store the scales in FP16.

It means that we’re actually quantizing the tensor in 4.5 bits since we have:

• 4 bit (each element is stored in 4 bit)
• 16/32 bit (scale in 16 bits for every 32 elements)

def linear_q_symmetric_per_group(
    tensor, 
    group_size,
    dtype=torch.int8):
    
    t_shape = tensor.shape
    assert t_shape[1] % group_size == 0
    assert tensor.dim() == 2
    
    # reshape the tensor to [n, group_size]
    tensor = tensor.view(-1, group_size)
    
    # quantize the tensor per-row
    quantized_tensor, scale = linear_q_symmetric_per_channel(
                                tensor, 
                                dim=0, 
                                dtype=dtype)
    
    # restore the shape of the quantized tensor
    quantized_tensor = quantized_tensor.view(t_shape)
    
    return quantized_tensor, scale

Quantizing weights & activation for inference

Quantization can be applied to both weights and activations. When both are quantized, inference is performed using integers (e.g., int8, int4). Currently, this is not supported by all hardware products.

If only the weights are quantized, inference remains in floating-point precision (e.g., fp32, fp16, bf16). However, we need to quantize the weights first before performing the floating point computation.

def quantized_linear_W8A32_without_bias(input, q_w, s_w, z_w):
    assert input.dtype == torch.float32
    assert q_w.dtype == torch.int8

    # w = scale * (q_w - zero_point)
    dequantized_weight = s_w * (q_w.to(torch.float32)  - z_w)
    output = torch.nn.functional.linear(input, dequantized_weight)
    
    return output

def main():
    x = torch.tensor([[1, 2, 3]], dtype=torch.float32) # [1,3]
    weight = torch.rand(3, 3) #[3, 3]
    q_w,s_w = linear_quantization(weight)
    y = quantized_linear_W8A32_without_bias(x, q_w, s_w, 0)
    print(y)

Now we are familiar with the basic concepts of quantization. In the next article, we are going to use everything we learned here to build a custom 8-bit quantizer.

Resource

• Quantization in Depth