首页 | Home
博客 | Blog
关于 | About

Cross Attension Unet

Posted on | In GenAI , Stable Diffusion

Attention U-Net (Conditioning via Cross-Attention)

From the last two sections we know that the CLIP model encodes the prompts into text embeddings in the CLIP space, and the VAE encodes the noise image into latent vectors in the latent space. Since these two lives in different higher dimensional space, how does the text embedding affect the latent vectors? To answer this question, we are going to dive deep into the U-Net architecture.

The traditional U-Net is a U shape architecture commonly used in image semantic segmentation tasks. To support the conditional image generation, Stable Diffusion adds cross-attention modules, which is effective for learning attention-based models of various input modalities.

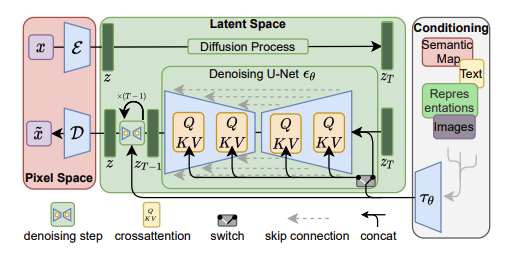
The U-Net architecture used in Stable Diffusion 1.5 can be found here. At various layers in the encoder path, the latent image features (z) are processed using ResNet blocks and cross-attention blocks. In each cross-attention block:

  • The query is the current latent vectors ([B, HxW, C])
  • The key and value come from the CLIP text embeddings ([B, 77, 768])

Similar to the transformer blocks in LLM, the cross-attention U-Net computes the attention score between image patches (latent vectors) and text embeddings via dot products:

\[\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{QK^\top}{\sqrt{d}} \right) V\]

This allows each patch in the image (latent vectors) to "look at" what part of the text is most relevant, and pull that information in (e.g., “a red car” → pulls “red” and “car” info to guide denoising).

However, if we look closely, in each Transformer2DModel, we actually have two attention modules - self-attention and cross-attention:

(attn1): Attention(
    to_q: Linear(in_features=320, out_features=320, ...)
    to_k: Linear(in_features=320, out_features=320, ...)
    to_v: Linear(in_features=320, out_features=320, ...)
)

(attn2): Attention(
    to_q: Linear(in_features=320, out_features=320, ...)
    to_k: Linear(in_features=768, out_features=320, ...)  # CLIP text embedding input!
    to_v: Linear(in_features=768, out_features=320, ...)
)
  • The self-attention module lets the image patches (latent vectors) learn context from its neighbors(similar to LLM ‘s). This is important because it helps generate patches that stay consistent with nearby regions
  • The cross-attention module shifts the latent vectors to the desired location in the latent space by attending the text embedding from the input tokens.

Appendix #3 demonstrates the computation process inside attn1 and attn2.

Training the Attention U-Net

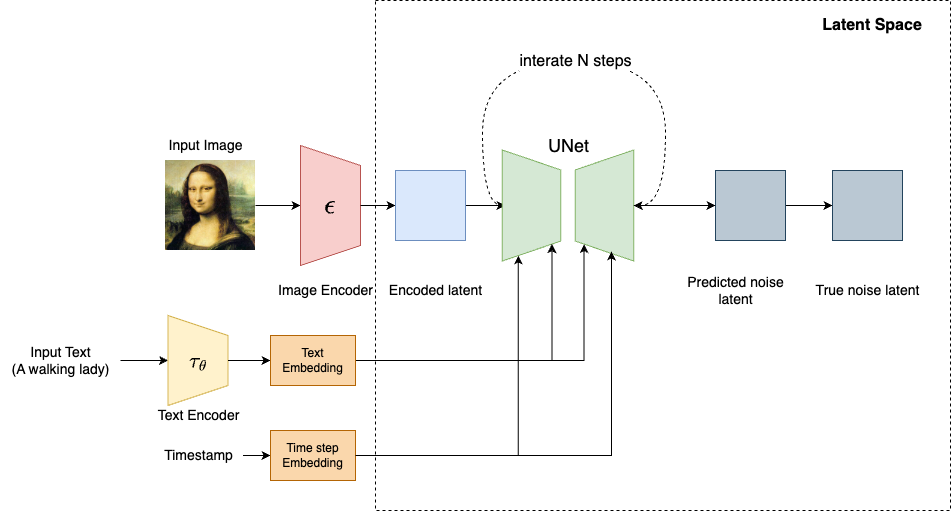
Training the attention U-Net model is similar to training the diffusion model outlined in the previous post. The major difference is that we now have (text, image) pairs as our training data.

  • Start with an image and caption, e.g. “a cat wearing sunglasses on a beach”
    • Convert the image to a latent representation using the VAE encoder → $z_{\theta}$
    • Encode the text prompt using CLIP → text_embedding
  • Add noise to latent
    • Sample a time step $t$ from the noise schedule.
    • Add Gaussian noise to $z_{\theta}$ to get $z_t$ using the same following formula, Where $\epsilon$ is standard Gaussian noise:
    \[z_t = \sqrt{\alpha_t} \cdot z_0 + \sqrt{1 - \alpha_t} \cdot \varepsilon\]
  • Predict the noise with U-Net
    • The noisy latent $z_t$ is passed into the U-Net
    • The U-Net is conditioned on the text embedding (via cross-attention)
    • The U-Net tries to predict the noise $\varepsilon_\theta$

  • Compute the loss as follows

    \[\mathcal{L} = \left\| \varepsilon_\theta - \varepsilon \right\|^2\]

Resources

Appendix: Cross Attention U-Net

Below is the architecture of Transformer2DModel, which is heart and soul of the cross-attention U-Net.

(attentions): ModuleList(
    (0-1): 2 x Transformer2DModel(
      (norm): GroupNorm(32, 320, eps=1e-06, affine=True)
      (proj_in): Conv2d(320, 320, kernel_size=(1, 1), stride=(1, 1))
      (transformer_blocks): ModuleList(
        (0): BasicTransformerBlock(
          (norm1): LayerNorm((320,), eps=1e-05, elementwise_affine=True)
          (attn1): Attention(
            (to_q): Linear(in_features=320, out_features=320, bias=False)
            (to_k): Linear(in_features=320, out_features=320, bias=False)
            (to_v): Linear(in_features=320, out_features=320, bias=False)
            (to_out): ModuleList(
              (0): Linear(in_features=320, out_features=320, bias=True)
              (1): Dropout(p=0.0, inplace=False)
            )
          )
          (norm2): LayerNorm((320,), eps=1e-05, elementwise_affine=True)
          (attn2): Attention(
            (to_q): Linear(in_features=320, out_features=320, bias=False)
            (to_k): Linear(in_features=768, out_features=320, bias=False)
            (to_v): Linear(in_features=768, out_features=320, bias=False)
            (to_out): ModuleList(
              (0): Linear(in_features=320, out_features=320, bias=True)
              (1): Dropout(p=0.0, inplace=False)
            )
          )
          (norm3): LayerNorm((320,), eps=1e-05, elementwise_affine=True)
          (ff): FeedForward(
            (net): ModuleList(
              (0): GEGLU(
                (proj): Linear(in_features=320, out_features=2560, bias=True)
              )
              (1): Dropout(p=0.0, inplace=False)
              (2): Linear(in_features=1280, out_features=320, bias=True)
            )
          )
        )
      )
      (proj_out): Conv2d(320, 320, kernel_size=(1, 1), stride=(1, 1))
    )
  )

The PyTorch definition of the model lives in diffusers.

Let’s walk through both attn1 (self-attention) and attn2 (cross-attention) for the input tensor - x = [1, 4, H, W]:

  • After conv_in: x becomes [1, 768, H, W]
  • After flattening, x becomes [1, H*W, 768]

The Self-Attention model is defined as follows(simplified):

class Attention(nn.Module):
    def __init__(self):
        self.to_q = nn.Linear(768, 768, bias=False)
        self.to_k = nn.Linear(768, 768, bias=False)
        self.to_v = nn.Linear(768, 768 ,bias=False)
        self.to_out = nn.Sequential(nn.Linear(768, 768), nn.Dropout(0.0))

    def forward(self, x, context=None):
        if context is None:
            context = x  # ← this is self-attention!

        q = self.to_q(x)       # [B, HW, C]
        k = self.to_k(context) # [B, HW, C]
        v = self.to_v(context) # [B, HW, C]

        scale = q.shape[-1] ** -0.5
        sim = torch.matmul(q, k.transpose(-1, -2)) * scale  # [B, HW, HW]
        attn = torch.softmax(sim, dim=-1)

        out = torch.matmul(attn, v)  # [B, HW, C]
        out = self.to_out(out)
        return out

In self-attention,

  • q, k, v all have the shape [1, HW, 768]
  • attn = softmax(q @ kᵀ / √768) → [1, HW, HW]
  • output = attn @ v → [1, HW, 768]
  • Reshape back to [1, 768, H, W] via .permute(0, 2, 1).view(1, 768, H, W)

The Cross-Attention model is defined as follows(simplified):

class Attention(nn.Module):
    def __init__(self):
        self.to_q = nn.Linear(768, 768, bias=False)
        self.to_k = nn.Linear(768, 320, bias=False)
        self.to_v = nn.Linear(768, 320 ,bias=False)
        self.to_out = nn.Sequential(nn.Linear(768, 768), nn.Dropout(0.0))
        
    def forward(self, x, text_embed, mask=None):
        # Project queries from image features
        q = self.to_q(x)  # shape: [B, HW, C]

        # Project keys and values from text_embed
        k = self.to_k(text_embed)  # [B, T_text, C]
        v = self.to_v(text_embed)  # [B, T_text, C]

        # Scaled dot-product attention
        scale = q.shape[-1] ** -0.5
        sim = torch.matmul(q, k.transpose(-1, -2)) * scale  # [B, HW, T_text]

        if mask is not None:
            sim = sim.masked_fill(mask, -float("inf"))

        attn = torch.softmax(sim, dim=-1)  # attention weights
        out = torch.matmul(attn, v)        # [B, HW, C]

        out = self.to_out(out)             # final projection
        return out

Continuing from attn1,

  • The input latent vector has shape: [1, 768, H, W] → flattened to [1, HW, 768]
  • Text embedding (CLIP) has shape: [1, N, 768] (N tokens, N <= 77)
  • q = to_q(x) → [1, HW, 768] from the image latent, where HW = H × W (e.g. 37×37 = 1369)
  • k = to_k(text_embed) → [1, N, 768] from the text embeddings, projected to match inner dimension
  • v = to_v(text_embed) → [1, N, 768] also from the text embeddings
  • attn = softmax(q @ kᵀ / √768) → [1, HW, N] Each image patch (query) attends over N tokens (text prompt length)
  • output = attn @ v → [1, HW, 768] Injects textual semantic information into each image patch
  • Reshape back to [1, 768, H, W] via: .permute(0, 2, 1).view(1, 768, H, W)