PyTorch实现线性回归
Motivation
PyTorch是Facebook开源的一套Deep Learning的框架,它的设计是基于eager execution,因此非常容易上手,对Researcher也非常友好。简单理解,PyTorch是具有自动求导功能的Numpy。
Linear Regression
我们使用的例子是一个很简单的线性回归模型,假设我们有一组观测数据如下
t_y = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_x = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
我们先观察一下数据的分布
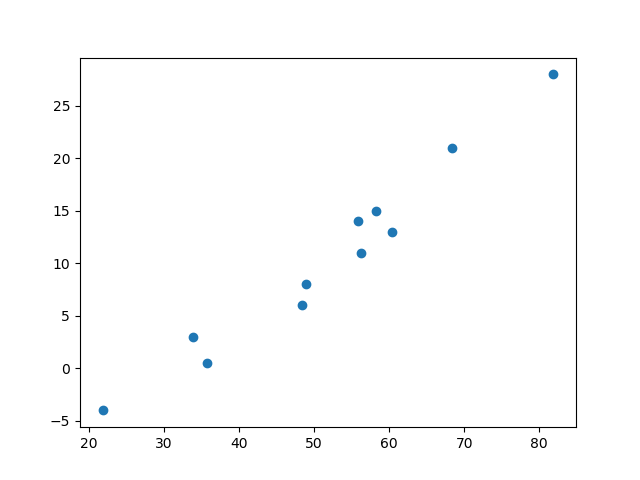
图中可以看出,我们的数据只有一个feature,我们的目标是找到一个线性模型,使下面等式成立
\[t_y = \omega \times t_x + b\]实际上就是对上述的离散点进行线性拟合。我们首先来创建两个tensor
import torch
t_y = torch.tensor(t_y)
t_x = torch.tensor(t_x)
接下来我们来定义我们的model和Loss函数
def model(t_x,w,b):
return w*t_x + b
def loss_fn(t_y, t_p):
squared_diff = (t_y-t_p)**2
return squared_diff.mean()
我们可以先随机生成一组数据,跑一下
w = torch.randn(1)
b = torch.zeros(1)
t_p = model(t_x, w, b)
loss = loss_fn(t_y,t_p) //tensor(2478.7595)
可以看到loss非常大,这样在我们的意料之中,因为我们还没有对model进行训练,接下来我们要做的就是想办法来训练我们的model。由前面机器学习的文章可知,我们需要找到$\omega$,使loss函数的值最小,因此我们需要首先建立loss函数和$\omega$的关系,然后用梯度下降法找到使loss函数的收敛的极小值点,即可得到我们想要的$\omega$的值。$b$的计算同理。以$\omega$为例,回忆梯度下降的公式为
\[w := w - \alpha \times \frac {dL}{d\omega}\]其中$\alpha$为Learning Rate,loss函数对$\omega$的导数,我们可以使用链式求导法则来得到
\[\frac {dL}{d\omega} = \frac {dL}{d\hat y} \times \frac {d\hat y}{d\omega}\]对应到代码中,我们需要定义一个求导函数grad_fn
def dloss_fn(t_y, t_p):
return 2*(t_y-t_p)
def dmodel_dw(t_x,w,b):
return t_x
def dmodel_db(t_x,w,b):
return 1.0
def grad_fn(t_x,w,b,t_y,t_p):
dw = dloss_fn(t_y,t_p) * dmodel_dw(t_x,w,b)
db = dloss_fn(t_y,t_p) * dmodel_db(t_x,w,b)
return torch.tensor([dw.mean(), db.mean()])
有了梯度函数后,我们便可以使用梯度下降接法来训练我们的model了
def train(learning_rate,w,b,x,y):
t_p = model(x, w, b)
loss = loss_fn(y, t_p)
print("loss: ",loss)
w = w - learning_rate * grad_fn(t_x,w,b,t_y,t_p)[0]
b = b - learning_rate * grad_fn(t_x,w,b,t_y,t_p)[1]
t_p = model(x, w, b)
loss = loss_fn(y, t_p)
print("loss: ",loss)
return (w,b)
上面我们先执行了一次forward pass,得到了loss,然后进行了一次backward pass,得到了新的$\omega$和$b$,接着我们又进行了一次forward,又得到了一个新的loss值。我们可以猜想,loss值应该会变小,我们训练一次观察一下结果
train(learning_rate=1e-2,
w=torch.tensor(1.0),
b=torch.tensor(0.0),
x=t_x,
y=t_y)
loss: 1763.8846435546875
loss: 5802484.5
我们发现loss的值没有变小,反而变大了。回忆前面机器学习的文章,出现这种情况,有几种可能,比如learning_rate的值过大,或者没有对输入数据进行normalization。我们先试着改变步长
train(learning_rate=1e-4,
w=torch.tensor(1.0),
b=torch.tensor(0.0),
x=t_x,
y=t_y)
#----------------------------
loss: 1763.8846435546875
loss: 323.0905456542969
我们发现loss的值变小了,符合我们的预期。接着我们尝试对输入数据进行normalization
t_xn = t_x * 0.1
train(learning_rate=1e-2,
w=torch.tensor(1.0),
b=torch.tensor(0.0),
x=t_xn,
y=t_y)
#----------------------------
loss: 80.36434173583984
loss: 37.57491683959961
这里我们可以使用更复杂的normalization方法,这里为了简单起见,直接领输入数据乘以0.1
通过一系列操作,loss已经可以收敛了,这说明我们的梯度下降可以正常工作,接下来我们便可以正式训练了,我们对上面代码稍微重构一下
def train_loop(epochs, learning_rate, params, x, y):
for epoch in range(1, epochs + 1):
w,b = params
t_p = model(x, w, b)
loss = loss_fn(y, t_p)
grad = grad_fn(x,w,b,y,t_p)
params = params - learning_rate * grad
print(f'Epoch: {epoch}, Loss: {float(loss)}')
return params
param = train_loop(epochs = 5000,
learning_rate = 1e-2,
params = torch.tensor([1.0,0.0]),
x = t_x,
y = t_y)
print("w,b",float(param[0]), float(param[1]))
#----------------------------
Epoch: 1, Loss: 80.36434173583984
Epoch: 2, Loss: 37.57491683959961
...
Epoch: 4999, Loss: 2.927647352218628
Epoch: 5000, Loss: 2.927647590637207
#----------------------------
w,b 5.367083549499512 -17.301189422607422
我们循环了5000次,loss收敛在2.927647左右,不再下降,此时我们可以认为得到的$\omega$和$b$是我们最终想要的,为了更直观的理解,我们将训练得到模型画出来,其中黄色的点为我们原始离散数据点,蓝色的线是我们训练好的model,即拟合出来的曲线
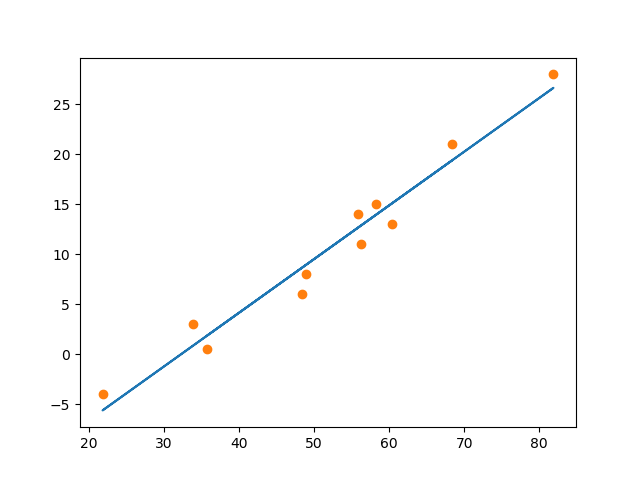
Autograd
上述代码并没有什么特别的地方,我们手动的实现了对$\omega$和$b$的求导,但由于上面的model太过简单,因此难度不大。但是对于复杂的model,比如CNN的model,涉及到大量的待学习的参数,如果纯用手动求导的方式则会非常复杂,且容易出错。正如我前面所说,PyTorch强大的地方在于不论model多复杂,只要它满足可微分的条件,PyTorch便可以自动帮我们完成求导的计算,即所谓的autograd。
简单来说,对所有的Model,我们都可以用一个Computational Graph来表示,Graph中的每个节点代表一个运算函数
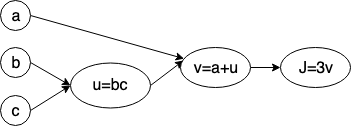
如上图中的a,b,c为叶子节点,在执行forward pass的时候,PyTorch会记住(record)非叶子节点上的函数,保存在该节点对应的tensor中,这样当做backward pass的时候便可以很方便的使用链式求导快速计算出叶子节点的导数值。
a = torch.tensor(3.0, requires_grad=True)
b = torch.tensor(5.0, requires_grad=True)
c = torch.tensor(8.0, requires_grad=True)
这里我们定义了a,b,c三个tensor,并且告诉PyTorch需要对它们进行求导,接下来我们建立Computation Graph
u = b*c
v = a+u
j = 3*v
接下来我们可以验证下每个节点上都有什么信息
>>> u
tensor(40., grad_fn=<MulBackward0>)
>>> j
tensor(129., grad_fn=<MulBackward0>)
>>> v
tensor(43., grad_fn=<AddBackward0>)
可以看到每个节点上的值都被求出来了,也就是PyTorch中所谓的eager mode,另外这几个tensor上面都有grad_fn,用来做autograd。上面的图中,j是最终节点,我们可以让j做backward(),则它会触发u和v做反向求导,而求导的结果会存放在a,b,c上
j.backward()
>>> a.grad
tensor(3.)
>>> b.grad
tensor(24.)
>>> c.grad
tensor(15.)
>>> u.grad #none
>>> v.grad #none
>>> j.grad #none
上面代码中我们用grad函数查看tensor上的导数值,可见只有leaf节点才会累积求导的结果,中间节点不会保存任何中间结果。
关于Autograd详细的实现建议阅读源码,后面如果有时间我们可以写一篇文章专门分析
接下来我们可以用PyTorch的autograd API重写上一节的训练代码
# use autograd
params = torch.tensor([1.0,0.0], requires_grad=True)
def train_loop(epochs, learning_rate, params, x, y):
for epoch in range(1, epochs + 1):
if params.grad is not None:
params.grad_zero()
w,b = params
t_p = model(x, w, b)
loss = loss_fn(y, t_p)
loss.backward() #autograd
params = (params - learning_rate * params.grad).detach().requires_grad_()
print(f'Epoch: {epoch}, Loss: {float(loss)}')
return params
params = torch.tensor([1.0,0.0], requires_grad=True)
param = train_loop(epochs = 5000,
learning_rate = 1e-2,
params = params,
x = t_xn,
y = t_y)
print("w,b",float(param[0]), float(param[1]))
Optimizers
之前机器学习的文章中,我们曾提到过对传统梯度下降的优化,例如当数据量大时,可以使用Stochastic Gradient Descent(SGD),另外还有些优化算法可以帮助我们加快梯度下降的收敛速度,从而减少训练时间。PyTorch内部提供了一系列优化算法的API
import torch.optim as optim
dir(optim))
#----------------------------
['ASGD', 'Adadelta', 'Adagrad', 'Adam', 'AdamW', 'Adamax',
'LBFGS', 'Optimizer', 'RMSprop', 'Rprop', 'SGD', 'SparseAdam',
'__builtins__', '__cached__', '__doc__', '__file__', '__loader__',
'__name__', '__package__', '__path__', '__spec__', 'lr_scheduler']
Optimizer通常和autograd配合使用,因为在训练的时候它需要修改tensor的梯度值,因此Optimizer内部会retain传入tensor。使用Optimizer的方式也很简单,它提供两个API,一个是zero_grad()用于清空tensor上保存的导数值,另一个是step()用来实现具体的optimize的操作。接下来我们为上面的demo引入一个optimizaer
params = torch.tensor([1.0,0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params],lr=learning_rate)
接下来我们需要在backward()执行完成后,调用step()方法来更新params中的值。另外由于optimizer提供了zero_grad()的方法,我们可以将上面手动清除导数值的方式替换成使用zero_grad()方法
def train_loop(epochs, learning_rate, params, x, y):
for epoch in range(1, epochs + 1):
optimizer.zero_grad() #clear grad value on params
w,b = params
t_p = model(x, w, b)
loss = loss_fn(y, t_p)
loss.backward()
optimizer.step() #update params
params = (params - learning_rate * params.grad).detach().requires_grad_()
print(f'Epoch: {epoch}, Loss: {float(loss)}')
return params
重新训练我们model,观察结果发现和前面的结果一致。此外如果将SGD改为Adam,则loss函数的收敛速度会加快,4000次即可达到稳定状态。
小结
发现到目前为止,我们已经使用PyTorch使用优化了我们的训练代码,回过头来总结一下可以发现PyTorch帮我们解决了两大块重要的工作,一个是自动求导,只需要一行backward方法即可,解放了我们的双手。另一个是提供通用的Optimizer,Optimizer的好处是将算法抽象了出来,通过直接mutate训练过程中间节点的信息达到优化参数的目的,从而不需要破坏training loop,使代码逻辑保持清晰。
