The Transformer Block
The Transformer Block
In the previous post, we took a deep dive into the self-attention mechanism. Interestingly, the attention modules contribute only about 1/3 of the model’s total parameters. The remaining 2/3 reside in the feed-forward network layers, also known as the MLP. Besides MLP, other key elements play essential roles within each transformer block — most notably, layer normalization and skip connections, both of which are critical to the model’s stability and performance. In this post, we’ll explore these components in detail.
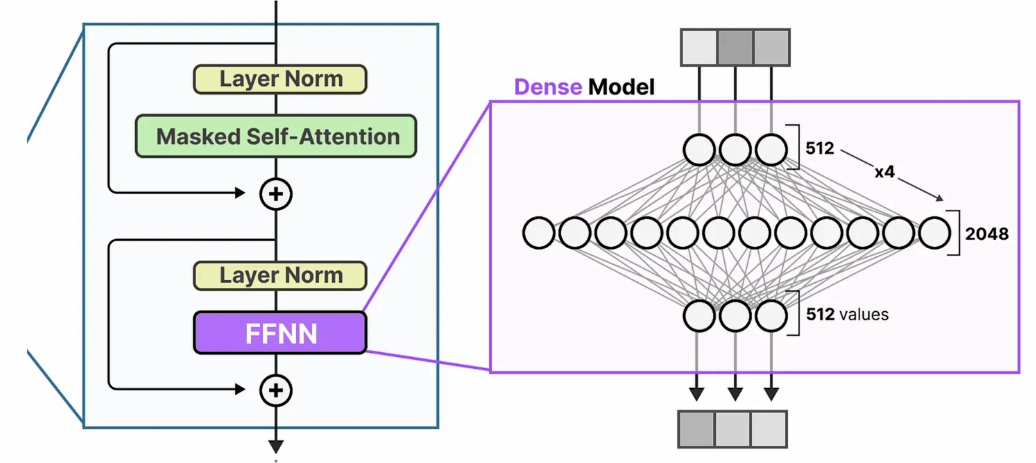
Multi-Layer Perceptron (MLP)
In the last section of the transformer architecture post, we examined the Microsoft’s Phi-3-mini-4k-instruct model. In this section, we will continue using this model as our running example to illustrate how mlp works.
Previously, we saw that the output of an attention head is an attention-enhanced embedding, denoted as $\vec{E_i}$(3072 dimensions). Our next step is to pass $\vec{E_i}$ through a sequence of linear transformations:
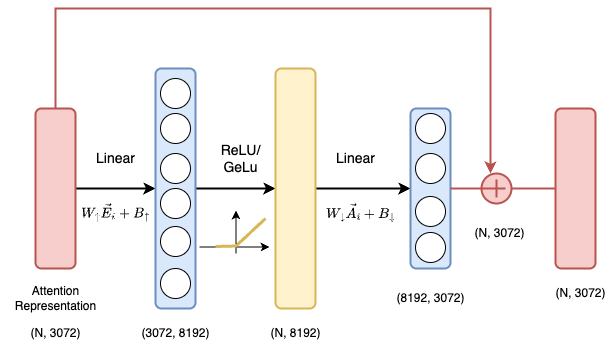
- The first linear layer is an “up projection” matrix: $W_{\uparrow}$, projecting the input from
3072dimensions to8192. - The second linear layer is a “down project” matrix: $W_{\downarrow}$, projecting the activation back to the
3072dimensions. - There is a residual connection at the end that adds the input embeddings to the transformed embeddings
As you can see, the MLP architecture looks quite straightforward. It is just a plain neural network. You may wonder how does it work? Frankly speaking, it is hard to say. The original paper - Attention is All You Need does not explain the reason in detail. However, since MLP is just two linear layers stacked together, we could gain some high-level intuition:
- Non-Linear Feature Transformation: After the self-attention mechanism captures contextual relationships between tokens, the MLP applies a non-linear transformation to each token’s representation independently. This allows the model to learn complex patterns within individual token embeddings that aren’t captured by attention alone.
- Complementing Self-Attention: Self-attention focuses on inter-token relationships (e.g., how words relate to each other in a sentence). Whereas, MLP focuses on outer-token relationships (e.g., transforming the features of a single token into a richer representation). Together, they create a balance between global context and local feature processing.
Layer Normalization
We’ve previously explored the role of BatchNorm in regular neural networks, where its main purpose is to stabilize training. In the transformer blocks, Layer Normalization serves a similar purpose - it scales and shifts the activations of a layer to have zero mean and unit variance (or similar properties) for each token independently.
In other words, Without normalization, small changes in input distributions across layers can amplify (a problem called internal covariate shift), leading to unstable gradients and slower training. Normalization ensures activations stay in a stable range.
In the Phi3 model, Phi3RMSNorm is used, which normalizes by the root mean square (RMS) instead of the standard mean/variance (simplifying computation while retaining benefits).
In each transformer block, we’ll usually see normalization applied:
- Before attention (input layer norm)
- Before MLP (post-attention layer norm)
- After the final transformer block (final norm before LM head)
It’s worth noting that unlike batch normalization, which normalizes across the batch dimension, layer normalization operates per token. This makes it ideal for transformers:
- Works seamlessly with variable-length sequences (common in NLP tasks).
- Avoids instability when batch sizes are small or vary (batch normalization struggles here)
Skip Connections
Originally, skip connections(residual network) was first introduced in ResNet in the computer vision world to mitigate the challenge of vanishing gradients when training deep CNN models. In the transformer block, the goal is the same - to let gradient flow through the network by skipping one or more layers, which is achieved by adding the output of one layer to the output of a later layer.
In the transformer block, the residual connections are used in two places:
- After self-attention:
# pseudo code
attn_output = self_attn(input_layer_norm(x)) # Apply self-attention to normalized input
x = x + resid_attn_dropout(attn_output) # Residual connection
- After MLP:
# pseudo code
mlp_output = mlp(post_attention_layernorm(x)) # Apply MLP to normalized post-attention output
x = x + resid_mlp_dropout(mlp_output) # Residual connection
Note that, in practice, we add dropout to the residual path acts as a regularization item. It randomly zeros out parts of the sub-layer’s output during training, forcing the model to:
- Avoid over-relying on specific neurons
- Learn redundant/robust features
The Transformer Block in practice
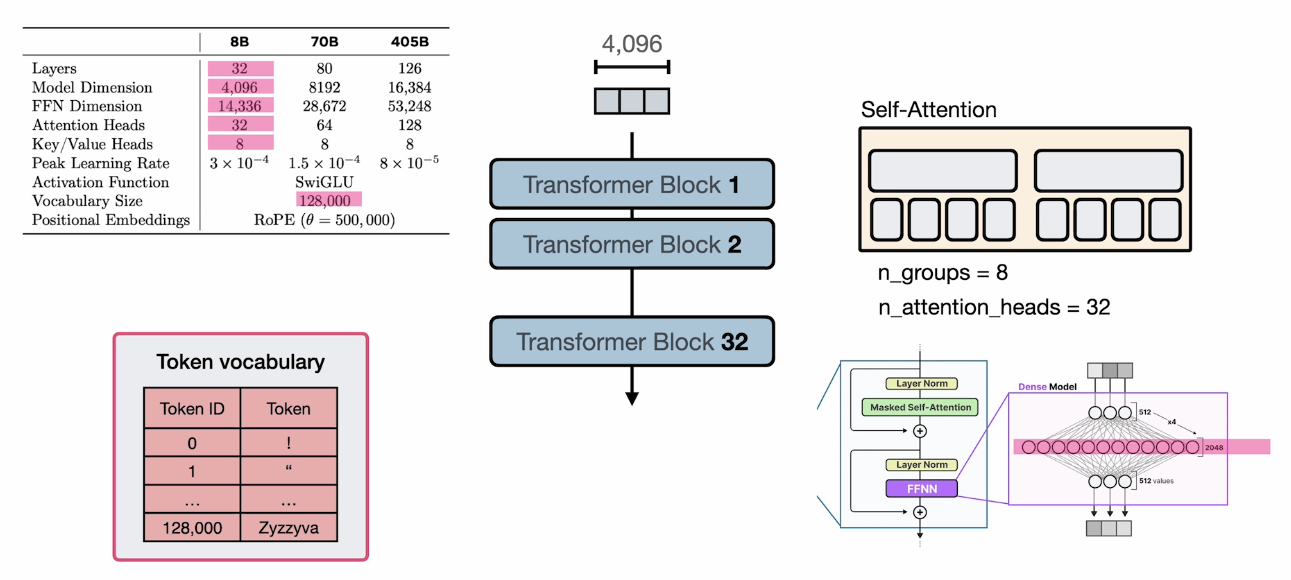
Now, let’s continue our discussion on the Meta’s Llama3 architecture. In the previous post, we analyzed the attention modules. Now that we understand what the transformer block means, we can piece everything together.
Based on the numbers in the paper, the 8B model contains:
32transformer blocks/layers- Each transformer block contains
- 32 attention heads grouped by 8 key/value heads (8 groups, 8 different key/value matrices, 32 query metrics)
- A MLP layer that project the embedding to
14,336dimension
- The vocabulary dictionary size is
128,000 - Each embedding vector has
4096dimensions
